ПОРСПЕКТИВА ПРЯМОЙ ЛИНИИ

ЛЕКЦИЯ 5

Содержательный модуль4 Линейная перспектива

Тема: Центральное проецирование. Линейная перспектива точки и прямой линии

Изучаемые вопросы:

1. Основные понятия

2. Аппарат линейной перспективы

3. Перспектива точки

4. Перспектива прямой линии

5. Выбор точки зрения

6. Перспективные масштабы

 

ОСНОВНЫЕ ПОНЯТИЯ

Перспективой называется изображение предметов построенное методом центрального проецирования с учетом закономерностей и особенностей зрительного восприятия человеком окружающего пространства.

Перспективное изображение сооружения можно получить если перед сооружением поставить прозрачную плоскость (стекло) и по стеклу обвести краской видимые контуры сооружения. Изображение на стекле и будет перспективным.

Название «перспектива» от латинского слова perspisere, что в переводе означает «смотреть сквозь, правильно видеть».

Различают геометрическую, воздушную, аналитическую и другие виды перспектив.

К геометрической перспективе относятся:

- линейная перспектива – изображение на плоскости;

- панорамная перспектива – изображение на внутренней поверхности цилиндра;

- купольная перспектива – изображение на внутренней поверхности сферы (шара).

Линейная перспектива изучает способы построения перспективных изображений линий контура предметов на плоскости. При этом плоскость проекций чаще выбирают вертикальной (рис.1).

 

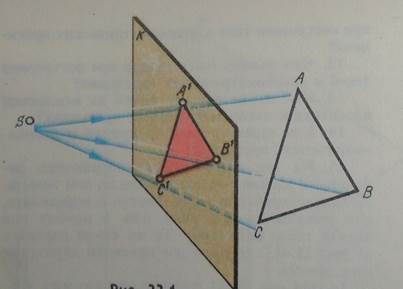
Рисунок 1

 

АППАРАТ ЛИНЕЙНОЙ ПЕРСПЕКТИВЫ

Для построения перспективного изображения пользуются аппаратом центрального проецирования – системой плоскостей, линий и точек (рис.2).

Рисунок 2

Основными элементами аппарата проецирования являются:

- предметная плоскость П, на которой расположен изображаемый предмет;

- картинная плоскость (картина) К, вертикальная плоскость, которая расположена между наблюдателем и объектом изображения перпендикулярно к предметной плоскости;

- точка S – точка зрения, она определяет положение глаза наблюдателя относительно картины и предметной плоскости;

- точка S₁ – точка стояния (основание точки зрения) – основание перпендикуляра, опущенного из точки S на плоскость П;

- длинна перпендикуляра S S₁ – высота точки зрения;

- точка Р – главная точка картины, которая является прямоугольной проекцией точки зрения на картинную плоскость;

- зрительное расстояние – длинна перпендикуляра SР (расстояние от наблюдателя до картины);

- точки D¹ и D² - дистанционные точки, которые показывают зрительное расстояние Р D¹=Р D²= SP);

- линия КК_! – основание картины (линия пересечения предметной плоскости и картинной плоскости;

- плоскость горизонта ẞ - плоскость проведенная через точку S параллельно предметной плоскости;

- нейтральная плоскость – плоскость которая проходит через точку S параллельно картинной плоскости;

- картинная и нейтральная плоскости разделяют все пространство на три части: предметное – за предметной плоскостью, нейтральное – между картиной и нейтральной плоскостью и мнимое – за наблюдателем;

- линия hh₁ – линия горизонта, которая является линией пересечения плоскости горизонта с картинной плоскостью и проходит через главную точку картины Р параллельно основанию картины.

 

ПЕРСПЕКТИВА ТОЧКИ

Перспективой точки (центральной проекцией точки на картинную плоскость) называют точку пересечения с картинной плоскостью проекционного луча направленного из центра проекций к точке. Однако эта проекция не определяет положение точки в пространстве, так как все точки, которые лежат на проекционном луче, спроецируются в одну точку. Потому кроме перспективы заданной точки, необходимо построить на картине еще и перспективу ее горизонтальной проекции – основания.

Чем ближе точка к плоскости, тем перспектива ее основания больше отдалена от линии горизонта. Перспектива основания точки, находящейся в бесконечности за картинной плоскостью, будет находиться на линии горизонта.

Положение точки в пространстве проекционного аппарата определяется на картине расположением перспективы точки и перспективы ее основания.

Пусть в предметном пространстве задана произвольная точка В¹ и ее ортогональная проекция b¹ на предметную плоскость (рис.3, а). Построим перспективу точки В¹. Проведем из точки зрения S луч в точку В¹, тоесть S В¹. Построим проекцию sb прямой SВ¹. Поместим прямые SВ¹ и sb¹ в горизонтально-проецирующую плоскость Q. Эта плоскость пересекается с картинной плоскостью пог прямой О₂Т, которая расположена перпендикулярно основанию картины ОО_1. Перспектива точки В¹ и ее основания b¹ лежат на прямой О₂Т (рис. 3, б).

Если точка В¹ лежит на предметной плоскости Н, то ее ортогональная проекция b¹ совпадает с самой точкой В¹ (Рис.4). На картине перспектива точки В¹ совпадает с ее основанием тоесть В = b.

 

 

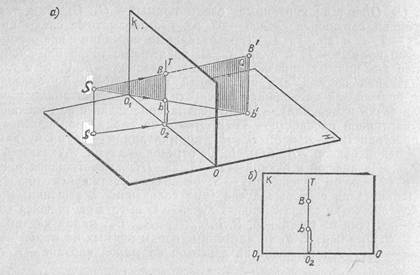
Рисунок 3

 

Рисунок 4

ПОРСПЕКТИВА ПРЯМОЙ ЛИНИИ

Перспективу прямой линии можно строить если представить плоскость, которая состоит из прямых, выходящих из точки зрения S к каждой точке заданной прямой. Линия пересечения этой плоскости с картиной есть прямая. Тоесть, перспектива прямой на картине есть прямая. Для получения перспективы прямой достаточно построить перспективу двух ее точек.

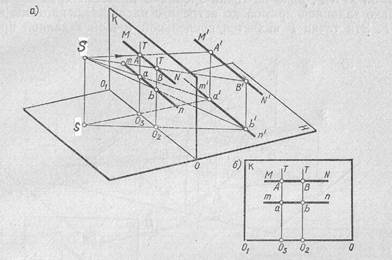
Предположим, что в пространстве находится некоторая прямая М¹N¹, которая расположена параллельно картине и предметной плоскости (рия. 5, а). Для построение перспективы прямой М¹N¹, возьмем на ней две произвольные точки А¹ и В¹ и найдем их ортогональные (горизонтальные) проекции a¹, b¹ (ортогональные проекции точек на предметную плоскость Н называются основаниями этих точек). Перспективу точек А¹ и В¹

Рисунок 5

определяем с помощью плоскостей SA¹sa¹ та SB¹sb¹, линии пересечения которых с картинной плоскостью являются прямые О₃Т и О₂Т перпендикулярные основанию картины ОО₁. Перспективы точек А¹ и В¹ находятся на пересечении прямых SA¹ и SB¹ с прямыми О₃Т и О₂Т. Соединив прямой точки А,В и a,b, получим перспективу прямой А¹ В¹ и ее проекции a¹ b¹. Полеченная перспектива отрезка А¹ В¹ на картине уменьшилась и расположилась параллельно основанию картины (рис.6, б).

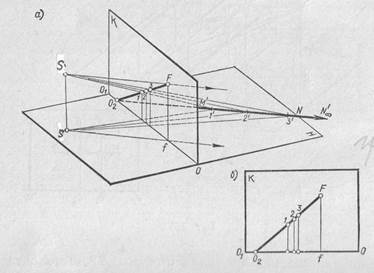
Рассмотрим построение перспективы прямой, идущей в бесконечность. Если в предметной плоскости взять некоторую прямую и продолжить ее в бесконечно далеко от наблюдателя, то перспектива бесконечно удаленной точки заданной прямой называется граничной точкой прямой. Для получения перспективы граничной точки прямой возьмем на прямой MN, лежащей в предметной плоскости Н (рис.6) две произвольные точки 1¹ и 2¹ и построим их перспективу. Из построения видно, что точка 1¹ расположена ближе к наблюдателю чем точка 2¹, поэтому на картине точка 1 расположилась ниже точки 2. На этой же прямой возьмем еще одну точку 3¹, которая удалена от наблюдателя больше чем точка 2¹, и построим ее перспективу. Перспектива точки 3¹ – точка 3 расположилась на картине выше чем точки 1 и 2. Если продолжить прямую M¹N¹ дальше и взять на ней ряд других точек, то перспективы этих точек на картине расположатся еще выше. Таким образом, чем дальше от наблюдателя точка, тем выше она располагается на картине. Для того, чтобы построить перспективу бесконечно удаленной точки на прямой M¹N¹_∞, нужно из точки зрения S провести прямую параллельно заданной прямой до встречи с картинной плоскостью в точке F. Эта точка будет граничной точкой заданной прямой. И так, перспектива бесконечно удаленной точки прямой M¹N¹_∞ , расположена на пересечении прямой SF, проведенной параллельно заданной прямой с плоскостью картины. Граничная точка всегда удалена от основания картины ОО₁ на расстояние, равное высоте точки зрения Ss.

Рисунок 6

 

Продолжаем прямую M¹N¹ до пересечения с картиной в точке О₂. Точку О₂ встречи прямой с картиной называют картинным следом. Соединив картинный след О₂ с точкой F,, получаем на картине перспективу прямой M¹N¹_∞ (рис.6, б).

Если взять на предметной плоскости две произвольно расположенные прямые А¹А¹_∞ і В¹В¹_∞ (рис.7, а) и построить на картине их граничные точки F и F₁ то обе точки расположатся на одинаковом расстоянии от основания картинны ОО₁ ,которое равно высоте точки зрения.

Рисунок 7

На предметной плоскости можно взять множество прямых произвольно направленных, идущих в бесконечность (Рис. 7, б), граничные точки для каждой из них расположатся на линии hh_1, параллельной основанию картины ОО₁ . Эта линия и есть линией горизонта или горизонтом.

Для пучка параллельных прямых, расположенных в предметной плоскости и параллельных ей, существует одна общая граничная точка. Действительно, если наблюдать за железнодорожными рельсами, которые идут вдаль, то можно увидеть, что с отдалением расстояние между ними уменьшается и рельсы видятся сходящимися в одной точке. Точно так все объемные предметы, которые нас окружают, видятся нами с перспективным уменьшением. Это обусловлено строением глаза человека. Поэтому, когда художник рисует предметы, он изображает их такими, какими видит в натуре, тоесть с перспективным уменьшением.

Рассмотрим построение перспективы параллельных прямых. Возьмем на предметной плоскости две параллельные прямые А¹А_∞¹ и В¹В_∞¹, перпендикулярные картине и идущие в бесконечность (рис.8). Продолжим прямые до пересечения с основанием картины и определим их картинные следы О₂ и О₃. Проведем луч зрения из точки S параллельно заданным прямым и определим граничную точку Р. Очевидно, что для двух параллельных прямых граничная точка одна. Построим перспективу каждой прямой на картине. Для этого соединим картинные следы О₂ и О₃ с граничной точкой Р. На картине перспектива двух параллельных прямых выходит в виде двух прямых, сходящихся в одной точке Р. Точка Р является граничной точкой для всех прямых, параллельных прямым А¹А_∞¹ и В¹В_∞¹, расположенных между предметной плоскостью и плоскостью горизонта. И так, если прямые в пространстве параллельны, то перспективы их проходят через одну общую точку схода.

Рисунок 8

Для параллельных прямых, расположенных перпендикулярно картине, точкой схода всегда будет точка Р – главная точка картины.

И так, при построении перспективы прямых необходимо помнить, что:

ü Построение перспективы отрезка прямой линии сводится к построению перспективы двух его точек;

ü В общем случае перспективой прямой является прямая линия, но если прямая совпадает с проекционным лучом, то перспективой прямой будет точка;

ü Концом перспективы бесконечно продолженной прямой, которая лежит в предметной плоскости, как и любой горизонтальной прямой предметного пространства, является граничная точка (точка схода), которая лежит на линии горизонта картины;

ü Линия горизонта – граничная прямая предметной плоскости которая проходит на картине на высоте центра проекций (уровня глаз) параллельно основанию картины. Ее можно рассматривать также как границу перспективы продолженной в бесконечность предметной плоскости предметного пространства;

ü Прямые в предметном пространстве могут располагаться относительно предметной и картинной плоскостей по разному (прямая общего положения расположенная под произвольным углом к этим плоскостям, прямые частного положения – параллельные или перпендикулярные к предметной или картинной плоскостям);

ü Различают восходящие и нисходящие прямые общего положения. Восходящими называют прямые предметного пространства, направленные снизу вверх с одновременным отдалением их точек от картинной и предметной плоскостей. Нисходящие прямые направлены сверху вниз, их точки приближаются к предметной плоскости, удаляясь от картины.

ü Горизонтальные прямые, параллельные картинной плоскости изображают на картине горизонтальными, вертикальные – вертикальными;

ü Прямые линии в предметном пространстве могут быть между собой параллельными и скрещивающимися. Перспективы параллельных прямых на картине пересекаются в одной точке схода.

ВЫБОР ТОЧКИ ЗРЕНИЯ

Для художника, который работает над перспективным изображением любого объекта, важным является передача зрителю правильного, тоесть реалистичного изображения его формы, размеров и пропорций. Для этоговыбор высоты линии горизонта, расстояние зрителя от картины и положение точки зрения не должны быть случайными.

Когда художник смотрит в одном направлении, его глаз охватывает пространство, которое ограничено лучами зрения. Лучи света, отражаясь от видимых предметов, направляются в глаз и сходятся в зрачке. Таким образом, совокупность световых лучей, которые идут под определенным углом в глаз человека, создает коническую поверхность. При пересечении этой поверхности с картиной в сечении образуется замкнутая кривая, которая ограничивает поле зрения. Полем зрения называется фигура, которая получается в результате пересечения конуса, который образуется лучами зрения с плоскостью, которая направлена перпендикулярно главному лучу зрения. Строение глаза человека таково, что он охватывает в ширину большее пространство, чем в высоту. У;гол, образующийся двумя крайними лучами зрения, которые ограничивают видимое пространство в любой плоскости, которая пересекает конус, называется углом зрения. Угол зрения вверх от главного луча составляет 45° и к низу 65°. Каждый из боковых углов зрения равняется приблизительно 70°, тоесть боковой охват угла зрения равен 140°.

Наиболее ясно человек модет видеть только в небольшой центральной части поля зрения, которая называется полем ясного зрения. Иначе говоря, человеческий глаз может заметить присутствие предмета, который расположен в периферийной точке поле зрения, но для того, чтобы различить детали, предмет должен разместиться в поле ясного зрения. Поле ясного зрения определяется углом в 28° при отдалении точки зрения от картины приблизительно на удвоенную высоту. Натура тоже должна находиться в пределах ясного поля зрения, тоесть художник должен стоять или сидеть на расстоянии в два раза большем высоты от нее. Для построения изображения отдельных предметов и композиций на открытом пространстве принято выбирать угол в пределах 28-37°, а для построения перспективы интерьеров – до 53°. На основании этого, картина всегда должна вписываться в поле зрения, не зависимо от формы. Если размер диагонали картины удвоить, то получим угол зрения, приблизительно 28°. Поэтому на картине дистанционные точки D и D₁ должны располагаться от точки Р на расстоянии двух ее диагоналей.

ПЕРСПЕКТИВНЫЕ МАСШТАБЫ

Предметы, окружающие челове6ка в пространстве, имеют три измерения: глубину, ширину и высоту. При построении перспективы разных фигур используются перспективные масштабы. Перспективные масштабы позволяют выполнять на картинной плоскости перспективные изображения не только плоских, но и объемных фигур. В перспективе, тоесть на картине, изображаются не действительные размеры предметов, а только их пропорциональные отношения. Поскольку отрезки, которые лежат на картине, совпадают со своими проекциями, то за натуральные размеры отрезков берем отрезки, которые расположены на плоскости картины. Натуральные размеры отрезков размещают на основании картины и ее боковых сторонах. В предметном пространстве измерения можно выполнять по трем направлениям: перпендикулярно картинной плоскости (глубина); параллельно основанию картины (ширина); перпендикулярно предметной плоскости (высота).

Масштаб глубины, это масштаб построенный на прямой, которая перпендикулярна картине. На картине задана перспектива точки А, которая расположена на прямой О₂Р (рис. 9). Необходимо от точки А отложить отрезок АВ, равный отрезку L. Для лучшего понимания сути построения, обратимся к решению этой задачи, построенной натурально по правилам геометрии (рис.9, б). Начертим две перпендикулярные прямые, которые пересекаются в точке 1. На вертикальной прямой возьмем точку А. Рядом с горизонтальной прямой начертим отрезок L. Через точку А проведем прямую под углом 45° к горизонтальной прямой до пересечения ее в точке 2. От точки 2 отложим вправо отрезок 2-3, равный L. Через точку 3 проведем прямую, параллельную прямой 2-А до пересечения с вертикальной прямой в точке В. Отрезок АВ равный отрезку 2-3, потому что оба отрезка лежат на сторонах прямого угла и расположены на одном расстоянии от его вершин.

Рисунок 9

Построение перспективы отрезка АВ, равного L, выполняем по такому же принципу. Через точку А и D₁ проведем прямую до пересечения с основанием картины в точке О₃ (рис.9, в), тоесть прямую О₃D₁ под углом к картине. 45°. От точки О₃ вправо на основании картины откладываем отрезок О₃-О₄,равный отрезку L. Через точку О₄ проведем прямую в точку D₁ . Прямая О₄D₁ пересекается с прямой О₂Р в точке В. Отрезок АВ равен отрезку О₃О₄ и отрезку L. Этот способ позволяет выполнять обратную задачу, тоесть измерять перспективу отрезка по заданному линейному масштабу. На картине задана перспектива отрезка АВ (рис.10). Необходимо измерять его размер, используя для этого линейный масштаб (0, 1, 2, 3, 4). Через концы отрезка АВ проведем прямые в точку D и продолжим прямые до пересечения с основанием картины в точках О₄ і О₃. Отрезок О₄О₃ и есть размер отрезка АВ. Измеряв отрезок О₄О₃ по линейному масштабу, получим размер отрезка АВ в масштабе.

Рисунок 10

Масштаб ширины, это масштаб построенный на прямой, расположенной параллельно основанию картины. На основании картины возьмем произвольный отрезок О₂О₃ заданной длины (рис.11, а). Соединим концы отрезка с точкой Р. Получим две параллельные прямые, перпендикулярные основанию картины. На прямой О₂Р возьмем произвольную точку А и проведем через нее прямую, параллельную основанию картины. Прямая пересечет прямую О₃Р в точке В. Перспектива отрезка АВ равна отрезку О₂О₃ по масштабу ширины, потому что фигура О₂АВО₃ является перспективой прямоугольника. И так, отрезки, которые проведены между параллельными прямыми О₂Р и О₃Р параллельно основанию картины, все равны между собой.

Перспективный масштаб ширины сохраняется и для параллельных прямых, проведенных через произвольную точку схода F. В этом случае фигура О₄ЕQО₅ является перспективой параллелограмма. На рисунке 10, б показано тоже построение в натуре по правилам геометрии.

Масштаб высоты, это масштаб построенный на прямой, перпендикулярной предметной плоскости.

Возьмем на основании картины произвольную точку О₂ (рис.12) и поднимем из нее перпендикуляр до основания картины О₂А. Через точки О₂ и А проведем две параллельные прямые в произвольную точку схода F. Очевидно, что любой отрезок,

 

Рисунок 11

проведенный параллельно отрезку О₂А между параллельными прямыми АF и О₂F, равен отрезку О₂А.

 

Рисунок 12

При решении задач необходимо помнить:

1. В построении перспективных изображений геометрических фигур нужно знать их взаимное расположение, размеры и расстояния между ними, тоесть уметь решать позиционные и метрические задачи;

2. Метрическими называют задачи на построение фигур заданной величины, определение действительной величины отрезков, углов и плоских фигур;

3. Решение метрических задач связано с выполнением измерений, вследствие которых возникает необходимость выяснения соотношений между действительными и перспективными линейными размерами изображаемых объектов. Поэтому нужно знать масштаб картины – единицу длины линейного масштаба картины, тоесть масштаб отрезков, которые расположены в картинной плоскости)масштаб на рамке картины).

4. На картине объекты изображаются в трех измерениях с учетом возможного расположения их в глубину предметного пространства. Поэтому тут удобнее пользоваться перспективным масштабом, который состоит из линейных масштабов трех взаимно перпендикулярных главных направлений: ширины, высоты и глубины;

5. Масштаб, построенный на прямой, параллельной основанию картины, называют масштабом ширины. Чтобы построить действительную величину отрезка, расположенного на картине параллельно ее основанию, нужно выбрать на линии горизонта любую точку схода линий переноса и из этой точки провести прямые через концы отрезка до пересечения с основанием картины в точках, расстояние между которыми и будет искомой;

6. Масштаб, построенный на прямой, перпендикулярной к предметной плоскости, называют масштабом высоты. Чтобы построить действительную величину перспективы вертикального отрезка, нужно провести через перспективу отрезка вспомогательную плоскость и с граничной точки предметного следа этой плоскости провести прямые через концы перспективы отрезка до пересечения с картинным следом вспомогательной плоскости в точках, расстояние между которыми и будет искомой;

7. Масштаб, построенный на прямой, перпендикулярной к картинной плоскости, называют масштабом глубины. Точки схода горизонтальных прямых, направленных слева на право и справа налево, до плоскости картины под углом 45°, называют дистанционными точками. На картине по дистанционным точкам можно строить совмещенную точку зрения и, наоборот, по совмещенной точке зрения можно построить дистанционные точки. Расстояние от главной точки картины до совмещенной точки зрения равно расстоянию от центра проекций до картины. Чтобы построить действительную величину перспективы глубинного отрезка, нужно провести прямые с дистанционной точки (правой или левой) через концы глубинного отрезка до пересечения с основанием картины;

8. Масштаб, построенный на произвольной прямой, называют перспективным масштабом для прямых общего положения. В этом случае используется масштабная точка, из которой проводят прямые через концы отрезка до пересечения с картиной.