Тема. Параллельное проектирование.
Методические рекомендации
Пусть дано произвольную плоскость α,
точка А (рис. 83) и прямую h, которое пересекает плоскость α. Проведем через точку А прямую, которая параллельна h, она пересекает плоскость α в некоторой точке А1. Найденную таким образом точку А; называют параллельной проекцией точки А на плоскость α в направлении h. Прямую h называют
проектирующей прямой, плоскость α - плоскостью проекций.

Чтобы построить проекцию какой-либо фигуры, надо спроектировать на плоскость проекции каждую точку данной фигуры (рис. 84). Приведем некоторые свойства параллельного проектирования.

Теорема. Если отрезки, которые проектируются, не параллельны проектирующей прямой, то при параллельном проектировании:
Свойства параллельного проектирования:
1) отрезки изображаются отрезками;
2) параллельные отрезки изображаются параллельными отрезками или отрезками одной прямой;
3) отношение длин параллельных отрезков и отрезков одной прямой сохраняется.
Доказательство:
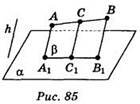
1)1) Все прямые, которые проектируют точки отрезка АВ лежат в одной плоскости β, которая пересекает плоскость α по прямой А1В1 (рис. 85). Следовательно, проекцией отрезка есть отрезок, причем произвольная точка С отрезка АВ изображается точкой С1 отрезка А1В1.
2) Пусть отрезки АВ и CD, которые проектируются, параллельные. Все прямые, которые их пересекают и параллельные h, заполняют или части одной плоскости (рис. 86), или параллельных плоскостей (рис. 87).


Эти части плоскостей пересекают плоскость а соответственно или по отрезкам одной прямой, или по параллельным отрезкам А1В1 и С1D1.
3) Если отрезки АВ и СВ, которые проектируют, размещены на одной прямой (см. рис. 85), то по теореме о пропорциональных отрезках имеем: А1С1: С1B1 = АС: СВ.
Если отрезки АВ и CD параллельны, а их проекции А1В1 и С1D1лежат на одной прямой (см, рис. 86), то АВВ2 A2 - параллелограмм. В этом случае А1В1: С1D1 = A2B2: CD = AB: CD. Наконец, если проекции А1В1 и С1D1 данных отрезков АВ и CD не лежат на одной прямой (см. рис. 87), то построим параллелограмм CDKB. Его проекция - параллелограмм СDKВ. Итак, имеем: А1В1: С1D1 = А1В1 : В1К1 = АВ: ВК = АВ: CD.
Изображение пространственных фигур на плоскости
Приведем примеры изображений пространственных фигур на плоскости. Изображение параллелепипеда строится, исходя из того, что все его грани параллелограммы и, следовательно, изображаются параллелограммами (рис. 11). При изображении куба плоскость изображений обычно выбирается параллельной одной из его граней. В этом случае две грани куба, параллельные плоскости изображений (передняя и задняя), изображаются равными квадратами. Остальные грани куба изображаются параллелограммами (рис. 12). Аналогичным образом изображается прямоугольный параллелепипед (рис. 13).

Для того чтобы построить изображение призмы, достаточно построить многоугольник, изображающий ее основание. Затем, из вершин многоугольника провести прямые, параллельные некоторой фиксированной прямой, и отложить на них равные отрезки. Соединяя концы этих отрезков, получим многоугольник, являющийся изображением второго основания призмы (рис. 14). Для того чтобы построить изображение пирамиды, достаточно построить многоугольник, изображающий ее основание. Затем выбрать какую-нибудь точку, которая будет изображать вершину пирамиды, и соединить ее с вершинами многоугольника (рис. 15). Полученные отрезки будут изображать боковые ребра пирамиды.
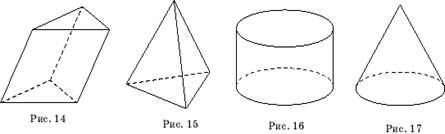
Для изображения цилиндра достаточно изобразить его основания в виде двух эллипсов, получающихся друг из друга параллельным переносом, и нарисовать две образующие, соединяющие соответствующие точки этих оснований (рис. 16). Для изображения конуса достаточно изобразить его основание в виде эллипса, отметить вершину и провести через нее две образующие, являющиеся касательными к этому эллипсу (рис. 17). Обратим внимание на тот факт, что плоское изображение, подчиняясь определенным законам, способно передать впечатление о трехмерном предмете. Однако при этом могут возникать иллюзии.
Порядок проведения работы (инструктаж):
1. Запишите в тетради тему занятия.
2. Внимательно прочитайте краткие теоретические сведения и выполните соответствующие записи в тетради.
3. Выполните изображение пространственных фигур на плоскости (рис. 11-17)
4. Ответьте на контрольные вопросы.
Записи в тетради должны содержать номер задания, формулировку задания и подробное решение.
Контрольные вопросы:
1. При каком положении отрезка относительно плоскостей проекции его проекция: а) равна самому отрезку; б) есть точка?
2. Отрезок проецируется параллельно на плоскость. Как проектируется середина отрезка на эту плоскость?
3. Может ли проекция отрезка быть больше отрезка, который проектируют?
4. Могут непараллельные прямые проектироваться в параллельные прямые? Приведите примеры.
5. Как расположены точки А и В относительно плоскости CDD1C1 (рис. 88)?
6. Плоскость фигуры не параллельна направлению проектирования. В какую фигуру проектируется: а) треугольник; б) параллелограмм?
