Элементы комбинаторики.
Правило суммы.
Пусть выбираются два объекта 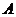 и
и 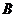 . Тогда, если объект
. Тогда, если объект 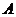 можно выбрать
можно выбрать 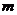 способами, а объект
способами, а объект 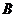 можно выбрать
можно выбрать  способами, то выбор "
способами, то выбор " 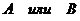 " можно осуществить
" можно осуществить  способами.
способами.
Правило произведения.
Пусть выбираются два объекта 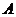 и
и 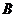 . Тогда, если объект
. Тогда, если объект 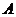 можно выбрать
можно выбрать 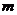 способами, а другой объект
способами, а другой объект 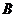 можно выбрать
можно выбрать  способами, то выбор пары "
способами, то выбор пары "  " в указанном порядке можно осуществить
" в указанном порядке можно осуществить 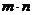 способами.
способами.
Размещением 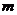 элементов из
элементов из  называется выборка расположенных в определенном порядке каких-либо
называется выборка расположенных в определенном порядке каких-либо 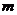 элементов из данных различных
элементов из данных различных  элементов, т.е. упорядоченное множество
элементов, т.е. упорядоченное множество 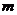 элементов из
элементов из  . Количество размещений обозначается
. Количество размещений обозначается 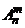 и вычисляется по формуле, содержащей
и вычисляется по формуле, содержащей 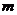 сомножителей:
сомножителей:
 .
.
Перестановкой из  различных элементов называется расположение этих элементов в строго фиксированном порядке, т.е. упорядоченное множество
различных элементов называется расположение этих элементов в строго фиксированном порядке, т.е. упорядоченное множество  различных элементов. Количество таких перестановок обозначается
различных элементов. Количество таких перестановок обозначается 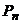 и находится по формуле
и находится по формуле
 ,
,
где 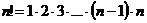 (по определению
(по определению  ).
).
Сочетанием 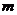 элементов из
элементов из  различных называется выборка каких-либо
различных называется выборка каких-либо 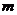 элементов из данных
элементов из данных  элементов без учета порядка, т.е. неупорядоченное множество
элементов без учета порядка, т.е. неупорядоченное множество 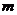 элементов из
элементов из  . Количество различных сочетаний обозначается
. Количество различных сочетаний обозначается 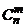 и вычисляется по формуле:
и вычисляется по формуле:
 или
или 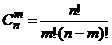
Случайные события.
Эксперимент, множество исходов которого состоит более чем из одного элемента, называют случайным или стохастическим. Множество всех возможных исходов эксперимента можно представить в виде:
 , где
, где 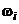 – элементарный исход эксперимента.
– элементарный исход эксперимента.
Для пространства элементарных исходов 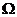 событием называется любое его подмножество. Говорят, что событие
событием называется любое его подмножество. Говорят, что событие 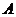 произошло, если в результате эксперимента имел место исход
произошло, если в результате эксперимента имел место исход 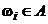 .
.
Суммой событий 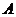 и
и 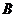 называется событие, состоящее в выполнении хотя бы одного из этих событий и обозначается
называется событие, состоящее в выполнении хотя бы одного из этих событий и обозначается  или
или 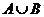 .
.
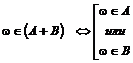
Произведением событий 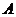 и
и 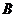 называется событие, состоящее в совместном выполнении этих событий и обозначается
называется событие, состоящее в совместном выполнении этих событий и обозначается  или
или 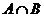 .
.
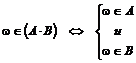
Противоположным по отношению к событию 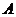 называется событие
называется событие 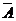 , состоящее в том, что событие
, состоящее в том, что событие 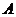 не произошло:
не произошло:
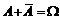 ,
,  ,
,
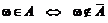 .
.
Разностью событий 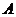 и
и 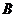 называется событие, состоящее в выполнении
называется событие, состоящее в выполнении 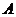 , но в невыполнении
, но в невыполнении 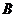 . Разность событий обозначается
. Разность событий обозначается  или
или  .
.

Система множеств (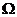 ,
, 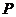 ) называется вероятностным пространством эксперимента с пространством элементарных исходов
) называется вероятностным пространством эксперимента с пространством элементарных исходов 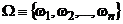 . Часто вероятностное пространство задают в виде таблицы.
. Часто вероятностное пространство задают в виде таблицы.
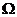
| 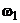
| 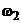
| … | 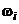
| 
| |
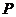
| 
| 
| … | 
| 
|
Вероятностью события 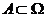 называется сумма вероятностей элементарных исходов, это событие образующих.
называется сумма вероятностей элементарных исходов, это событие образующих.
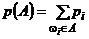
Классическая вероятность для вероятностного пространства с  равновозможными элементарными исходами
равновозможными элементарными исходами 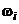 :
:
элементарные исходы 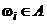 называют благоприятными для
называют благоприятными для 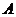 исходами, количество таких исходов обозначают
исходами, количество таких исходов обозначают 
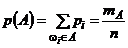 или
или 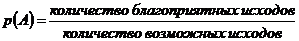 .
.
Теорема о вероятности суммы событий:
для двух событий 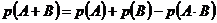
для трех событий

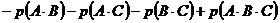 ,
,
для четырёх событий
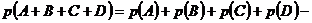
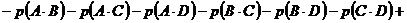

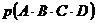 ,
,
и так далее.
Теорема о вероятности противоположного события: 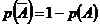 .
.
Если к комплексу условий, при которых была получена 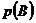 , добавить новое условие
, добавить новое условие 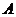 , то полученная вероятность события
, то полученная вероятность события 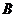 , найденная при условии, что
, найденная при условии, что 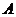 произошло, называется условной вероятностью события
произошло, называется условной вероятностью события 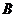 и обозначается
и обозначается 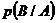 , или
, или  , или
, или  .
.
Теорема о вероятности произведения событий:
 .
.
Если 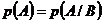 и, соответственно,
и, соответственно,  , то
, то 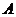 и
и 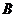 называются независимыми.
называются независимыми.
Для независимых событий 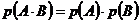 .
.
Группа событий 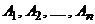 называется полной, если
называется полной, если 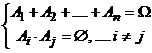 .
.
Формула полной вероятности.
Пусть 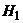 ,
, 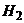 , …,
, …,  – полная группа событий, которую мы назовём гипотезами.
– полная группа событий, которую мы назовём гипотезами.
Известны вероятности  ,
,  , …,
, …, 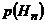 (обязательно
(обязательно 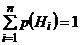 ) и условные вероятности события
) и условные вероятности события 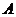 при реализации каждой из гипотез:
при реализации каждой из гипотез:  ,
, 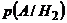 , …,
, …,  . Тогда
. Тогда

Формула Байеса.
При тех же условиях  ,
, 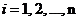 .
.
Случайные величины.
Под случайной величиной понимается переменная, которая в результате эксперимента в зависимости от случая принимает то или иное значение (одно из возможного множества своих значений, какое именно – заранее не известно).
Функцией распределения с.в. 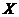 называется
называется  .
.
Свойства 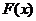 :
:
1) 
2)  ,
, 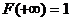
3) если 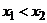 , то
, то 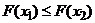
4) 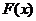 непрерывна слева, т.е.
непрерывна слева, т.е. 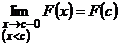
5)  (одна из основных формул!!!)
(одна из основных формул!!!)
6) 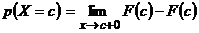 , т.е. если
, т.е. если 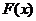 непрерывна в точке
непрерывна в точке 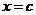 , то
, то 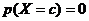 .
.
7) если 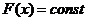 на
на  , то
, то 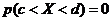 .
.
Случайная величина называется дискретной, если множество её значений конечно или счётно.
Рядом распределениядискретной случайной величины 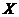 называется таблица, где в верхней строке перечислены в порядке возрастания все возможные значения с.в.
называется таблица, где в верхней строке перечислены в порядке возрастания все возможные значения с.в. 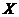 , а в нижней – вероятности для с.в.
, а в нижней – вероятности для с.в. 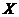 принять каждое из этих значений.
принять каждое из этих значений.
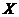
| 
| 
| ... | 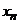
| ... |
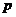
| 
| 
| ... | 
| ... |
Очевидно, что  .
.
Случайная величина называется непрерывной, если бесконечное несчётное множество её значений заполняют один или несколько интервалов (конечных или бесконечных) на числовой оси. Для непрерывной с.в. 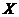 функция распределения непрерывна в любой точке и, следовательно,
функция распределения непрерывна в любой точке и, следовательно, 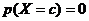 для
для  .
.
Плотностью распределения непрерывной случайной величины 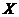 называется
называется  .
.
Свойства 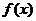 :
:
1)  (кривая плотности не может лежать ниже оси ОХ)
(кривая плотности не может лежать ниже оси ОХ)
2) 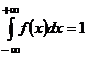 (площадь между осью
(площадь между осью  и графиком
и графиком 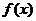 равна 1).
равна 1).
3) 
4) 
 (одна из основных формул!!!)
(одна из основных формул!!!)