Регрессионный анализ
Регрессионным анализом называется раздел математической статистики, объединяющий практические методы исследования корреляционной зависимости между случайными величинами по результатам наблюдений над ними. Сюда включаются методы выбора модели изучаемой зависимости и оценки ее параметров, методы проверки статистических гипотез о зависимости.
Пусть между случайными величинами Х и У существует линейная корреляционная зависимость (см. разд. 3.11). Это означает, что математическое ожидание У линейно зависит от значений случайной величины Х. График этой зависимости (линия регрессии У на Х) имеет уравнение М(У) = rХ + b, где r и b некоторые постоянные.
Линейная модель пригодна в качестве первого приближения и в случае нелинейной корреляции, если рассматривать небольшие инттервалы возможных значений случайных величин.
Пусть параметры линии регрессии r и b неизвестны, неизвестна и величина коэффициента корреляции rху. Над случайными величинами Х и У проделано n независимых наблюдений, в результате которых получены nпар значений: (Х1,У1), (Х2,У2), …, (Хn, Уn). Эти результаты могут служить источником информации о неизвестных значениях r, b, rху, надо только уметь эту информацию извлечь оттуда.
Неизвестная нам линия регрессии у = rх + b, как и всякая линия регрессии, имеет то отличительное свойство, что средний квадрат отклонений значений У от нее минимален. Поэтому в качестве оценок для r и b можно принять те их значения, при которых имеет минимум функция
F(r, b) = 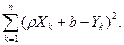
Такие значения r и b, согласно необходимым условиям экстремума, находятся из системы уравнений:
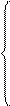
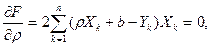
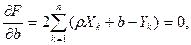
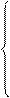 или
или
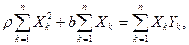
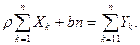
Решения этой системы уравнений дают оценки
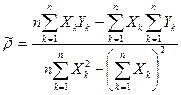 (4.20)
(4.20)
и
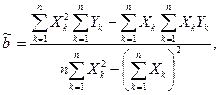 (4.21)
(4.21)
называемые оценками по методу наименьших квадратов.
Известно, что оценки по методу наименьших квадратов являются несмещенными и, более того, среди всех несмещенных оценок обладают наименьшей дисперсией.
Для оценки коэффициента корреляции можно воспользоваться тем, что rху = r 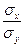 , где sх и sу средние квадратические отклонения случайных величин Х и У соответственно. Обозначим через sx и sу оценки этих средних квадратических отклонений на основе опытных данных. Оценки можно найти, например, по формуле (4.4). Тогда для коэффициента корреляции имеем оценку
, где sх и sу средние квадратические отклонения случайных величин Х и У соответственно. Обозначим через sx и sу оценки этих средних квадратических отклонений на основе опытных данных. Оценки можно найти, например, по формуле (4.4). Тогда для коэффициента корреляции имеем оценку
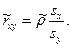 (4.22)
(4.22)
По методу наименьших квадратов можно находить оценки параметров линии регрессии и при нелиненой корреляции. Например, для линии регрессии вида М(У) = а Х2 + b X + c оценки параметров а, b и c находятся из условия минимума функции
F(a,b,c) = 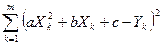 .
.
Пример 1. По данным измерений двух случайных величин
| Х | ||||||||||
| У |
найти коэффициент корреляции и уравнение линии регрессии У на Х.
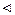 Вычислим величины, необходимые для использования формул 4.20 – 4.22:
Вычислим величины, необходимые для использования формул 4.20 – 4.22:
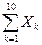 = 3 + 8 + 4 + 4 + … + 3 = 50;
= 3 + 8 + 4 + 4 + … + 3 = 50; 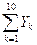 = 4 + 5 + 2 + 5 + … + 5 = 47;
= 4 + 5 + 2 + 5 + … + 5 = 47;
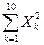 = 33 + 82 + 42 + 42 + … + 32 = 292;
= 33 + 82 + 42 + 42 + … + 32 = 292; 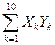 = 3×4 + 8×5 + 4×2 + … + 3×5 = 257.
= 3×4 + 8×5 + 4×2 + … + 3×5 = 257.
По формулам (4.20) и (4.21)
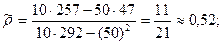
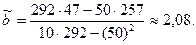
Итак, оценка линии регрессии имеет вид У = 0,52 Х + 2,08.
Так как 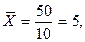 то по формуле (4.4)
то по формуле (4.4)
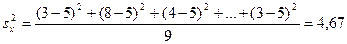 ;
; 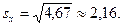
Аналогично, 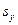 = 1,64. Поэтому в качестве оценки коэффициента корреляции имеем по формуле (4.22) величину
= 1,64. Поэтому в качестве оценки коэффициента корреляции имеем по формуле (4.22) величину 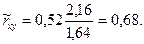
Если наблюдений много, то результаты их обычно группируют и представляют в виде корреляционной таблицы (табл. 4.1).
Таблица 4.1
 Х
Y Х
Y
| (х1,х2) | (х2,х3) | ... | (хk,xk+1) | n.y |
| (y1,y2) | n11 | n21 | ... | nk1 | n.1 |
| (y2,y3) | n12 | n22 | ... | nk2 | n.2 |
| ... | ... | ... | ... | ... | ... |
| (ym,ym+1) | n1m | n2m | ... | nkm | n.m |
| nx. | n1. | n2. | ... | nk. | n |
В этой таблице nij равно числу наблюдений, для которых Х находится в интервале (хi,xi+1), а У – в интервале (уj,yj+1). Через ni. обозначено число наблюдений, при которых ХÎ(хi,xi+1), а У произвольно. Число наблюдений, при которых УÎ(уj,yj+1), а Х произвольно, обозначено через n.j.
Если величины дискретны, то вместо интервалов указывают отдельные значения этих величин. Для непрерывных случайных величин представителем каждого интервала считают его середину и полагают, что 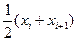 и
и  наблюдались nij раз.
наблюдались nij раз.
При больших значениях Х и У можно для упрощения вычислений перенести начало координат и изменить масштаб по каждой из осей, а после завершения вычислений вернуться к старому масштабу.
Пример 2. Проделано 80 наблюдений случайных величин Х и У. Результаты наблюдений представлены в виде табл. 4.2.
Таблица 4.2
 Х
У Х
У
| -2 0,5 - 1,5 | -1 1,5 – 2,5 | 2,5 – 3,5 | 3,5 – 4,5 | 4,5 – 5,5 | n.y |
 -1 14 –16
0 16 - 18
1 18 - 20
2 20 - 22 -1 14 –16
0 16 - 18
1 18 - 20
2 20 - 22
| - | - - | - | - | - | |
| nx. |
Найти линию регрессии У на Х. Оценить коэффициент корреляции.
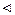 Представителем каждого интервала будем считать его середину. Перенесем начало координат и изменим масштаб по каждой оси так, чтобы значения Х и У были удобны для вычислений. Для этого перейдем к новым переменным
Представителем каждого интервала будем считать его середину. Перенесем начало координат и изменим масштаб по каждой оси так, чтобы значения Х и У были удобны для вычислений. Для этого перейдем к новым переменным 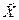 = Х - 3 и
= Х - 3 и 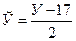 . Значения этих новых переменных указаны соответственно в самой верхней строке и самом левом столбце табл. 4.2.
. Значения этих новых переменных указаны соответственно в самой верхней строке и самом левом столбце табл. 4.2.
Чтобы иметь представление о виде линии регрессии, вычислим средние значения 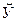 при фиксированных значениях
при фиксированных значениях 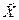 :
:
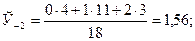
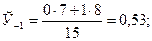
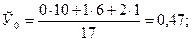
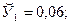
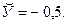
Нанесем эти значения на координатную плоскость, соединив для наглядности их отрезками прямой (рис. 4.5).

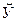


 1
1
 |
-2 -1 0 1 2 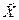
Рис. 4.5
По виду полученной ломанной линии можно предположить, что линия регрессии У на Х является прямой. Оценим ее параметры. Для этого сначала вычислим, с учетом группировки данных в таблице, все величины, необходимые для использования формул (4.20) – (4.22):
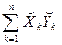 =
= 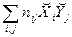 = 1× (-1)×5 + 2× (-1) ×7 + … +2× (-2) ×3 = -53;
= 1× (-1)×5 + 2× (-1) ×7 + … +2× (-2) ×3 = -53;
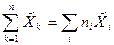 = (-2) × 18 + (-1) × 15 + 0 × 17 + 1× 18 + 2 × 12 = - 9:
= (-2) × 18 + (-1) × 15 + 0 × 17 + 1× 18 + 2 × 12 = - 9:
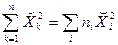 = 4×18 + 1×15 + 1×18 + 4×12 = 153;
= 4×18 + 1×15 + 1×18 + 4×12 = 153;
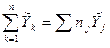 = (-1) × 12 + 0 × 32 + 1× 32 + 2 × 4 = 28.
= (-1) × 12 + 0 × 32 + 1× 32 + 2 × 4 = 28.
Тогда
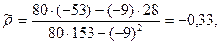
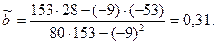
В новом масштабе оценка линии регрессии имеет вид 
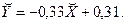
График этой прямой линии изображен на рис. 4.5.
Для оценки 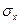 по корреляционной таблице можно воспользоваться формулой (4.4):
по корреляционной таблице можно воспользоваться формулой (4.4):
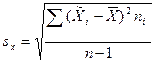 = 1,38.
= 1,38.
Подобным же образом можно оценить 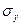 величиной sy = 0,75. Тогда оценкой коэффициента корреляции может служить величина
величиной sy = 0,75. Тогда оценкой коэффициента корреляции может служить величина 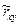 = - 0,33
= - 0,33 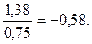
Вернемся к старому масштабу:
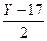 = - 0,33(Х-3) +0,31, или У = - 0,66 Х + 19,6.
= - 0,33(Х-3) +0,31, или У = - 0,66 Х + 19,6.
Коэффициент корреляции пересчитывать не нужно, так как это величина безразмерная и от масштаба не зависит. 
Пусть некоторые физические величины Х и У связаны неизвестной нам функциональной зависимостью у = f(х). Для изучения этой зависимости производят измерения У при разных значениях Х. Измерениям сопутствуют ошибки и поэтому результат каждого измерения случаен. Если систематической ошибки при измерениях нет, то у = f(х) играет роль линии регрессии и все свойства линии регрессии приложимы к у = f(х). В частности, у = f(х) обычно находят по методу наименьших квадратов.
Пример 3. Получена выборка значений величин Х и У:
| Х | ||||||||
| У |
Для представления зависимости между величинами предполагается использовать модель У = 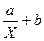 . Найти оценки параметров а и b.
. Найти оценки параметров а и b.
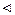 Рассмотрим сначала задачу оценки параметров этой модели в общем виде.Линия У =
Рассмотрим сначала задачу оценки параметров этой модели в общем виде.Линия У = 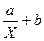 играет роль линии регрессии и поэтому параметры ее можно найти из условия минимума функции (сумма квадратов отклонений значений У от линии должна быть минимальной по свойству линии регрессии)
играет роль линии регрессии и поэтому параметры ее можно найти из условия минимума функции (сумма квадратов отклонений значений У от линии должна быть минимальной по свойству линии регрессии)
F(a,b) = 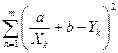 .
.
Необходимые условия экстремума приводят к системе из двух уравнений:
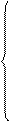
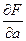 = 2
= 2 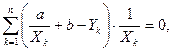
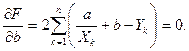
Откуда
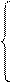 а
а 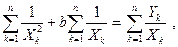 (4.23)
(4.23)
а 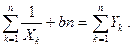 (4.24)
(4.24)
Решения системы уравнений (4.23) и (4.24) и будут оценками по методу наименьших квадратов для параметров а и b.
На основе опытных данных вычисляем:
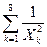 =
= 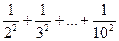 = 0,56;
= 0,56; 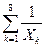 =
= 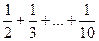 = 1,87;
= 1,87;
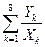 =
= 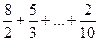 = 8,82;
= 8,82; 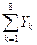 = 8 + 5 + 2 + …+ 2 = 29.
= 8 + 5 + 2 + …+ 2 = 29.
В итоге получаем систему уравнений (4.23) и (4.24) в виде
0,56 а + 1,87 b = 8,82 и 1,87 a + 8 b = 29.
Эта система имеет решения 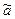 = 16,7 и
= 16,7 и 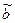 = - 0,25.
= - 0,25. 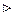
Практическое занятие 4 июня 2020г..
1. По данным измерений двух случайных величин
| Х | ||||||||||
| У |
найдите коэффициент корреляции и уравнение линии регрессии У на Х.
Ответ: 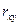 0,743; У = 0,8 + 0,25.
0,743; У = 0,8 + 0,25.
2. Проделано 100 наблюдений случайных величин Х и У. Результаты наблюдений представлены в виде табл. 4.3.
Таблица 4.3
| Х У | 40 – 50 | 50 – 60 | 60 – 70 | 70 – 80 |
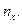
|
| 10 – 12 | |||||
| 12 – 14 | |||||
| 14 – 16 | |||||
| 16 – 18 | |||||
| n.y |
Вычислите коэффициент корреляции и найдите уравнение прямой регрессии У на Х.
Ответ: 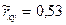 ; У = 0,11 Х + 12.
; У = 0,11 Х + 12.
3. Корреляционная зависимость между случайными величинами Х и У имеет вид у = а + b / x. Найдите оценки параметров а и b по результатам измерений:
| х | ||||
| у | 5,25 | 3,5 | 3,25 |
Ответ: а = 2, b = 12.
4.Считая, что корреляционная зависимость между величинами Х и У имеет вид у = a х2 + bх + g, найдите оценки параметров a, b, g по выборке наблюдений значений Х и У:
| х | -2 | -1 | |||
| у | 4,8 | 0,4 | -3,4 | 0,8 | 3,2 |
Ответ: a = 1,54; b = - 0,28; g = - 1,93.