Рассмотрим температурную зависимость концентрации электронов в п/п “n”типа.(рис.3.5)
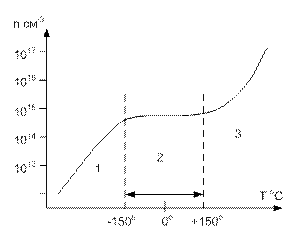
Рис.3.5 Температурная зависимость концентрации носителей п/п
Три области:
1- средняя энергия фононов мала в сравнении с энергией ионизации,- лишь часть доноров ионизирована (область примесной проводимости).
2- средняя энергия фононов соизмерима с энергией ионизации примесей, но меньше ширины запрещенной зоны- все доноры ионизированы, а концентрация собственных электронов мала (область примесного истощения).
Число свободных электронов- const,и их концентрация равна концентрации доноров, те в 1,2 преобладают примесные основные носители.
3 - средняя энергия фононов увеличивается настолько что концентрация собственных носителей становиться больше концентрации доноров (область собственной проводимости).
П/п приборы могут нормально функционировать только в температурном диапазоне 2, когда концентрация основных носителей практически не зависит от температуры и равна концентрации примесей.
Поэтому область 2 определяет максимальную и минимальную рабочие температуры приборов.
Процессы переноса заряда в полупроводниках
Процесс переноса зарядов может наблюдаться в полупроводниках при наличии электронов в зоне проводимости
Перенос носителей зарядов может происходить либо под действием электрического поля (Дрейф), либо из-за неравномерности концентрации носителей заряда (Диффузия),
Дрейф носителей заряда
Дрейф - направленное движение носителей заряда под действием электрического поля.
Электроны получая ускорение в эл. поле, приобретают на длине свободного пробега 10-8 – 10-4 эВ. и переходят на более высокие э.у. При очередном соударении электрон отдает энергию решетке (фонону) и возвращается на один из низко лежащих энергетических уровня. Так можно представить процесс электропроводности.
*) длиной свободного пробега носителей заряда, определяется как среднее расстояние, проходимое носителем между двумя последовательными актами рассеяния.
Длина свободного пробега (lср), среднее время свободного пробега (tср) и средняя скорость теплового хаотического движения (Vтср), связаны соотношением
lср = Vтср tср (3.10)
[Vтср ~ 105 м/сек]
Скорость дрейфа
Vдр,ср = (q/m) E = mE (3.11)
q – заряд электрона;
m – масса электрона;
E – напряженность электрического поля
Коэффицент пропорциональности m называется подвижностью электронов,
т. е. подвижность - величина, численно равная средней скорости их направленного движения в электрическом поле с напряженностью, равной 1В/м.
| п/п | Ge | Si | GaAs | SiC |
| mn [м2/в.с] | 0.39 | 0.13 | 0.02-0.1 | |
| mp [м2/в.с] | 0.19 | 0.05 | 0.04 | 5.10-4 |
Во всех практически используемых п/п при Т=300К подвижность падает с ростом поля, в сильных полях m ~1/E, т.е Vдрейф~ const~5.104 м/сек (Е~5кВ/см)
пример: U=1B; l=100нм (100 10-9м); тогда E= 10 кВ/см) [E=U/l]

Рис.3.6 Зависимость дрейфовой скорости от напряженности электрического поля
В результате дрейфа электронов в полупроводнике появляется электронная составляющая плотности дрейфового тока (А/м2), которую запишем на основании закона Ома:
Jn др = qnmnE (3.12)
q - заряд электрона. n –концентрация электронов в п/п.
Аналогично, дырочная составляющая плотности дрейфового тока
JP др = qpmPE (3.13)
Полная плотность дрейфового тока при наличии свободных электронов и дырок равна сумме электронной и дырочной составляющих:
J др = qnmnE + qpmPE (3.14)
n, p – концентрации свободных носителей.
Закон Ома в дифференциальной форме:
плотность тока ~ напряженность эл. поля *удельную проводимость (s-коэффициент)
J = s E = (1/r) E (3.15)
Сравнивая (3.15) и (3.12, 3.13), тогда удельная проводимость
s = mnqn + mpqp (3.16)
Ток c плотностью J через площадку S равен
I = JS (3.17)