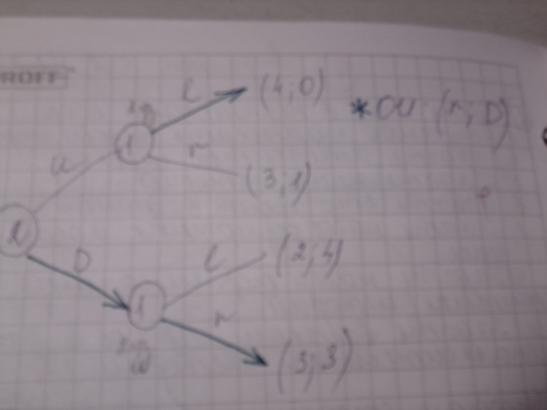
Что нужно, чтобы задать игру в позиционной форме?
-игроки
-набор историй (какими путями можно попасть в узел)- это последовательность ходов для каждого узла
-кто ходит в данном узле
-набор возможных ходов в узле
-набор термин-х историй
-выигрыш игроков в каждой Т.И.
Игра с совершенной информацией – это игра, в которой кажд.игрок,находясь в конкр.узле,знает,где он и как туда попал.
Чистая стратегия в игре с соверш.инф. – это полный набор действий игрока в кажд.узле
ПР: кучки, Английя и нормандия, Деньги в шляпе
3. Доминирование — ситуация, при которой одна из стратегий некоторого игрока дает больший выигрыш, нежели другая, при любых действиях его оппонентов.
- Стратегия В доминирует стратегию A, если при любом поведении остальных игроков использование стратегии В приводит к не худшему исходу, нежели использование А. Различают строгое доминирование, когда В дает больший выигрыш, чем А, в любых условиях, и слабое доминирование, если при некоторых действиях других игроков В обеспечивает больший выигрыш, чем А, а при других — одинаковый с ней.
- Стратегия В доминируется стратегией A, если при любом поведении остальных игроков стратегия В приводит к не лучшему исходу, нежели стратегия А. Аналогично предыдущему случаю, стратегия может доминироваться строго и слабо.
- Стратегия B называется строго доминирующей, если она строго доминирует любую другую допустимую стратегию игрока.
- Стратегия B называется слабо доминирующей, если она доминирует любую другую допустимую стратегию игрока, при этом некоторые из них доминируются слабо.
- Стратегия B называется строго доминируемой, если существует другая стратегия, которая строго ее доминирует.
- Стратегия B называется слабо доминируемой, если существует другая стратегия, которая слабо ее доминирует.
4)Лучший ответ(BR) - это стратегия, обеспечивающая максимум выигрыша i -го игрока в ответ на какое-либо действие соперника. 


Мы помимо доминируемых, можем также считать нерациональными те стратегии, которые не являются лучшими ответами ни на какие действия соперника. И последовательно удаляя такие стратегии, мы можем сойтись до множества рационализируемых исходов. Очень хорошо, если это множество состоит из 1 исхода, тогда мы считаем, что это решение.
Пример: Игра «Партнерство» или игра «Пенальти»
Игра «Пенальти»
| l | r | |
  L L
| 4; -4 | 9;-9 |
| M | 6; -6 | 6; -6 |
| R | 9;-9 | 4; -4 |
Мы видим, что нет решения. Но мы можем удалять стратегии, не обеспечивающие максимальный выигрыш, ни при каком мнении о действии игрока.
В нашем случае данной стратегией будет стратегия М, потому что она не является лучшим ответом первого игрока ни на какие действия второго игрока.
5) Равновесие Нэша - это пересечение множеств лучших ответов.
Свойство РН:

Ни у одного из игроков нет строгого желания в одиночку покинуть равновесие Нэша.
Пример:
| a | b | c | |
| A | 1;1 | 0;0 | 2;2 |
| B | 0;2 | 4;1 | 3;3 |
| C | 3;4 | 3;2 | 1;0 |
РНЧС: (С,а) и (B,c)
Чтобы построить график приведем исходную матрицу к матрице 2х2 с помощью удаления доминируемых стратегий. Стратегия а строгодоминирует стратегию b. Получаем:
| a | c | |
| A | 1;1 | 2;2 |
| B | 0;2 | 3;3 |
| C | 3;4 | 1;0 |
Далее мы может удалить стратегию А, потому что она не является лучшим ответом ни на какую стратегию соперника. Получаем:
| a | c | |
| B | 0;2 | 3;3 |
| C | 3;4 | 1;0 |
M(u1[B,q])=3-3q
M(u1[C,q])=2q+1 отсюда следует q=2/5
M(u2[a,p])=4-2p
M(u2[c,p])= 3p отсюда следует p=4/5
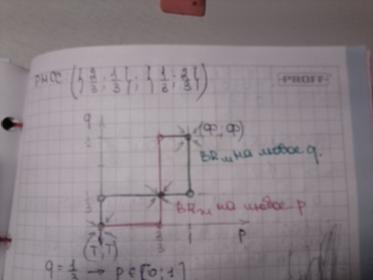
График:

6. Равновесие Нэша в смешанных стратегиях. Определение. Предпосылки для использования. Привести пример игры, найти в ней множество всех равновесий в чистых и смешанных стратегиях. Проиллюстрировать решение на графике лучших ответов.
Равновесие Нэша в смешанных стратегиях – такой исход (р1*…рn*), где pi*=BR; (p-i*) Ұi =1n (для любого p-i игрока).
Предпосылки для использования – если РНЧС нет или оно не единственно, то может существовать равновесие в смешанных стратегиях. Смешанная стратегия войдет в равновесие, если другой игрок, в ответ на эту смешанную стратегию, будет получать одинаковый выигрыш от любых собственных действий. Соответственно, у игроков не будет необходимости думать о том, какие стратегии играть в ответ на смешанное равновесие.
Игра «Семейный спор»

7. Позиционные игры с совершенной информацией. Определение совершенной информации. Определение чистой стратегии в игре с СИ. Метод обратной индукции. Привести пример позиционной игры с СИ. Найти решение методом обратной индукции.
Игра в позиционной форме называется игрой с совершенной информацией, если каждое информационное множество состоит из единственной вершины. В противном случае игра называется игрой с несовершенной информацией.
Совершенная информация – ситуация в игре, когда все информационные множества состоят не более чем из одного узла.
Чистая стратегия в игре с СИ – это полный набор действий игрока в каждом узле.
Метод обратной индукции - это метод поиска решения в позиционных играх с совершенной информацией. Для того, чтобы найти решение, надо посмотреть на самые последние узлы, выяснить как там будет вести себя игрок, принимающий решение. Обратиться к предыдущим узлам, принять решение исходя из знания о поведении соперника в следующих узлах.