В процессе роста дерева, под влиянием происходящих в нем различных физиологических процессов: фотосинтеза, дыхания, водообмена и обмена питательных веществ, происходит увеличение размеров в высоту (из точки роста, находящейся в верхушечной почке последнего годичного побега) и толщину (вследствие деления клеток камбиального слоя). В результате этого увеличиваются площадь сечения и объем дерева. Это увеличение и называется приростом.
Различают средний (Δ) и текущий (Z) приросты дерева. Средний прирост характеризует величину изменения таксационного показателя в среднем в единицу времени в течение всей жизни дерева Δ=Т/А.
Текущий прирост есть величина, на которую изменяется таксационный показатель за определенный период (n лет) жизни дерева. Он определяется как разность в величине таксационного показателя в возрасте А и А — n лет. В зависимости от длины периода n лет различают:

Вследствие малой (трудноизмеримой) величины годичного прироста и его большой изменчивости по годам последний вид прироста на практике определяют наиболее часто, принимая за n период в 3, 5 или 10 лет.
У срубленного дерева величина текущего прироста по высоте и диаметру может быть определена непосредственным измерением, а по площади сечения и объему — путем расчетов. Известно множество способов определения объемного прироста. Наиболее полная их сводка дана в монографии В. В. Антанайтиса и В. В. Загреева «Прирост леса [18].
В отечественной практике наиболее часто для определения объемов срубленных на пробных площадях модельных (учетных) деревьев используют простую или сложную формулы срединных сечений (формулы Губера):

V = (g1+ g2+ g3+…+g n)*L+Vверш
где V — объем ствола; g1/2 — площадь сечения ствола на середине его длины; L — длина ствола; g1 g2, g3, gn — срединные площади сечений отдельных и равных по длине отрезков ствола; / — длина отрезков; VBep — объем вершинки ствола.
Тогда среднепериодическйй прирост по объему ствола за n лет будет равен:

Задача. Определить прирост по объему срубленного ствола длиной 23 м по простой формуле срединного сечения.
Решение. Путем постепенного отрубания вершины ствола и подсчета числа годичных колец на месте отруба находим прирост в высоту, например, за последние 10 лет. Допустим, что он оказался равным 1,0 м. Путем измерения определяем диаметры на половине длины ствола в возрасте А лет (11,5 м) в коре — 13,0 см, без коры — 12,4 см и в возрасте А — n лет (11,0 м) в коре — 13,3 см, без коры — 12,7 см. С помощью приростного бурава или на зарубе, сделанном на половине длины ствола в возрасте А — n лет (11,0 м), определяем прирост по радиусу за последние 10 лет — 0,75 см. Вычитая удвоенную величину радиального прироста (прирост по диаметру) из диаметра без коры, получаем диаметр на половине длины ствола в возрасте А — n лет (без коры dА-n= 12,7—1,5= 11,2 см). По таблице находим площади поперечных сечений, соответствующие срединным диаметрам без коры в возрасте А лет — 0,01208 ма и А — n лет — 0,00985 м2.
Подставляя полученные данные в приведенную выше формулу, определяем среднепериодический прирост по объему:

Точность определения объемного прироста этим способом невысока и колеблется в пределах ±12—20 %. Она значительно повышается (до ±3— 5 %), если объемы стволов в возрасте А и А — n лет определяют по сложной формуле срединных сечений.
С меньшими трудозатратами, но и некоторой потерей точности Zv срубленного дерева можно определить одним из следующих упрощенных способов:
1. По площади боковой поверхности ствола (по А. В. Тюрину):
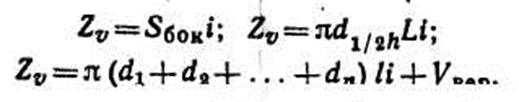
где Sбок — площадь боковой поверхности ствола; d1/2h— диаметр на середине длины ствола; d1 d2 — диаметры на середине отдельных отрезков; i — ширина годичного слоя (радиальный прирост).
2. По формуле М. Л. Дворецкого
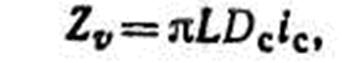
где Dc — средний из срединных диаметров двухметровых отрезков; i с –средняя ширина годичного слоя на высотах 1,3 м, 1/2h и l/4h
3. По формуле Б. А. Шустова

где D1, d1— диаметры на высоте 1,3 м без коры в возрасте А и А — n лет; D2, d2 — диаметры на половине длины ствола без коры в возрасте А и А — n лет; Н, h — длина ствола в возрасте А и А — n лет.
Для сравнительной оценки текущего прироста отдельных деревьев чаще используют не абсолютные значения прироста, а их проценты (Р).
Процент среднепериодического текущего прироста по объему (Pv) срубленного дерева есть сумма процентов прироста по площади сечения, высоте и видовому числу:

Приближенные значения процентов прироста дают формулы

С целью некоторого их уточнения Г. М. Турский предложил формулу
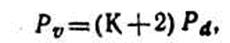
где значение К меняется в зависимости от энергии роста в высоту в пределах от 0 до 1,3: для деревьев, прекративших рост в высоту, К=0, имеющих слабый рост — 0,4, умеренный — 0,7, хороший — 1,0 и очень хороший — 1,3.
На практике наиболее часто процент прироста по объему определяют по формуле Пресслера

У растущих деревьев прирост по высоте Zh не может быть установлен прямым измерением, а величину радиального прироста Zr можно измерить лишь на высоте, близкой к высоте 1,3 м. Поэтому прирост по объему определяют путем внесения в расчетные формулы поправочных коэффициентов, учитывающих энергию роста в высоту и характер изменения ширины годичного слоя по длине ствола, либо путем установления прямых связей объемного прироста с приростом по диаметру или площади сечения.
Чаще всего объемный прирост растущих деревьев определяется через процент прироста одним из следующих способов:
1. По приведенным выше формулам связи Pv с Рd.
2. По формуле Шнейдера
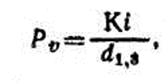
где К — коэффициент, определяемый по приведенной ниже таблице в зависимости от длины кроны и энергии роста в высоту; i — средняя за n лет ширина годичного слоя; d1,3 — диаметр на высоте груди без коры в возрасте А — n лет.
Коэффициент К
| Начало кроны | Рост в высоту | |||||
| прекратился | слабый | умеренный | хороший | очень хороший | превосходный | |
| Ниже1/2h | ||||||
| Между 1/2h и 3/4h | ||||||
| Выше 3/4h |
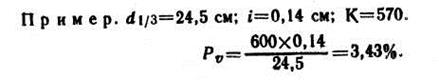
3. По формуле М. Преслера

где r — относительный диаметр, определяемый по формуле r•=d1,3/Zd — показатель степени, характеризующий рост дерева в высоту и изменяющийся в пределах от 2 до 3,5.
Расчеты упрощаются при пользовании таблицей 141.
141. Прирост по объему стволов, %, растущих деревьев
| Относи-тельный диаметр | Прирост за n лет при росте в высоту по группам | Относи-тельный диаметр | Прирост за n лет при росте в высоту по группам | ||||||
| II | III | IV | V | II | III | IV | V | ||
| 7,9 | 9,0 | ||||||||
| 7,4 | 8,5 | 9,5 | |||||||
| 7,0 | 7,9 | 8,9 | |||||||
| 6,5 | 7,5 | 8,4 | 9,5 | ||||||
| 6,2 | 7,1 | 8,0 | 8,9 | ||||||
| 5,9 | 6,8 | 7,6 | 8,5 | ||||||
| 5,6 | 6,4 | 7,2 | 8,0 | ||||||
| 5,4 | 6,1 | 6,9 | 7,8 | ||||||
| 5,1 | 5,9 | 6,6 | 7,4 | ||||||
| 4,9 | 5,6 | 6,3 | 7,0 | ||||||
| 4,7 | 5,4 | 6,1 | 6,8 | ||||||
| 4,6 | 5,2 | 5,9 | 6,5 | ||||||
| 4,4 | 5,1 | 5,7 | 6,3 | ||||||
| 4,3 | 4,9 | 5,5 | 6,1 | ||||||
| 4,2 | 4,7 | 5,3 | 5,9 | ||||||
| 4,0 | 4,5 | 5,1 | 5,7 | ||||||
| 3,7 | 4,2 | 4,7 | 5,3 | ||||||
| 3,5 | 3,9 | 4,4 | 4,9 | ||||||
| 3,3 | 3,7 | 4,2 | 4,6 | ||||||
| 3,2 | 3,6 | 4,0 | 4,4 | ||||||
| 2,9 | 3,4 | 3,8 | 4,1 | ||||||
| 9,1 | 2,6 | 3,0 | 3,4 | 3,8 | |||||
| 8,5 | 9,7 | 2,3 | 2,7 | 3,0 | 3,4 |
Выбор группы роста производится в зависимости от высоты, с которой начинается крона дерева, и энергии роста в высоту по следующей вспомогательной таблице
| Начало кроны | Рост в высоту | ||
| слабый | умеренный | хороший | |
| Ниже1/2h | II | III | IV |
| Между 1/2h и 3/4h | II,5 | III,5 | IV,5 |
| Выше 3/4h | III | IV | V |
Пример. Определить среднепериодический (за 10 лет) прирост по объему растущего дерева в %, если D1,3=24,5 cm, Zd=2,7 см, r=24,5/2,7= =9,0, крона расположена выше 3/4 h, рост в высоту — умеренный.
По вспомогательной таблице находим, что это IV группа роста. Тогда по таблице 141 Рv=35% за 10 лет и Рv = 3,5% в год.