Цели и задачи урока: ввести понятия синуса, косинуса и тангенса острого угла прямоугольного треугольника, формировать знание основного тригонометрического тождества.
- закрепить полученные знанияпри решении прямоугольных треугольников, используя синус, косинус, тангенс острого угла.
Задания.
1. Рассмотрите теоретический материал. В тетради постройте прямоугольный треугольник АВС, в котором угол С – прямой. Запишите из предложенного конспекта то, что выделено желтым.
| Синус, косинус, тангенс острого угла прямоугольного треугольника. Основное тригонометрическое тождество. |
Рассмотрим прямоугольный треугольник АВС
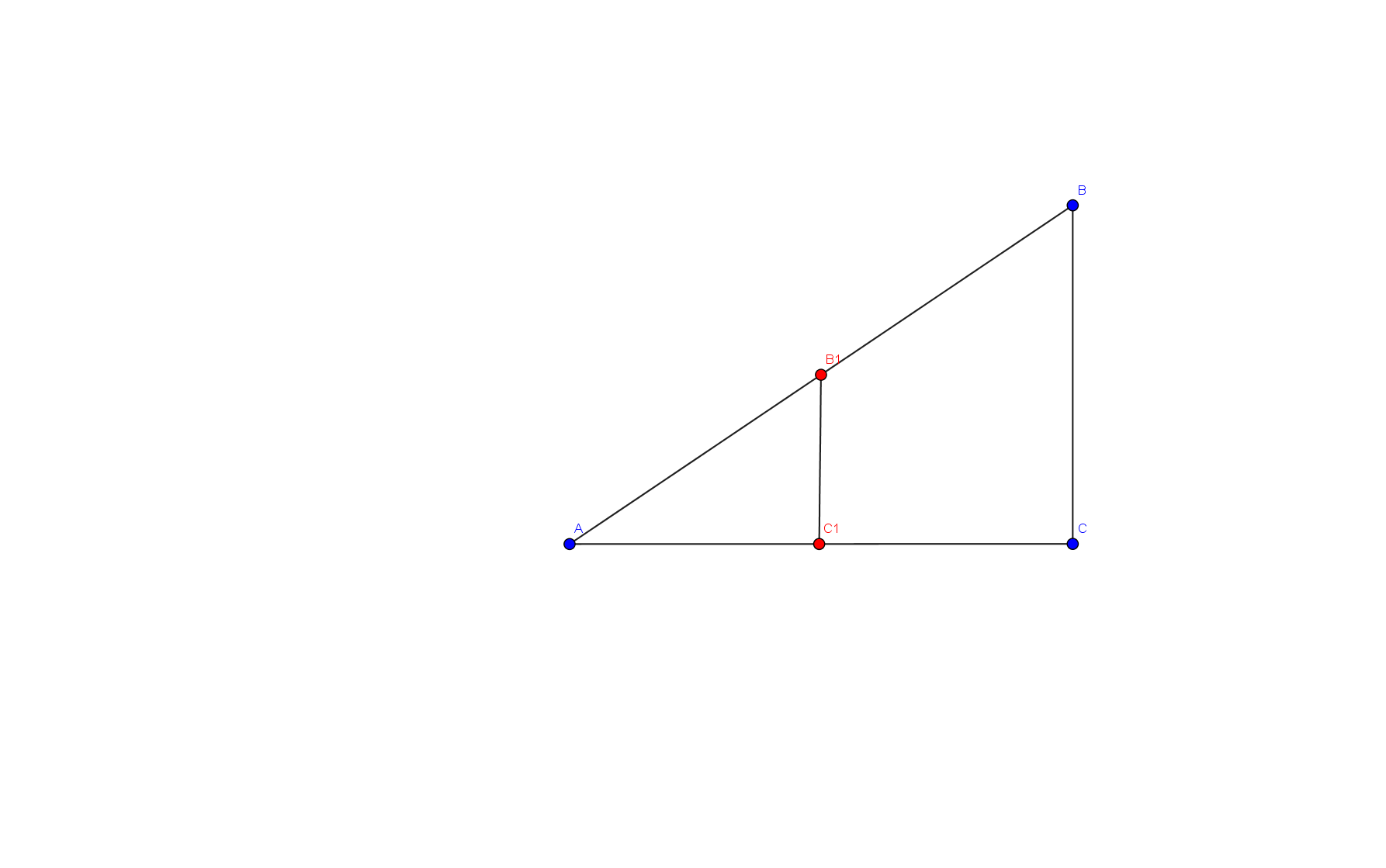
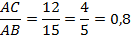 Возьмем точку С 1 на отрезке АС, проведем к нему перпендикуляр С 1 В 1
Возьмем точку С 1 на отрезке АС, проведем к нему перпендикуляр С 1 В 1
 Измерим отрезки АС 1 и АВ 1. AC 1=6; AB 1=7,5.
Измерим отрезки АС 1 и АВ 1. AC 1=6; AB 1=7,5.
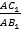 = = 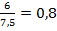 Возьмем точку С 2 на продолжении отрезка АС и проведем перпендикуляр С 2 В 2.
Возьмем точку С 2 на продолжении отрезка АС и проведем перпендикуляр С 2 В 2.
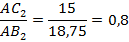 Заметим, что катет АС является прилежащим к углу А треугольника АВС. Катет АС 1 является прилежащим к углу А в треугольнике АС 1 В 1. Катет АС 2 также является прилежащим к углу А, но уже в треугольнике АС 2 В 2. Получилось, что отношение прилежащего катета к гипотенузе во всех трех случаях равно 0,8. Очевидно, что это отношение зависит только от угла А.
Заметим, что катет АС является прилежащим к углу А треугольника АВС. Катет АС 1 является прилежащим к углу А в треугольнике АС 1 В 1. Катет АС 2 также является прилежащим к углу А, но уже в треугольнике АС 2 В 2. Получилось, что отношение прилежащего катета к гипотенузе во всех трех случаях равно 0,8. Очевидно, что это отношение зависит только от угла А.
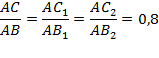 Определение: Отношение прилежащего катета к гипотенузе называется косинусом острого угла прямоугольного треугольника
Определение: Отношение прилежащего катета к гипотенузе называется косинусом острого угла прямоугольного треугольника
 Отношение противолежащего катета к гипотенузе называется синусом острого угла прямоугольного треугольника
sinA=
Отношение противолежащего катета к гипотенузе называется синусом острого угла прямоугольного треугольника
sinA=  Отношение противолежащего катета к прилежащему называется тангенсом острого угла прямоугольного треугольника
tgA=
Отношение противолежащего катета к прилежащему называется тангенсом острого угла прямоугольного треугольника
tgA=  Синус, косинус и тангенс острого угла прямоугольного треугольника – это числа. Подумайте, какими числами могут быть синус, косинус и тангенс.
tgA =
Синус, косинус и тангенс острого угла прямоугольного треугольника – это числа. Подумайте, какими числами могут быть синус, косинус и тангенс.
tgA =  Докажем утверждение:
Если острый угол одного прямоугольного треугольника равен острому углу другого прямоугольного треугольника, то синусы этих углов равны, а также косинусы этих углов равны и тангенсы этих углов равны.
Докажем утверждение:
Если острый угол одного прямоугольного треугольника равен острому углу другого прямоугольного треугольника, то синусы этих углов равны, а также косинусы этих углов равны и тангенсы этих углов равны.
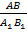 = = 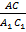 = = 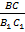 ,следовательно ,следовательно 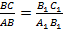 , поэтому sinA = sinA 1
Из равенства отношений , поэтому sinA = sinA 1
Из равенства отношений
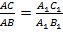 , следовательно cosA = cosA 1
Из равенства отношений , следовательно cosA = cosA 1
Из равенства отношений
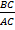 = = 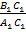 , следовательно tgA = tgA 1
В прямоугольном треугольнике выполняется теорема Пифагора - , следовательно tgA = tgA 1
В прямоугольном треугольнике выполняется теорема Пифагора - 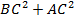 = = 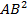 .
Разделим почленно обе части равенства на АВ 2 .
Разделим почленно обе части равенства на АВ 2
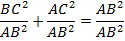 Используя определение синуса и косинуса угла А, получим
Используя определение синуса и косинуса угла А, получим
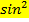 A+ A+ 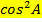 = 1
ОСНОВНОЕ ТРИГОНОМЕТРИЧЕСКОЕ ТОЖДЕСТВО
Из основного тригонометрического тождества зная косинус угла, легко найти его синус и наоборот
Пример: cosA =0,8
Найдите sinA
Решение:
По основному тригонометрическому тождеству получим = 1
ОСНОВНОЕ ТРИГОНОМЕТРИЧЕСКОЕ ТОЖДЕСТВО
Из основного тригонометрического тождества зная косинус угла, легко найти его синус и наоборот
Пример: cosA =0,8
Найдите sinA
Решение:
По основному тригонометрическому тождеству получим
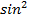 A+ A+ 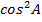 = 1, = 1,
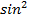 A+ A+ 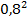 = 1, = 1,
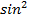 A = 1−0,82 A = 1−0,82
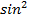 А = 0,36
sinA = 0,6 А = 0,36
sinA = 0,6
|
2.Посмотрите видеофрагмент урока по ссылке https://www.youtube.com/watch?v=BirCrL_XKQ0
3). Разобрать решение задачи (прикреплено) 



4. Домашнее задание. Выучить формулы, тождества из п. 68, решитьзадачи №№591(а), 592 (д), решить задачу №1 (В треугольнике АВС с прямым углом С найти синус, косинус, тангенс угла В, если ВС = 6 см, АВ = 10см.
В тетради записываем число:
Двадцать восьмое марта