Центробежные компрессоры.

КОМПРЕССОРЫ

Компрессоры предназначены для сжатия и перемещения раз- } личных газов. Они подразделяются на поршневые, ротационные, центробежные и осевые.

П 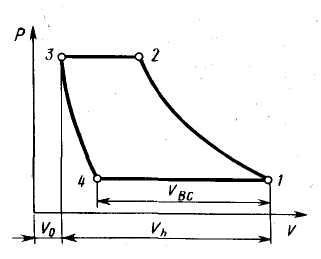оршневые компрессоры. Теоретический рабочий процесс одноступенчатого поршневого компрессора изображается в виде индикаторной диаграммы, построенной в координатах р, V (рис. 6.1).

Отношение объема всасывания V_вс к рабочему объему цилиндра V_h называют объемным кпд ступени компрессора:

, (6.1)

где σ = V ₀/ V_h — относительный объем вредного пространства; V ₀и V_h — соответственно вредный и рабочий объемы цилиндра;

λ — степень повышения давления;

т — показатель политропы расширения газа, остающегося во вредном объеме.

Под степенью повышения давления понимают отношение давления на выходе из ступени к давлению на входе в ступень:

λ= р ₂/ р ₁. (6.2)

Д ействительный рабочий процесс одноступенчатого поршневого компрессора изображен индикаторной диаграммой (рис. 6.2) и отличается от теоретического главным образом наличием потерь давления во впускном и нагнетательном клапанах.

Отношение действительной подачи компрессора V к теоретической подаче V_т называют коэффициентом подачи компрессора:

η_V=V/V_т. (6.3);

Теоретическая подача компрессора (м³/с) определяется по формуле

V_m= (πD² /4)(Sn), (6.4)

где D — диаметр цилиндра, м; S — ход поршня, м; п — частота вращения вала, об/с.

Коэффициент подачи компрессора может быть найден по формуле

η_V=η_обη_рη_тη_ут, (6.5)

где η_р — коэффициент, учитывающий уменьшение давления газа при всасывании вследствие сопротивления системы всасывания; η_т — коэффициент, учитывающий увеличение температуры газа от нагревания его при контакте со стенками цилиндра; η_ут — коэффициент, учитывающий утечки газа через неплотности во всасывающих клапанах.

Если известны давление и температура всасываемого газа р₀ и T₀ и параметры газа в начале сжатия в цилиндре р₁ и T₁, то коэффициенты η_p и η_m определяются по формулам:

η_p=p₁/p₀, (6.6)

η_m=T₀/T₁. (6.7)

Коэффициент, учитывающий утечки газа через неплотности:

. (6.8)

где G_вс и G_ут — расход всасываемого газа и расход на утечки в процессе сжатия и нагнетания, кг/с.

Массовая подача компрессора (кг/с) определяется по формуле

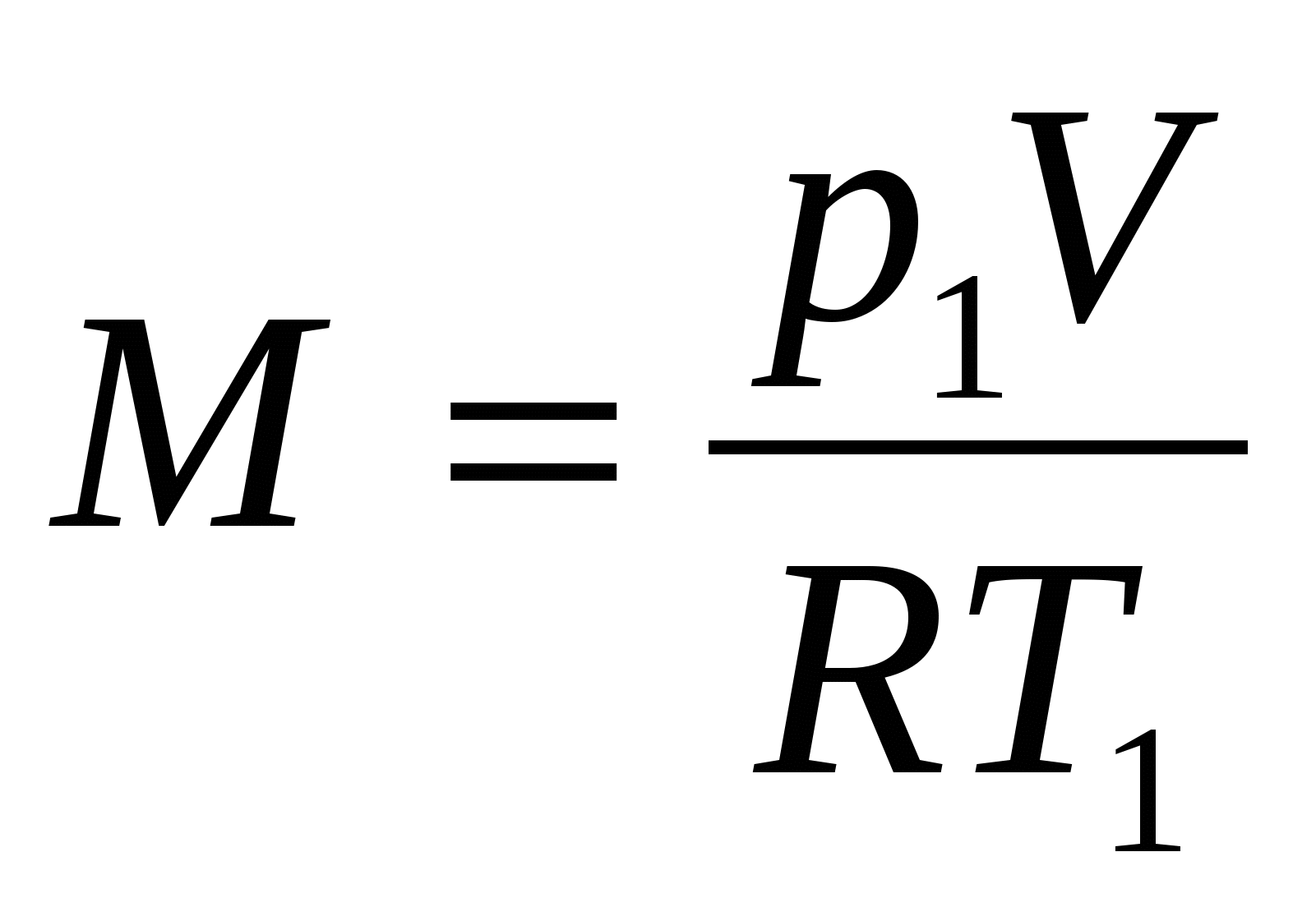, (6.9)

где р₁ — давление всасывания, Па;

V — действительная подача компрессора при давлении всасывания, м³/с;

R — газовая постоянная, Дж/(кг·К);

Т₁ — абсолютная температура газа на всасывании, К.

Теоретическая мощность (кВт) привода компрессора при изотермическом сжатии

. (6.10)

Теоретическая мощность (кВт) привода компрессора при адиабатном сжатии

, (6.11)

где k — показатель адиабаты.

Теоретическая мощность (кВт) привода компрессора при политропном сжатии

, (6.12)

где т — показатель политропы.

Эффективная мощность (кВт) привода компрессора с охлаждением

N_e=N_из/η_е.из, (6.13)

где η_е.из — изотермический эффективный кпд компрессора.

Эффективная мощность (кВт) привода компрессора без охлаждения

N_e=N_ад/η_е.ад, (6.14)

где η_е.ад — адиабатный эффективный кпд компрессора.

Эффективный кпд компрессора

η_е.из = η_изη_м; η_е.ад = η_адη_м, (6.15)

где η_из и η_ад — соответственно изотермический и адиабатный индикаторные кпд компрессора;

η_м — механический кпд компрессора (η_м= 0,85...0,95).

Индикаторная или внутренняя мощность (кВт) поршневого компрессора

N_i=p_iV_hn /10³, (6.16)

где p_i — среднее индикаторное давление, Па;

V_h — рабочий объем цилиндра, м³;

п — частота вращения вала, об/с.

Эффективная мощность компрессора (кВт)

N_e=N_i/η_м. (6.17)

Степень повышения давления в каждой ступени многоступенчатого компрессора может быть определена по формуле

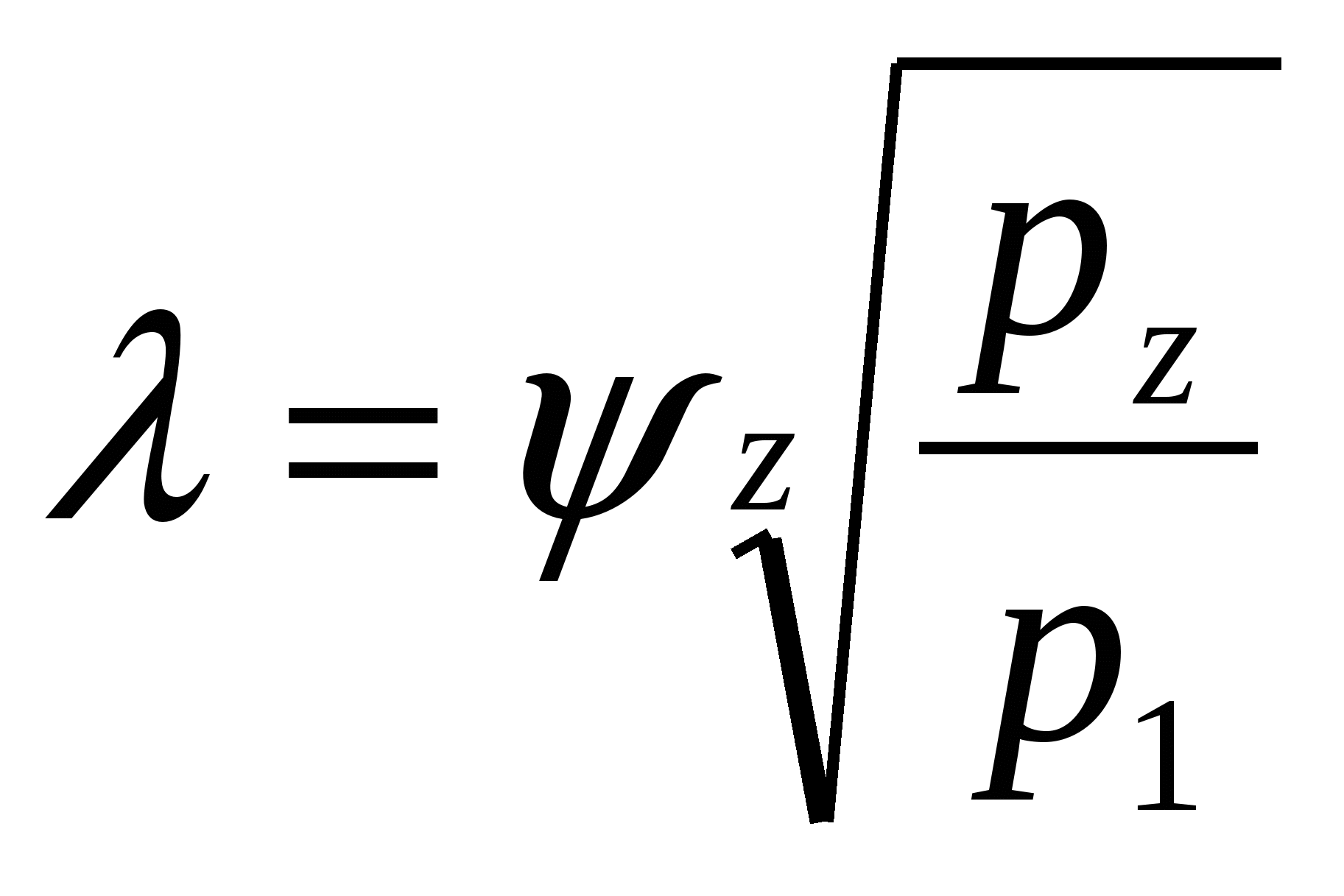, (6.18)

где z — число ступеней компрессора;

р_z — давление газа на выходе из последней ступени, Па;

р₁ — давление газа на входе в первую ступень, Па;

ψ =1,1...1,15 — коэффициент, учитывающий потери давления между ступенями.

Ротационные пластинчатые компрессоры. Теоретическая подача компрессора (м³/с) определяется по формуле

V_m =2 el (πD – zδ) n, (6.19)

где е — эксцентриситет, м;

l — длина ротора, м;

D — внутренний диаметр корпуса, м;

z — число пластин;

δ — толщина пластины, м;

n — частота вращения вала, об/с.

Действительная подача компрессора (м³/с) находится по формуле

V= 2 η_Vel (πD -zδ)n, (6.20)

где η_V — коэффициент подачи компрессора.

Теоретическая и эффективная мощности привода компрессора с охлаждением определяются по формулам (6.10), (6.13), а компрессора без охлаждения — по формулам (6.11) и (6.14).

Центробежные компрессоры.

Адиабатный кпд компрессора определяется по формуле

, (6.21)

где η_пол — политропный кпд компрессора, характеризующий совершенство проточной части компрессора как с охлаждением, так и без него (η_пол= 0,78...0,82).

Эффективная мощность (кВт) привода компрессора

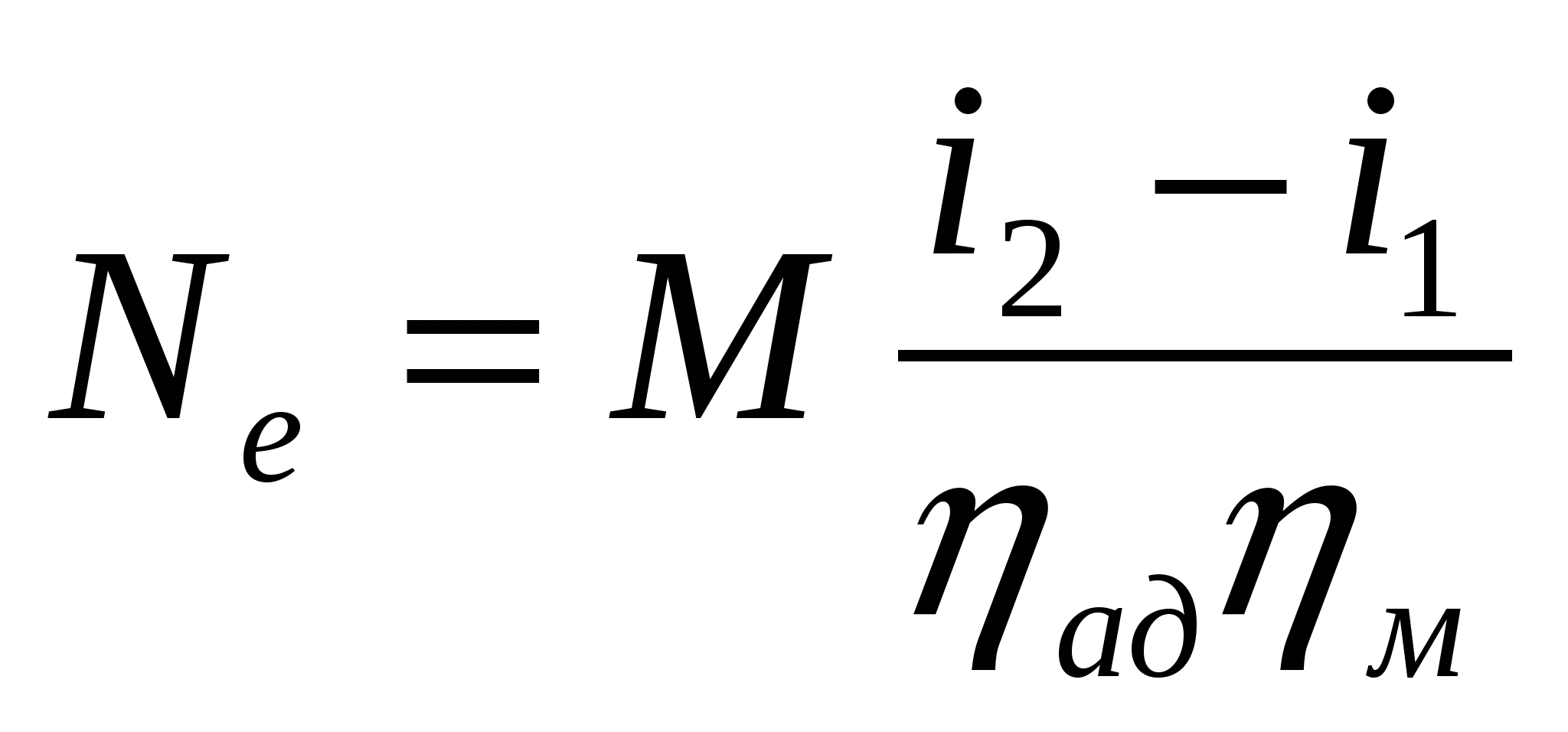, (6.22)

где i₂ и i₁ — соответственно энтальпия газа в конце адиабатного сжатия в компрессоре и у входа на лопатки колеса первой ступени, кДж/кг; М — массовая подача компрессора, кг/с.

Пример 1. Одноцилиндровый одноступенчатый поршневой компрессор сжимает воздух от давления p₁= 1·10⁵ Па до р₂ =7·10⁵Па. Определить эффективную мощность привода компрессора и необходимую мощность электродвигателя с запасом 10% на перегрузку, если диаметр цилиндра D =0,3 м, ход поршня S =0,3 м, частота вращения вала n =12 об/с, относительный объем вредного пространства σ=0,05, показатель политропы расширения остающегося во вредном объеме газа т= 1,3, коэффициент, учитывающий уменьшение давления газа при всасывании, η_р =0,94 и эффективный адиабатный кпд компрессора η_{е . ад} =0,75.

Решение: Степень повышения давления определяем по формуле (6.2):

λ = р₂ / р₁ =7·10⁵/(1·10⁵)=7.

Объемный кпд компрессора, по формуле (6.1),

=0,827.

Коэффициент подачи компрессора, по формуле (6.5),

η_V=η_обη_р= 0,827·0,94=0,777.

Теоретическая подача компрессора, по формуле (6.4),

V_m= (πD² /4)(Sn)=(3,14·0,3²/4)(0,3·12)=0,254 м³/с.

Действительная подача компрессора, из формулы (6.3),

V=V_тη_V= 0,254·0,777=0,197 м³/с.

Теоретическая мощность привода компрессора при адиабатном сжатии, по формуле (6.11),

=51 кВт.

Эффективная мощность привода компрессора, по формуле (6.14),

N_e=N_ад/η_е.ад =51/0,75=68 кВт.

Необходимая мощность электродвигателя с 10%-ным запасом перегрузки

N_эд= 1,1·68=74,8 кВт.

Пример 2. Одноступенчатый поршневой компрессор всасывает воздух при давлении p₁= 1·10⁵Па и температуре t₁= 17°С и сжимает его до давления р₂ =7·10⁵Па. Определить теоретическую мощность привода компрессора при изотермическом, адиабатном и политропном сжатии, если массовая подача компрессора M =0,12 кг/с и показатель политропы т= 1,3.

Решение: Степень повышения давления определяем по формуле (6.2):

λ = р₂ / р₁ =7·10⁵/(1·10⁵)=7.

Действительная подача компрессора при всасывании, из формулы (6.9),

V= MRT₁ / p₁ =0,12·287·290/(1·10⁵)=0,lм³/с.

Теоретическая мощность привода компрессора при изотермическом сжатии, по формуле (6.10),

=19,4 кВт.

Теоретическая мощность привода компрессора при адиабатном сжатии, по формуле (6.11),

=25,9 кВт.

Теоретическая мощность привода компрессора при политропном сжатии, по формуле (6.12),

= 24,2 кВт.

Пример 3. Одноцилиндровый одноступенчатый поршневой компрессор сжимает воздух от давления p₁ =1·10⁵Па до р₂= 3,5·10⁵Па. Определить действительную подачу компрессора, если диаметр цилиндра D =0,2 м, ход поршня S =0,15 м, частота вращения вала n =16 об/с, относительный объем вредного пространства σ=0,045, показатель политропы расширения газа, остающегося во вредном объеме, т =1,1 и коэффициент, учитывающий уменьшение давления газа при всасывании, η_р =0,95.

Решение: Степень повышения давления определяем по формуле (6.2):

λ = р₂ / р₁ =3,5·10⁵/(1·10⁵)=3,5.

Объемный кпд компрессора, по формуле (6.1),

=0,90.5.

Коэффициент подачи компрессора, по формуле (6.5),

η_V=η_обη_р= 0,905·0,95=0,86.

Теоретическая подача компрессора, по формуле (6.4),

V_m= (πD² /4)(Sn)=(3,14·0,2²/4)(0,15·16)=0,075 м³/с.

Действительная подача компрессора, из формулы (6.3),

V=V_тη_V= 0,075·0,86=0,0645 м³/с.

Пример 4. Двухцилиндровый двухступенчатый поршневой компрессор сжимает воздух от давления p₁= 1·10⁵ Па до р₂= 13·10⁵Па. Определить действительную подачу компрессора, если диаметр цилиндра D =0,3 м, ход поршня S =0,2 м, частота вращения вала n =14 об/с, относительный объем вредного пространства σ=0,05, показатель политропы расширения остающегося во вредном объеме газа т =1,25, коэффициент, учитывающий потери давления между ступенями, ψ =1,1 и коэффициент, учитывающий уменьшение давления газа при всасывании, η_p =0,94.

Решение: Степень повышения давления в каждой ступени определяем по формуле (6.18):

=3,9.

Объемный кпд, по формуле (6.1),

=0,901.

Коэффициент подачи, по формуле (6.5),

η_V=η_обη_р= 0,901·0,94=0,847.

Теоретическая подача ступени компрессора, по формуле (6.4),

V_m= (πD² /4)(Sn)=(3,14·0,3²/4)(0,2·14)=0,198 м³/с.

Действительная подача компрессора, из формулы (6.3),

V=V_тη_V= 20,198·0,847=0,335 м³/с.

Пример 5. Одноступенчатый центробежный компрессор с массовой подачей M =10 кг/с сжимает фреоновый пар от давления p₁ =1,6·10⁵ Па до p₂ =8,26·10⁵ Па. Определить эффективную мощность привода компрессора, если энтальпия пара у входа на лопатки колеса ступени i₁ =570 кДж/кг, энтальпия пара в конце адиабатного сжатия в компрессоре i₂ =600 кДж/кг, показатель адиабаты фреона-12 k =1,14, политропный кпд компрессора η_пол =0,78 и механический кпд компрессора η_м =0,95.

Решение: Степень повышения давления определяем по формуле (6.2):

λ = р₂ / р₁ =8,26·10⁵/(1,6·10⁵)=5,16.

Адиабатный кпд компрессора, по формуле (6.21),

=0,75.

Эффективная мощность привода компрессора, по формуле (6.22),

=421 кВт.

Пример 6. Определить эффективную мощность трехцилиндрового двухступенчатого компрессора с диаметрами цилиндров D₁ =0,2 м и D₂ =0,15 м и ходом поршней S =0,15 м, если частота вращения вала n =840 об/мин, механический кпд компрессора η_м =0,87, среднее индикаторное давление в первой ступени р_i1 =1,7·10⁵Па, во второй р_i2 =3,5·10⁵Па.

Решение: Индикаторную мощность цилиндра первой ступени сжатия N_i1 и второй – N_i2 определяем по формуле (6.16):

N_i1=p_i1V_h1n /10³ =p_i1πD 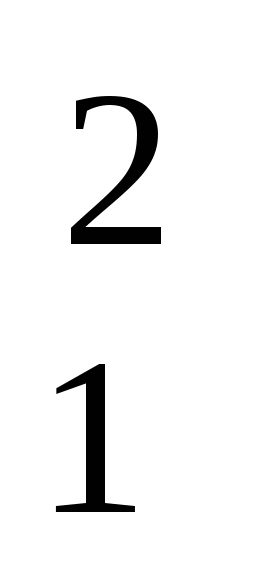Sn /(10³·4)=1,7·10⁵·3,14·0,2²·0,15·14/(1000·4)=11,2 кВт;

N_i2=p_i2V_h2n /10³ =p_i2πD Sn /(10³·4)=3,5·10⁵·3,14·0,15²·0,15·14/(1000·4)=13 кВт.

Индикаторная мощность компрессора

N_i=N_i1+N_i2 =2·11,2+13=35,4 кВт.

Эффективная мощность компрессора, по формуле (6.17),

N_e=N_i/η_м =35,4/0,87=40,7 кВт.

Задача 1. Одноступенчатый поршневой компрессор работает со степенью повышения давления λ =10 и с показателем политропы расширения газа, остающегося во вредном объеме, m =1,3. Определить коэффициент подачи компрессора, если относительный объем вредного пространства σ=0,04, коэффициент, учитывающий уменьшение давления газа при всасывании, η_p= 0,975, коэффициент, учитывающий увеличение температуры газа от нагревания его при контакте со стенками цилиндра, η_т =0,96 и коэффициент, учитывающий утечки газа через неплотности, η_ут =0,98.

 

Задача 2. Одноступенчатый поршневой компрессор работает со степенью повышения давления λ =3,5 и с показателем политропы расширения воздуха, остающегося во вредном объеме, т =1,1. Определить объемный кпд и коэффициент подачи компрессора, если относительный объем вредного пространства σ =0,045, параметры всасываемого воздуха р₀ =1·10⁵Пa и t₀ =25°С, параметры начала сжатия р₁= 0,98·10⁵Па и t₁=36°С, расход всасываемого воздуха G_вс =0,12кг/с и воздуха, идущего на утечки, G_ут =0,0024 кг/с.

 

Задача 3. Одноступенчатый поршневой компрессор работает со степенью повышения давления λ =7 и с показателем политропы расширения газа, остающегося во вредном объеме, т =1,3. Определить действительную подачу компрессора, если диаметр цилиндра D =0,2 м, ход поршня S =0,18 м, частота вращения вала n =900 об/мин, относительный объем вредного пространства σ =0,05, и коэффициент, учитывающий уменьшение давления газа при всасывании, η_р =0,92.

 

Задача 4. Одноступенчатый поршневой компрессор всасывает V =0,05 м³/с воздуха при давлении p₁ =1·10⁵Па и сжимает его до давления p₂ =8·10⁵Па. Определить теоретическую мощность привода компрессора при изотермическом, адиабатном и политропном сжатии с показателем политропы т =1,2.

Задача 5. Одноступенчатый поршневой компрессор с массовой подачей М =0,18кг/с всасывает воздух при давлении p₁= 1·10⁵ Па и температуре t₁= 20°Cи сжимает его до давления р₂ =6·10⁵Па. Определить, на сколько возрастет теоретическая мощность привода компрессора, если изотермическое сжатие воздуха в компрессоре будет заменено адиабатным.

Задача 6. Од оступенчатый поршневой компрессор с массовой подачей М =0,21кг/с сжимает воздух до давления р₂ =8·10⁵ Па. Определить эффективную мощность привода компрессора, если параметры всасывания p₁= 1·10⁵ Па и t₁= 20°С и эффективный изотермический кпд компрессора η_{е . из} =0,68.

Задача 7. Двухцилиндровый одноступенчатый поршневой компрессор сжимает воздух от давления p₁= 1·10⁵ Па до р₂= 6·10⁵Па. Определить эффективную мощность привода компрессора, если диаметр цилиндра D= 0,2м, ход поршня S =0,22 м, частота вращения вала п =440 об/мин, коэффициент подачи компрессора η_V= 0,82 и эффективный изотермический кпд компрессора η_{е . из} =0,12.

Задача 8. Определить, на сколько процентов уменьшится мощность, потребляемая поршневым компрессором, адиабатно сжимающим воздух от давления p₁= 1·10⁵ Па до р₂= 8·10⁵Па, при переходе от одноступенчатого к двухступенчатому сжатию.

Задача 9. Двухступенчатый компрессор с подачей V =0,2 м³/с сжимает воздух от давления p₁= 1·10⁵ Па до р₂ =30·10⁵Па. Определить эффективную мощность привода компрессора, если эффективный адиабатный кпд компрессора η_е.ад =0,69 и коэффициент, учитывающий потери давления между ступенями, ψ =1,1.

Задача 10. Трехступенчатый компрессор с массовой подачей М= 0,238 кг/с сжимает воздух от давления р₂ =112,5·10⁵Па. Определить эффективную мощность привода компрессора, если параметры всасывания воздуха p₁ =0,9·10⁵ Па и t₁ =17°С, коэффициент, учитывающий потери давления между ступенями, ψ =1,11, механический кпд компрессора η_м =0,94 и изотермический кпд компрессора η_из =0,7.

Задача 11. Определить индикаторную мощность двухцилиндрового двухступенчатого компрессора с диаметрами цилиндра D₁ =0,35 м и D₂ =0,2 м и ходом поршней S =0,2 м, если частота вращения вала n =12 об/с, среднее индикаторное давление в первой ступени р_i1 =1,2·10⁵Па, во второй р_i2 =3,4·10⁵Па.

Задача 12. Определить среднее индикаторное давление в ступенях двухцилиндрового двухступенчатого компрессора с диаметрами цилиндров D₁ =0,3 м и D₂ =0,18 м и ходом поршней S =0,15 м, если частота вращения вала п =13 об/с, индикаторная мощность цилиндра первой ступени N_i1 =25 кВт, второй ступени — N_i2 =26кВт.

Задача 13. Определить механический кпд двухцилиндрового двухступенчатого компрессора с диаметрами цилиндров D₁ =0,198 м и D₂ =0,155 м и ходом поршней S =0,145м, если частота вращения вала n =900 об/мин, эффективная мощность N_e =28,4 кВт, среднее индикаторное давление в первой ступени р_i1 =1,7·10⁵Па, во второй - р_i2 =3,5·10⁵Па,

Задача 14. Компрессор всасывает воздух при давлении p₁ =1·10⁵ Па и температуре t₁= 20°Cи сжимает его изотермически до давления p₂ =10·10⁵ Па. Определить эффективный изотермический кпд компрессора, если эффективная мощность привода компрессора N_e =57,6 кВт и массовая подача компрессора М =0,2 кг/с.

Задача 15. Определить теоретическую и действительную подачи одноступенчатого пластинчатого ротационного компрессора, если внутренний диаметр корпуса D =0,25 м, диаметр ротора d= 0,22 м, длина ротора l =0,45 м, число пластин z =15, толщина пластин δ =0,002 м, эксцентриситет е =0,015 м, окружная скорость вращения вала v =14,5 м/с и коэффициент подачи компрессора η_V= 0,75.

Задача 16. Двухступенчатый пластинчатый ротационный компрессор с подачей V =1,67 м³/с сжимает воздух от давления p₁ =1·10⁵ Па до p₂ =9·10⁵ Па. Определить эффективную мощность привода компрессора, если степень повышения давления в обеих ступенях одинаковая при полном промежуточном охлаждении воздуха. Эффективный изотермический кпд компрессора η_e.из =0,7.