Определение 1.Сферой с центром в точке O и радиусом r называют множество точек, расстояние от которых до точки O равно r (рис. 1).
Определение 2.Шаром с центром в точке O и радиусом r называют множество точек, расстояние от которых до точки O не превосходит r (рис. 1).
Рис.1
Таким образом, сфера с центром в точке O и радиусом r является поверхностью шара с центром в точке O и радиусом r.
Замечание.Радиусом сферы (радиусом шара) называют отрезок, соединяющий любую точку сферы с центром сферы. Длину этого отрезка также часто называют радиусом сферы (радиусом шара).
Определение 3.Сферическим поясом (шаровым поясом) называют часть сферы, заключенную между двумя параллельными плоскостями (рис. 2).
Определение 4.Шаровым слоем называют часть шара, заключенную между двумяпараллельными плоскостями (рис. 2).
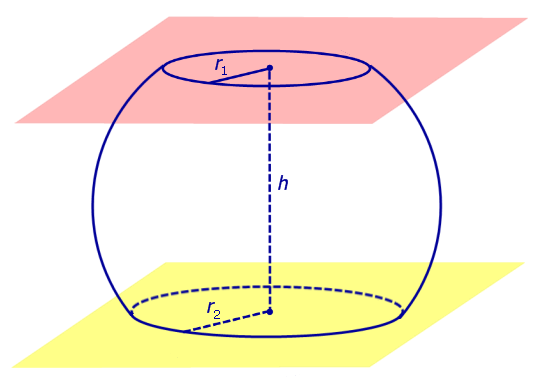
Рис.2
Окружности, ограничивающие сферический пояс, называют основаниями сферического пояса.
Расстояние между плоскостями оснований сферического пояса называют высотой сферического пояса.
Из определений 3 и 4 следует, что шаровой слой ограничен сферическим поясом и двумя кругами, плоскости которых параллельны между собой. Эти круги называют основаниями шарового слоя.
Высотой шарового слоя называют расстояние между плоскостями оснований шарового слоя.
Определение 5.Сферическим сегментом называют каждую из двух частей, на которые делит сферу пересекающая ее плоскость (рис. 3).
Определение 6.Шаровым сегментом называют каждую из двух частей, на которые делит шар пересекающая ее плоскость (рис. 3).
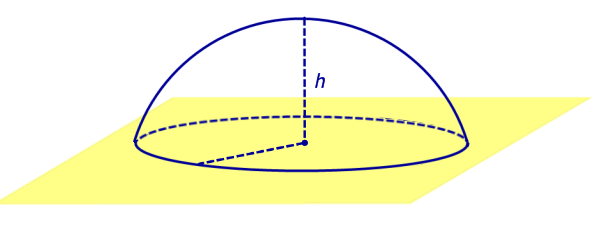
Рис.3
Из определений 3 и 5 следут, что сферический сегмент представляет собой сферический пояс, у которого одна из плоскостей оснований касается сферы (рис. 4).Высоту такого сферического пояса и называют высотой сферического сегмента.
|
|
Соответственно, шаровой сегмент – это шаровой слой, у которого одна из плоскостей оснований касается шара (рис. 4).Высоту такого шарового слоя называют высотой шарового сегмента.
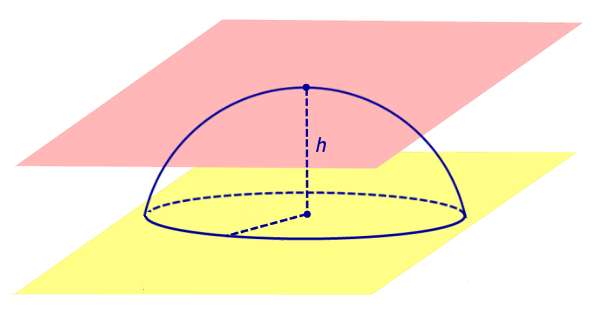
Рис.4
По той же причине всю сферу можно рассматривать как сферический пояс, у которого обе плоскости оснований касаются сферы (рис. 5).Соответственно, весь шар – это шаровой слой, у которого обе плоскости оснований касаются шара (рис. 5).
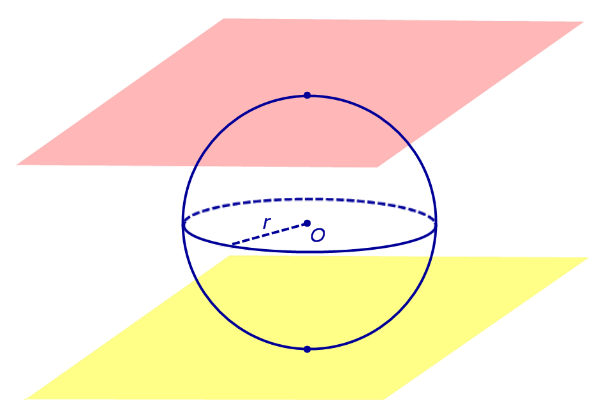
Рис.5
Определение 7.Шаровым сектором называют фигуру, состоящую из всех отрезков, соединяющих точки сферического сегмента с центром сферы (рис. 6).
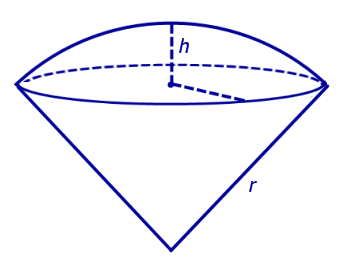
Рис.6
Высотой шарового сектора называют высоту его сферического сегмента.
Замечание. Шаровой сектор состоит из шарового сегмента и конуса с общим основанием. Вершиной конуса является центр сферы.
В следующей таблице приведены формулы, позволяющие вычислить объем шара и объемы его частей, а также площадь сферы и площади ее частей.
| Фигура | Рисунок | Формула | Описание |
| Сфера | 
| S = 4π r 2, где r – радиус сферы. | Площадь сферы |
| Шар |  где r – радиус сферы.
| Объем шара | |
| Сферический пояс |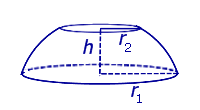 
| S = 2π rh, где r – радиус сферы, h – высота сферического пояса. | Площадь сферического пояса |
| Шаровой слой |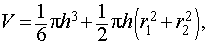 
где r 1, r 2 – радиусы оснований шарового слоя, h – высота шарового слоя.
| Объем шарового слоя | |
| Сферический сегмент |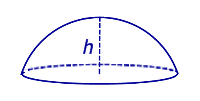 
| S = 2π rh, где r – радиус сферы, h – высота сферического сегмента. | Площадь сферического сегмента |
| Шаровой сегмент | 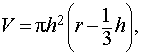 где r – радиус сферы, h – высота шарового сегмента.
| Объем шарового сегмента | |
| Шаровой сектор | 
| 
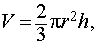где r – радиус сферы, h – высота шарового сектора.
| Объем шарового сектора |
|
|