Влияние зазора и натяга в рабочих органах винтового насоса на его характеристики

 

Рассмотрим явления, связанные с зазорами и натягами, имеющимися в на­со­се [14].

Практика проектирования насосов с упругой обоймой показы­вает, что для обес­печения эффективной работы необходимо со­здать достаточную гер­ме­тич­ность по линиям контакта поверхностей винта и обоймы. Обычно герме­тич­ность достигается тем, что рабочий винт имеет превышение одного или нес­коль­ких размеров (чаше всего поперечного сечения) над соответствующими эле­мен­тами профиля обоймы, т.е. имеет место первоначальный натяг δ₀.

Схема действующих сил. Определим силы, вызывающие тре­ние, винта и рег­ламентирующие положение винта в обойме (рис. 1.175). Таких сил две.

1. Сила инерции, существование которой обусловлено кине­матикой дви­же­ния винта, на длине шага винта

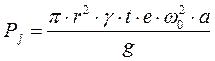(1.50)

где r — радиус поперечного сечения винта;

t — шаг винта;

е — эксцентриситет винта;

γ — удельный вес материала винта;

ω ₀ — угловая скорость перемещения оси винта относительно оси обоймы;

g — ускорение силы тяжести;

α — коэффициент, учитывающий силу инерции от вращения эксцент­ри­ко­вой муфты и той части тела винта, которая высту­пает из обоймы.

2. Радиальная гидравлическая сила, определенная Д.Д. Саввиным:

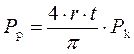(1.51)

Риг. 1.175. Схема действия сил в насосе

 

Здесь P _k — межвитковый перепад давления.

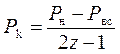(1.52)

где P _н — давление нагнетания;

Р _вс— давление всасывания;

z — количество шлюзов в каждой нарезке обоймы.

Равнодействующая этих двух сил равна:

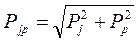(1.53)

Суммарная нормальная сила на контактной линии на длине шага винта:

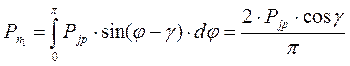(1.54)

Из рис. 1.175 видно, что угол φ является углом поворота оси сечения обоймы относительно оси z, а γ = arctg (Р_p / Р_j).

Таким образом, устанавливаем, что нормальная сила, прижи­мающая винт к обой­ме, является функцией обеих радиальных сил, а также соотношением их зна­чений.

Приведенная нормальная сила с учетом влияния первоначаль­ного натяга

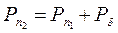. (1.55)

где сила Р_δ является функцией первоначального натяга, тол­щины и меха­ни­чес­ких свойств резины рабочей поверхности обой­мы и определяется экспери­мен­таль­но.

Деформация внутренней поверхности обоймы происходит в направлении рав­но­действующей силы Р_jp, под действием ко­торой винт смещается в обойме. Предположим, что смещение это (ОО₁) будет равно m (рис. 1.176) изменится и натяг (радиаль­ная деформация резины) на контактной поверхности рабочих органов.

Суммарный натяг представим в виде:

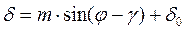(1.56)

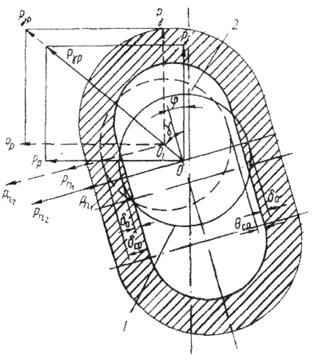
Рис. 1.176. Деформации обоймы

С целью создания смазки на контактной поверхности гeoметрические раз­ме­­ры рабочих органов выбираются таким образом, чтобы обеспечить при ра­бо­те насоса появление зазора.

Знамения зазора определяются

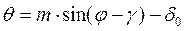. (1.57)

Уравнении (1.56) и (1.57) справедливы для всех положении винта в обой­ме, за исключением момента φ = 0 ± (π /2) n, когда сечение винта занимает крайнее положение в сечении обоймы. Анализ деформации резины в этих сечениях показывает, что образующийся после деформации затор весьма мал и для практи­ческих расчетов им можно пренебречь. Графики изменения затора и натяга на развертке рабочих органов насоса на длине шага обоймы показаны на рис. 1.177

Рис. 1.177. Схема развертки контактных линий рабочих органов:

а — нарезка I; б — нарезка II:

1 — первоначальный натяг; 2 — радиальная деформация резины в направ­лении равно­дейст­вую­щей Р_jp, 3 — действительное значение зазора и натя­га; 4 — усредненные значения за­зо­ра; 5 — усредненные значении натяга

 

Исследование зависимостей (1.56) и (1.57) показывает, что ввиду малой амплитуды кривых справедливо, при сохранении постоянства гидравлического радиуса, заменить действительные значения зазора и натяга средними, поль­зуясь следующими выражениями:

 

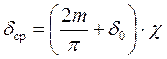, (1.58)

где χ — коэффициент,

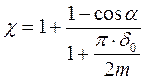
здесь 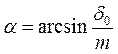(1.59)

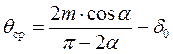
Длина проекции проточной части контактной линии на ось обоймы на длине шага винта

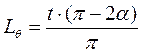(1.60)

Длина проекции поверхности трения винта в обойме по длине шага винта

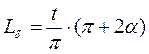. (1.61)

На основании проведенных исследований были сделаны сле­дующие выводы:

1. Одновинтовой насос характеризуется непостоянной ори­ентацией рабо­че­го винта. При работе насоса под действием инер­ционных и гидравлических сил происходит радиальная дефор­мация упругой обоймы и смешение винта в по­перечном направ­лении.

2. Деформация обоймы предопределяет возникновение зазо­ра с одной сто­ро­ны, диаметрального сечения винта и натяга между винтом и обоймой с дру­гой, величина и протяженность которых непостоянны и определяются выра­же­ния­ми (1.56—1.61).

Механические потери. Первоначально примем два допущения.

1. В процессе работы насоса винт самоустанавливается с обой­ме, вследст­вие чего силы, действующие на обойму, распределя­ются равномерно по всей дли­не (при идеальной геометрии винта и обоймы).

2. Коэффициент трения винта по резиновой поверхности обой­мы постоя­нен.

Мощность трения на длине обоймы, кВт:

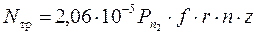, (1.62)

где f — коэффициент трения пары «обойма — винт», в фун­кции удельного давления;

n — скорость вращения приводного вала, об/мин.

Задачей одного из циклов проведенных балансовых испыта­ний являлось опре­деление области оптимальных значений ве­личины δ_о. Было установлено, что для обойм, внутренняя полость которых отлита из резины с твердостью 55—75 ед. по ТМ-2, оптимальным с точки зрения равномерности расп­ре­де­ле­ния дав­ления вдоль оси обоймы следует считать межвитковый перепад дав­ле­ния

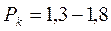кг/см². (1.63)

В этом режиме максимальные уровни КПД были получены при следующих значениях величины первоначального натяга

δ _{0 опт} = (0,02 ­– 0,03) ч. (1.64)

Механические потери в рабочих органах существенно зави­сят от величины первоначального натяга (рис. 1.178).

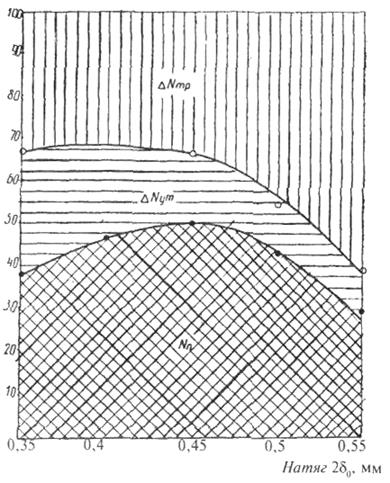
Рис. 1.178. Зависимость энергетических показателей насоса IBB 0,4/2 от величины первоначального натяга

 

При δ₀ > δ_{0 опт} наблюдается резкое повышение мощности трения.

Объемные потери. Объемные потери представляют собой рас­ход жид­кос­ти через щель проточной части контактной поверх­ности:

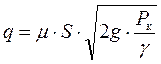, (1.65)

где S — площадь щели.

Коэффициент расхода μ в общем виде является функцией исла Рейнольдса

,

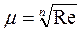определяемого из выражения

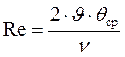, (1.66)

где v — коэффициент кинематической вязкости.

Совместно решая уравнения (1.62) и (1.63), получим:

где Е — длина проточной части контактной линии.

Для определенного типоразмера насоса при перекачке одно­родных жид­кос­тей произведены

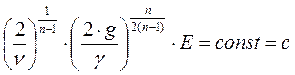. (1.68)

Следовательно,

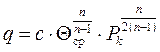(1.69)

Стендовые испытания рабочих органов насоса 1ВВ 1,6; 1ВВ 0,8 и 1BB 0,4 при перекачке воды показали, что при перво­начальных натягах по выражению (1.61) перетоки жидкости ха­рактеризуются весьма широким диапазоном числа Рейнольдса (Re = 300—10000).

Экспериментально были получены следующие значения ко­эффициентов:

,

.

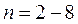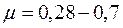Анализ выражения (1.69) (предположив Р _к = const) позволяет получить ана­ли­тическую зависимость объемных потерь насоса от величины зазора и пер­во­начального натяга:

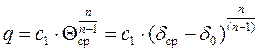, (1.70)

где 1,14 < 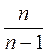< 2.

На рис. 1.179 показана зависимость объемных потерь насоса 1ВВ, 1,6/16 от ве­личины первоначального натяга при перекачке воды.

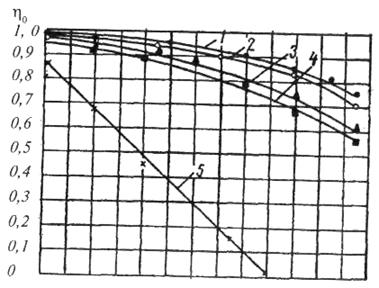
Рис. 1.179. Зависимость объемного КПД одновинтового насоса 1ВВ 1,6/16 от величины первоначального натяга δ ₀:

1 — 0,4 мм, 2 — 0,35 мм; 3 — 0,28 мм, 4 — 0,2 мм; 5 — натяг отсутствует

 

Анализ результатов испытаний объясняет заметный разброс значений по­да­чи насосов серийного производства, в которых по технологическим сообра­же­ниям первоначальный натяг имеет отклонение ± 0,1 мм.

Результаты теоретических и экспериментальных исследова­ний показали:

1. Величина первоначального натяга оказывает большое влияние на энер­ге­ти­ческие показатели одновинтовых насосов. Для принятых оптимальных зна­че­ний перепадов межвитковых давлений (1.61) имеет место интервал значений пер­воначально­го натяга (1.62), при котором рабочие органы насоса работают с мак­симальным значением КПД, достигающим 70—75 % для на­соса 1BB 1,6 и 55—65% для насоса 1ВВ 0,4

2. С повышением величины δ ₀уменьшается зазор в проточ­ной части кон­такт­ной линии, вследствие чего уменьшаются объемные потери; увеличивается нор­мальная сила и уменьшает­ся удельное давление, что вызывает увеличение ме­ханических потерь.

3. При натяге δ₀ > δ_{0 опт} наблюдается резкое понижение обще­го КПД насо­са.