ПОСТОЯННЫЙ ЭЛЕКТРИЧЕСКИЙ ТОК

Примеры решения задач

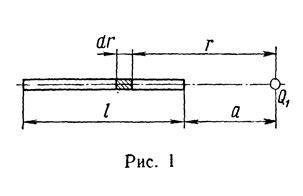
Пример 1. На тонком стержне длиной l = 20 см находится рав­номерно распределенный электрический заряд. На продолжении оси стержня на расстоянии а = 10 см от ближайшего конца находится то­чечный заряд q₁ = 40 нКл, который взаимодействует со стержнем с си­лой F = 6 мкН. Определить линейную плотность τ заряда на стержне.

Р е ш е н и е. Сила взаимодействия F заряженного стержня с точечным зарядом q₁ зависит от линейной плотности τ заряда на стержне. Зная эту зависимость, можно определить τ. При вычислении силы F следует иметь в виду, что заряд на стержне не является точеч­ным, поэтому закон Кулона непосредственно применить нельзя. В этом случае можно поступить следующим образом. Выделим из стержня (рис. 1) малый участок dr с зарядом dq = τdr. Этот заряд можно рас­сматривать как точечный. Тогда, согласно закону Кулона,

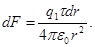
Интегрируя это выражение в пределах от 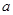до 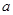+ 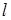, полу­чаем

 

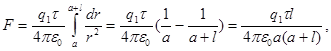откуда

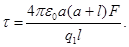
Проверим, дает ли расчетная формула единицу линейной плот­ности электрического заряда. Для этого в правую часть формулы вме­сто символов величин подставим их единицы:

 

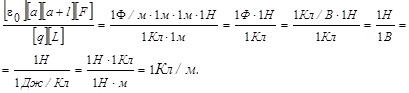
Найденная единица является единицей линейной плотности заряда.

Произведем вычисления:

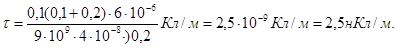
Пример 2. По тонкому кольцу равномерно распределен заряд q = 40 нКл с линейной плотностью τ = 50 нКл/м. Определить напря­женность электрического поля, создаваемого этим зарядом в точке А, лежащей на оси кольца и удаленной от его центра на расстоянии, равное половине радиуса.

 

 

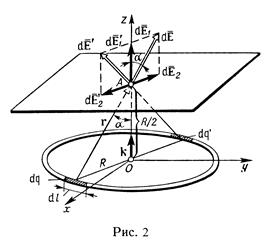
Р е ш е н и е. Совместим координатную плоскость xOy с плос­костью кольца, а ось Oz – с осью кольца (рис. 2). На кольце выделим малый участок длиной dl. Так как заряд dq=τdl, находящийся на этом участке, можно считать точечным, то напряженность d электриче­ского поля, создаваемого этим зарядом, может быть записана в виде

 

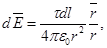
где – радиус-вектор, направленный от элемента dl к точке А.

Разложим вектор d на две составляющие: d ₁, перпендику­лярную плоскости кольца (сонаправленную с осью Oz), и d ₂, парал­лельную плоскости кольца (плоскости xOy), т. е.

.

Напряженность электрического поля в точке А найдем интегрированием:

где интегрирование ведется по всем элементам заряженного кольца. Заметим, что для каждой пары зарядов dq и dq` (dq = dq`), расположен­ных симметрично относительно центра кольца, векторы d ₂ и d ₂` в точке А равны по модулю и противоположны по направлению: d <sub>2</sub> = - d <sub>2</sub>`. Поэтому векторная сумма (интеграл) Составляю­щие d ₁ для всех элементов кольца сонаправлены с осью Oz (единич­ным вектором ), т. е. d ₁ = 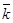dE₁. Тогда

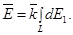
Так как 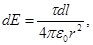и то

Таким образом,

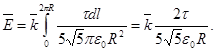
Из соотношения q = 2πRτ определим радиус кольца R = q/(2πτ). Тогда

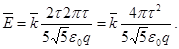
Модуль напряженности

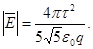(1)

Проверим, дает ли правая часть полученного равенства еди­ницу напряженности (В / м):

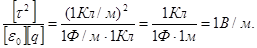
Выразим физические величины, входящие в формулу (1), в единицах СИ (τ = 5·10^-8 Кл/м, q=4·10^-8 Кл, ε₀ = 8,85·10^-12 Ф/м) и произ­ведем вычисления:

 

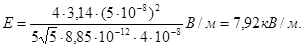
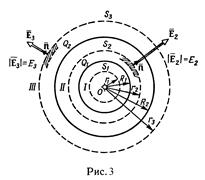Пример 3. Две концентрические проводящие сферы радиу­сами R₁ = 6 см и R₂ = 10 см несут соответственно заряды q₁ = 1нКл и q₂ = - 0,5нКл. Найти напряженность Е поля в точках отстоящих от цен­тра сфер на расстояниях r₁ = 5 см, r₂ = 9 см, r₃ = 15 см. Построить гра­фик E(r).

 

Р е ш е н и е. Заметим, что точки, в которых требуется найти напря­женности электрического поля, лежат в трех областях (рис. 3): об­ласти I (r₁<R₁), области II (R₁<r₂<R₂), области III (r₂>R₂).

1. Для определения напряженности Е₁ в области I проведем гаус­сову поверхность S₁ радиусом r₁ и воспользуемся теоремой Остроград­ского – Гаусса:

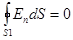
(так как суммарный заряд, находящийся внутри гауссовой поверхно­сти, равен нулю). Из соображений симметрии E_n=E₁=const. Следова­тельно, и Е₁ (напряженность поля в области I) во всех точ­ках, удовлетворяющих условию r₁<R₁, будет равна нулю.

2. В области II гауссову поверхность проведем радиусом r₂. В этом случае (диэлектрическую проницаемость среды будем считать равной единице (вакуум))

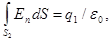
(так как внутри гауссовой поверхности находится только заряд q₁).

Так как E_n = E = const, то Е можно вынести за знак интеграла:

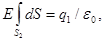или ES₂ = q₁/ .

Обозначив напряженность Е для области II через Е₂, получим

Е₂ = q₁/( S₂),

где S₂ = 4πr₂² – площадь гауссовой поверхности. Тогда

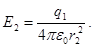(1)

3. В области III гауссова поверхность проводится радиусом r₃. Обозначим напряженность Е области III через Е₃ и учтем, что в этом случае гауссова поверхность охватывает обе сферы и, следовательно, суммарный заряд будет равен q₁ + q_2. Тогда

Е₃ = (q₁+q₂)/4π r₃².

Заметив, что q₂<0, это выражение можно переписать в виде

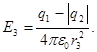(2)

Убедимся в том, что правая часть равенства (1) и (2)дает единицу на­пряженности:

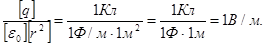
Выразим все величины в единицах СИ (q₁ = 10^-9 Кл, q₂= - 0,5·10^-9 Кл, r₁=0,09 м, r₂=0,15 м, 1/(4πε₀)=9·10⁹ м/Ф) и произведем вычисления:

Построим график E(r). В области I(r₁<R₁) Е = 0. В области II (R₁ r<R₂) E₂(r) изменяется по закону 1/r². В точке r = R₁ напряжен­ность E₂(R₁) = q₁/(4π R₁²)=2,25 кв/м. В точке r = R₂ (r стремится к R₂ слева) E₂(R₂) = q₁/(4π R₂²) = 0,9 кВ/м. В области III (r>R₂) E₃(r) изменяется по закону 1/r², причем в точке r = R₂ (r стремится к R₂ справа) E₃(R₂) = (q₁ - |q₂|/(4π R₂²) = 0,45 кВ/м. Таким образом, функ­ция E(r) в точках r = R₁ и r = R₂ терпит разрыв.

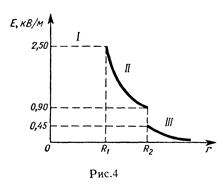
График зависимости E(r) представлен на рис. 4.

 

 

Пример 4. Электрическое поле создано длинным цилиндром радиусом R = 1 см, равномерно заряженным с линейной плотностью τ = 20 нКл/м. Определить разность потенциалов двух точек этого поля, находящихся на расстоянии 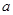₁ = 0,5 см и 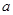₂ = 2 см от поверхности цилиндра, в средней его части.

Р е ш е н и е. Для определения разности потенциалов воспользуемся соотношением между напряженностью поля и измене­нием потенциала: 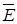= - grad φ. Для поля с осевой симметрией, каким является поле цилиндра, это соотношение можно записать в виде

E = - dφ/dr, или dφ = - Edr.

Интегрируя это выражение, найдем разность потенциалов двух точек, отстоящих на расстояниях r₁ и r₂ от оси цилиндра:

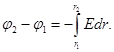
(1)

 

 

Так как цилиндр длинный и точки взяты вблизи его средней части, то для выражения напряженно­сти поля можно воспользоваться формулой напряженности поля, соз­даваемого бесконечно длинным цилиндром:

E = τ/(2π r).

Подставив выражение Е в (1), получим

или

φ₁ – φ₂ = τ/(2π )ln(r₂/r₁). (2)

Произведем подстановку, учитывая, что величины r₁ и r₂, входящие в формулу (2) в виде отношения, можно выразить в сантиметрах (r₁ = R + 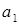= 1,5 см r₂ = R + 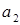= 3 см):

φ₁ – φ₂ = 2 · 10 ^–8 · 1,8 · 10¹⁰ ln(3/1,5) = 3,6 · 10² · 2,3 ln2 В = 250 В.

 

Пример 5. Конденсатор емкостью С₁ = 3 мкФ был заряжен до разности потенциалов U₁ = 40 В. После отключения от источника тока конденсатор соединили с другим незаряженным конденсатором емко­стью С₂ = 5 мкФ. Какая энергия 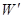израсходуется на образование искры в момент присоединения второго конденсатора?

Р е ш е н и е. Энергия, израсходованная на образование искры,

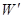= W₁ – W₂, (1)

где W₁ – энергия, которой обладает первый конденсатор до присоеди­нения к нему второго конденсатора; W₂ – энергия, которую имеет ба­тарея, составленная из двух конденсаторов.

Энергия заряженного конденсатора определяется по формуле

W = ½СU², (2)

где С – емкость конденсатора или батареи конденсаторов.

Выразив в формуле (1) энергии W₁ и W₂ по формуле (2) и при­няв во внимание, что общая емкость параллельно соединенных кон­денсаторов равна сумме емкостей отдельных конденсаторов, получим

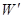= ½ C₁U₁² – ½(C₁ + C₂)U₂², (3)

где U₂ – разность потенциалов на зажимах батареи конденсаторов.

Учитывая, что заряд после присоединения второго конденса­тора остался прежним, выразим разность потенциалов U₂ следующим образом:

Подставив выражение U₂ в (3), найдем

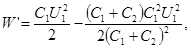
или

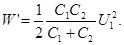
Произведем вычисления:

 

Расчетные задания №1

 

Номер варианта	Номера задач

1. Точечные заряды q₁=20 мкКл, q₂=-10 мкКл находятся на рас­стоянии d =5см друг от друга. Определить напряженность поля в точке, удаленной на r₁=3 см от первого и на r₂=4 см от второго за­ряда. Опре­делить также силу 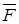, действующую в этой точке на точечный заряд q= 1 мкКл.

2. Три одинаковых точечных заряда q₁=q₂=q₃=2 нКл находятся в вершинах равностороннего тре­угольника со сторонами а =10см. Опре­делить модуль и направление силы 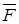, действующей на один из заря­дов со стороны двух других.

3. Два положительных точечных заряда q и 9q закреплены на рас­стоянии d=100см друг от друга. Определить, в какой точке на прямой, проходящей через заряды, следует поместить третий заряд так, чтобы он находился в равновесии. Указать, какой знак должен иметь этот заряд для того, чтобы равновесие было устой­чивым, если перемещения зарядов возможны только вдоль прямой, проходящей через закреп­ленные заряды.

4. Два одинаково заряженных шарика подвешены в одной точке на нитях одинаковой длины. При этом нити разошлись на угол a. Ша­рики погружают в масло. Како­ва плотность r масла, если угол расхож­дения нитей при погружении в масло остается неизменным? Плотность материала шариков r₀=1,5×10³ кг/м³, диэлектрическая проницаемость масла e = 2,2.

5. Четыре одинаковых заряда q₁= q₂=q₃=q₄=40кНл закреплены в вершинах квадрата со стороной а =10см. Найти силу 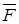, действую­щую на один из этих зарядов со стороны трех остальных.

6. Точечные заряды q₁=30 мкКл и q₂=-20 мкКл находятся на рас­стоянии d =20 см друг от друга. Опре­делить напряженность электриче­ского поля 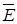в точке, удаленной от первого заряда на расстояние r₁ = 30 см, а от второго – на r₂ = 15 см.

7. В вершинах правильного треугольника со стороной а= 10 см находятся заряды q₁=10мкКл, q₂=20 мкКл и qз=30 мкКл. Определить силу 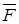, действую­щую на заряд q₁ со стороны двух других зарядов.

8. В вершинах квадрата находятся одинаковые заряды q₁=q₂=q₃=q₄= 8×10^-10 Кл. Какой отрица­тельный заряд q нужно поместить в центре квадрата, чтобы сила взаимного отталкивания положительных зарядов была уравновешена силой притяжения отрицательного заряда?

9. На расстоянии d=20 см находятся два точечных заряда: q₁=-50 нКл и q₂=100нКл. Определить силу 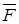, действующую на заряд q₃=-10 нКл, удаленный от обоих зарядов на одинаковое расстояние, равное d.

10. Расстояние d между двумя точечными зарядами q₁=2нКл и q₂=4нКл равно 60см. Определить точку, в которую нужно поместить третий заряд q₃ так, чтобы система зарядов находилась в равновесии. Определить заряд q₃ и его знак. Устойчивое или неустойчивое будет равновесие?

11. Тонкий стержень длиной l =20 см несет равномерно распреде­ленный заряд t=0,1 мкКл. Определить напряженность 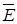электриче­ского поля, создаваемого распределенным зарядом в точке А, лежащей на оси стержня на расстоянии а=20 см от его конца.

12. По тонкому полукольцу радиуса R=10 см равномерно распре­делен заряд с линейной плотностью t = 1 мкКл/м. Определить напря­женность 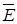электрического поля, создаваемого распределенным заря­дом в точке О, совпадающей с центром кольца.

13. Тонкое кольцо несет распределенный заряд q=0,2 мкКл. Оп­ределить напряженность 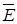электрического поля, создаваемого распределенным зарядом в точке A, равноудаленной от всех точек кольца на расстояние г=20 см. Радиус кольца R=10см.

14. Треть тонкого кольца радиуса R=10см несет распределенный заряд q=50нКл. Определить напряженность 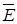электрического поля, создаваемого распре­деленным зарядом в точке О, совпадающей с цен­тром кольца.

15. Бесконечный тонкий стержень, ограниченный с одной сто­роны, несет равномерно распределенный заряд с линейной плотностью t=0,5 мкКл/м. Определить напряженность 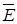электрического поля, создаваемого распределенным зарядом в точке А, лежащей на оси стержня на расстоянии а =20 см от его начала.

16. По тонкому кольцу радиусом R=20см равномерно распреде­лен с линейной плотностью t=0,2 мкКл/м заряд. Определить напря­женность 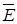электрического поля, создаваемого распределенным заря­дом в точке A, находящейся на оси кольца на расстоянии h=2R от его центра.

17. По тонкому полукольцу равномерно распределен заряд q=20 мкКл с линейной плотностью t=0,1 мкКл/м. Определить напря­женность 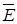электрического поля, создаваемого распределенным заря­дом в точке О, совпадающей с центром кольца.

18. Четверть тонкого кольца радиусом R=10см несет равномерно распределенный заряд q=0,05 мкКл. Определить напряженность 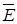электрического поля, создаваемого распределенным зарядом в точке О, совпа­дающей с центром кольца.

19. По тонкому кольцу равномерно распределен заряд q=10 нКл с линейной плотностью t=0,01 мкКл/м. Определить напряженность 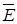электрического поля, создаваемого распределенным зарядом в точке А, лежащей на оси кольца и удаленной от его центра на расстояние, рав­ное радиусу кольца.

20. Две трети тонкого кольца радиусом R=10см несут равномерно распределенный с линейной плотностью t=0,2 мкКл/м заряд. Опреде­лить напряженность 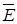электрического поля, создаваемого распределенным зарядом в точке О, совпадающей с центром кольца.

21. На двух концентрических сферах радиусом R и 2R равномерно распределены заряды с поверхностными плотностями s₁ и s₂ (рис. 5). Требуется: 1) используя теорему Остроградского-Гаусса, найти зави­симость E(r) напряженности электрического поля от расстояния для трех областей: I, II и III. Принять s₁=4s, s₂=s; 2) вычислить напряжен­ность Е в точке, удаленной от центра на расстояние r, и указать на­правление вектора 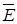.Принять s=30нКл/м², г= l,5R; 3) построить гра­фик E(r).

22. См. условие задачи 21. В п. 1 принять s₁=s, s₂=-s. В п. 2 при­нять s=0,1мкКл/м², r=3.

23. См. условие задачи 21. В п. 1 принять s₁=-4s, s₂=s. В п. 2 принять s=50 нКл/м², r=1,5R.

24. См. условие задачи 21. В п. 1 принять s₁=-2s, s₂=s. В п. 2 принять s=0,1мкКл/м², г==3R.

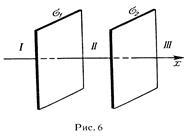
25. На двух бесконечных параллельных плоскостях равномерно распределены заряды с поверхностными плотностями s₁ и s₂ (рис. 6). Требуется: 1) используя теорему Остроградского-Гаусса и принцип суперпози­ции электрических полей, найти выражение Е(х) напря­жен­ности электрического поля в трех областях: I, II и III.Принять s₁=2s, s₂=s; 2) вычислить напряженность Е по ля в точке, расположенной слева от плоскостей, и указать направление вектора 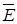; 3) построить график Е(х)

26. См. условие задачи 25. В п. 1 принять s₁=-4s, s₂=2s. В п. 2 принять s=40 нКл/м² и точку расположить между плоскостями.

27. См. условие задачи 25. В п. 1 принять s₁=s, s₂=-2s. В п. 2 принять s=20 нКл/м² и точку располо­жить справа от плоскостей.

28. На двух коак­сиальных бесконечных цилиндрах радиусами R и 2R равномерно распре­делены заряды с поверх­ностными плот­ностями s₁ и s₂ (рис. 7). Требу­ется:

1) используя теорему Ост­роградского-Гаусса, найти за­висимость Е(r) напряженности электри­ческого поля от расстоя­ния для трех областей: I, II и III. Принять s₁=-2, s₂=s; 2) вычис­лить напряженность Е в точке, удаленной от оси цилиндров на расстояние r, и указать направ­ление вектора 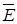. Принять s= 50нКл/м², r = 1,5R; 3) построить график E(r).

29. См. условие задачи 28. В п. 1 принять s₁=s, s₂=-s. В п. 2 при­нять s= 60нКл/м², r =3R.

30. См. условие задачи 28. В п. 1 принять s₁=-s, s₂=4s. В п. 2 принять s= 30нКл/м², r =4R.

31. Два точечных заряда q₁=6нКл и q₂=3нКлнаходятся на рас­стоянии d=60 см друг от друга. Какую работу необходимо совершить внешним силам, чтобы уменьшить расстояние между зарядами вдвое?

32. Электрическое поле создано заряженным проводящим шаром, потенциал j которого 300 В. Определить работу сил поля по переме­щению заряда q= 0,2мкКл из точки 1 в точку 2 (рис.8).

33. Электрическое поле создано зарядами q₁=2мкКл и q₂=-2мкКл, находящимися на расстояние а =10см друг от друга. Определить работу сил поля, совершаемую при перемещении заряда q=0,5мкКл из точки 1 в точку 2 (рис.9).

34. Две параллельные заряженные плоскости, поверхностные плотности заряда которых s₁=2мкКл/м² и s₂=-0,8мкКл/м², находятся на расстоянии d =0,6см друг от друга. Определить разность потенциалов U между плоскостями.

35. Диполь с электрическим моментом р = 100 пКл×м свободно установился в свободном электрическом поле напряженностью Е =200кВ/м. Определить работу внешних сил, которую необходимо совершить для поворота диполя на угол a=180°.

36. Четыре одинаковых капли ртути, заряженных до потенциала j=10В, сливаются в одну. Каков потен­циал j₁ образовавшейся капли?

37. Тонкий стержень согнут в кольцо радиусом R =10 см. Он рав­номерно заряжен с линейной плотностью заряда t=800нКл/м. Опреде­лить потенциал j в точке, расположенной на оси кольца на расстоянии h = 10см от его центра.

38. Поле образовано точечным диполем с электри­ческим момен­том р = 200пКл×м. Определить разность потенциалов U двух точек поля, расположенных симмет­рично относительно диполя на его оси на расстоянии r =40 см от центра диполя.

39. Электрическое поле образовано бесконечно длин­ной заряжен­ной нитью, линейная плотность заряда кото­рой t= 20пКл/м. Опреде­лить разность потенциалов U двух точек поля, отстоящих от нити на расстоянии r₁=8см и r₂= 12см.

40. Тонкая квадратная рамка равномерно заряжена с линейной плотностью заряда t=200пКл/м. Опреде­лить потенциал j поля в точке пересечения диагоналей.

41. Пылинка массой т =200мкг, несущая на себе заряд q=40нКл, влетела в электрическое поле в на­правлении силовых линий. После прохождения разности потенциалов U = 200 В пылинка имела скорость u = 10 м/с. Определить скорость u₀ пылинки до того, как она влетела в поле.

42. Электрон, обладавший кинетической энергией T = 10 эВ, вле­тел в однородное электрическое поле в направлении силовых линий поля. Какой скоростью будет обладать электрон, пройдя в этом поле разность потен­циалов U= 8В?

43. Найти отношение скоростей ионов Сu⁺⁺ и К⁺, прошедших одинаковую разность потенциалов.

44. Электрон с энергией Т = 400 эВ (в бесконечнос­ти) движется вдоль силовой линии по направлению к поверхности металлической заряженной сферы радиусом R = 10 см. Определить минимальное рас­стояние а, на которое приблизится электрон к поверхности сферы, если заряд ее q = - 10 нКл.

45. Электрон, пройдя в плоском конденсаторе путь от одной пла­стины до другой, приобрел скорость u = 10⁵ м/с. Расстояние между пластинами d = 8 мм. Найти: 1) разность потенциалов U между пласти­нами; 2) поверхностную плотность зарядаs на пластинах.

46. Пылинка массой т = 5 нг, несущая на себе N = 10 электронов, прошла в вакууме ускоряющую разность потенциалов U = 1 MB. Ка­кова кинетическая энергия Т пылинки? Какую скорость u приобрела пылинка?

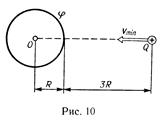
47. Какой минимальной скоростью u_min должен обладать протон, чтобы он мог достигнуть поверхности заряженного до потенциала j = 400 В металлического шара (рис.10)?

48. В однородное электрическое поле напряженностью Е = 200 В/м влетает (вдоль силовой линии) электрон со скоростью u₀=2 Мм/с. Определить расстояние l, которое пройдет электрон до точки, в которой его скорость будет равна половине начальной.

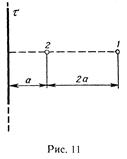
49. Электрическое поле создано бесконечной заряженной прямой линией с равномерно распределенным зарядом (t = 10 нКл/м). Опреде­лить кинетическую энергию Т₂ электрона в точке 2, если в точке1его кинетическая энергия T₁= 200эВ (рис.11).

50. Электрон движется вдоль силовой линии однородного элек­трического поля. В некоторой точке поля с потенциалом j₁ = 100 В электрон имел скорость 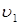= 6 Мм/с. Определить потенциал j₂ точки поля, дойдя до которой электрон потеряет половину своей ско­рости.

51. Конденсаторы емкостью C₁ = 5 мкФ и С₂ = 10 мкФ заряжены до напряжений U₁ = 60 В и U₂ = 100 В соответственно. Определить напряжение на обкладках конденсаторов после их соединения обклад­ками, имеющими одноименные заряды.

52. Конденсатор емкостью C₁ = 10 мкФ заряжен до напряжения U = 10 В. Определить заряд на обкладках этого конденсатора после того, как параллельно ему был подключен другой, незаряженный, конденса­тор ем­костью С₂ = 20 мкФ.

53. Конденсаторы емкостями C₁ = 2 мкФ, С₂ = 5 мкФ и С₃ = 10 мкФ соединены последовательно и находятся под напряжением U = 850 В. Определить на­пряжение и заряд на каждом из конденсато­ров.

54. Два конденсатора емкостями C₁ = 2 мкФ и С₂ = 5 мкФ заря­жены до напряжений U₁ = 100 В и U₂ = 150 В соответственно. Опреде­лить напряжение на обкладках конденсаторов после их соединения обкладками, имеющими разноименные заряды.

55. Два одинаковых плоских воздушных конденсато­ра емкостью С=100 пФ каждый соединены в батарею последовательно. Определить, на сколько изменится емкость С батареи, если пространство между пластинами одного из конденсаторов заполнить парафином.

56. Два конденсатора емкостями C₁ = 5 мкФ и С₂ = 8 мкФ соеди­нены последовательно и присоединены к батарее с ЭДС e = 80 В. Оп­ределить заряды q₁ и q₂ конденсаторов и разности потенциалов U₁ и U₂. между их обкладками.

57. Плоский конденсатор состоит из двух круглых пластин радиу­сом R = 10см каждая. Расстояние между пластинами d = 2 мм. Конден­сатор присоединен к источ­нику напряжения U = 80 В. Определить заряд q и на­пряженность Е поля конденсатора в двух случаях: а) ди­электрик — воздух; б) диэлектрик — стекло.

58. Два металлических шарика радиусами R₁ = 5 см и R₂ = 10 см имеют заряды q₁ = 40 нКл и q₂ = -20 нКл соответственно. Найти энер­гию W, которая выделится при разряде, если шары соединить проводни­ком.

59. Пространство между пластинами плоского конденсатора за­полнено двумя слоями диэлектрика: стекла толщиной d₁ = 0,2 см и слоем парафина толщиной d₂ = 0,3 см. Разность потенциалов между обкладками U = 300 В. Определить напряженность E поля и падение потенциала в каждом из слоев.

60. Плоский конденсатор с площадью пластин S = 200 см² каждая заряжен до разности потенциалов U =2 кВ. Расстояние между пласти­нами d=2 см. Диэлектрик – стекло. Определить энергию W поля кон­денсатора и плотность энергии w поля.

 

ПОСТОЯННЫЙ ЭЛЕКТРИЧЕСКИЙ ТОК

 

Сила постоянного тока

I = q/t,

где q – заряд, прошедший через поперечное сечение проводника за время t.

Плотности тока

j = I/S,

где S – площадь поперечного сечения проводника.

Связь плотности тока со средней скоростью <υ> направлен­ного движения заряженных частиц

j = qn<υ>,

где q – заряд частицы; n – концентрация заряженных частиц.

Закон Ома:

а) для участка цепи, не содержащего ЭДС, где φ₁ – φ₂ = U – разность потенциалов (напряжение) на концах участка цепи; R – сопротивление участка;

б) для участка цепи, содержащего ЭДС, где 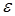– ЭДС источника тока; R – полное сопротивление участка (сумма внешних и внутренних сопротивлений);

в) 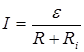для замкнутой (полной) цепи, где R – внеш­нее сопротивление цепи; R_i – внутреннее сопротивление цепи.

Законы Кирхгофа:

а) ∑ I_i = 0 – первый закон;

б) ∑ I_iR_i = ∑ – второй закон,

где ∑ I_i – алгебраическая сумма сил токов, сходящихся в узле; ∑ I_iR_i – алгебраическая сумма произведений сил токов на сопротивление уча­стков; ∑ e_i – алгебраическая сумма ЭДС.

Сопротивление R и проводимость G проводника

R = ρl/S, G=γS/l,

где ρ – удельное сопротивление; γ – удельная проводимость; l – длина проводника; S – площадь поперечного сечения проводника.

Сопротивление системы проводников:

а) R = ∑ R_i при последовательном соединении;

б) 1/R = ∑(1/R_i) при параллельном соединении, где R_i – сопро­тивление i-го проводника.

Работа тока

A = IUt, A = I²Rt, A = U²t/R.

Первая формула справедлива для любого участка цепи, на кон­цах которого поддерживается напряжение U, последние две – для уча­стка, не содержащего ЭДС.

Мощность тока

P = IU, P = I²R, P=U²/R.

Закон Джоуля – Ленца

Q = I²Rt.

Закон Ома в дифференциальной форме

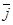= γ ,

где γ – удельная проводимость; – напряженность электрического поля; 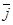– плотность тока.

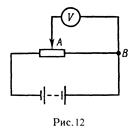Пример 1. Потенциометр сопротивлением R = 100 Ом под­ключен к батарее с ЭДС e = 150 В и внутренним сопротивлением R_i = 50 Ом. Определить: 1) показание вольтметра между сопротивлением R_v = 500 Ом, соеди­ненного с одной из клемм потенциометра и подвижным контактом, установленным посе­редине потенциометра; 2) разность потен­циалов между теми же точками потенцио­метра при отключении вольтметра.

 

Р е ш е н и е. 1. Показание вольт­метра, подключенного к точкам А и В (рис. 12), определим по формуле

U₁ = I₁R₁,

где R₁ – сопротивление параллельно соединенных вольтметра и поло­вины потенциометра; I₁ – суммарная сила тока в ветвях этого соедине­ния (она равна силе тока в неразветвленной части цепи).

Силу тока I₁ найдем по закону Ома для полной цепи:

I₁ = e /(R_e +R_i), (1)

где R_e – сопротивление внешней цепи. Это сопротивление есть сумма двух сопротивлений:

R_e = R/2 +R₁. (2)

Сопротивление R₁ найдем по формуле параллельного соедине­ния проводников 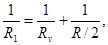откуда

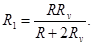
Подставив в (1) выражение R_e по (2), найдем

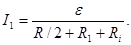
В данном случае решение задачи в общем виде было бы гро­моздким. Поэтому удобно вычисление величин провести раздельно:

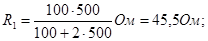
U₁ = 1,03·45·5 В = 46,9 В.

2. Разность потенциалов между точками А и В при отключен­ном вольтметре равна произведению силы тока I ₂ на половину сопро­тивления потенциометра:

U₂ = I₂ ·R/ 2, (3)

где I₂ – сила тока в цепи при отключенном вольтметре. Ее определим по формуле

I₂ = e /(R + R_i).

Подставив выражение I₂ в (3), найдем

U₂ = e / (R + R_i)·R/2.

Произведем вычисления:

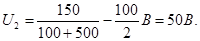
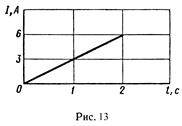Пример 2. Сила тока в проводнике сопротивлением R = 20 Ом нарастает в течение времени Δt = 2 с по линейному закону от I₀ = 0 до I = 6 А (рис 13). Определить теплоту Q ₁, выделившуюся в этом проводнике за первую секунду, и Q₂ – за вторую, а также найти отношение q₁/q₂.

 

 

Р е ш е н и е. Закон Джоуля – Ленца в виде Q = I²Rt справедлив для постоянного тока (I = const). Если же сила тока в проводнике изменяется, то указанный закон спра­ведлив для бесконечно малого интервала времени и записывается в виде

dQ = I²Rdt. (1)

Здесь сила тока I является некоторой функцией времени. В данном случае

I = kt, (2)

где k – коэффициент пропорциональности, характеризующий скорость изменения силы тока:

С учетом (2) формула (1) примет вид

dQ = k²Rt²dt. (3)

Для определения теплоты, выделившейся за конечный интер­вал времени Δ t, выражение (3) надо проинтегрировать в пределах от t ₁ до t ₂:

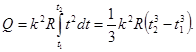
Произведем вычисления:

Q₁ = 1/3 · 3² · 20(1 – 0) Дж = 60 Дж;

Q₂ = 1/3 · 3² · 20(8 – 1) Дж = 420 Дж.

Следовательно,

Q₂ / Q₁ = 420 / 60 = 7,

т. е. за вторую секунду выделится теплоты в семь раз больше, чем за первую.

 

Пример 3. Пространство между пластинами плоского конден­сатора имеет объем V = 375 см³ и заполнено водородом, который час­тично ионизирован. Площадь пластин конденсатора S = 250 см². При каком напряжении U между пластинами конденсатора сила тока I, про­текающего через конденсатор, достигнет значения 2мкА, если концен­трация n ионов обоих знаков в газе равна 5,3 · 10⁷ см^–3. Принять под­вижность ионов b ₊= 5,4 · 10 ^–4 м² / (В · с), b _-=7,4 · 10^-4 м²/(В · с).

Р е ш е н и е. Напряжение U на пластинах конденсатора свя­зано с напряженностью Е электрического поля между пластинами и расстояни