по пакетам прикладных программ
Заляжко Анастасии, 413 группы.
Для изучения программы Gretl выбрали набор данных из библиотеки Ramanathan data7-12. Этот набор содержит данные о ценах и характеристиках американских 2-дверных седанов и хэтчбеков в 1995 году. Одно наблюдение - это одна машина и ее характеристики. Источник – подопечный автомобильный ежегодник. Набор содержит 82 наблюдения.
Опишем переменные:
1. price – цена автомобиля, 8395-68603 $;
2. hatch – принимает значения 1 для хэтчбека и 0 для седана;
3. wbase – колесная база, измеряется в дюймах, 93.1-113.8;
4. length – длина автомобиля в дюймах, 149.4-207;
5. width – ширина автомобиля в дюймах, 53.9-75.5;
6. height – высота автомобиля в дюймах, 46.3-55.2;
7. weight – масса автомобиля в сотнях фунтов, 18.08-38.18;
8. cyl – количество цилиндров, 3-8 цилиндров(штук);
9. liters – объем двигателя автомобиля в литрах, 1-2.3 литров;
10. gasmpg – мили на галлон газа, среднее количество между городом и шоссе(это тоже самое, что и литры на километр, 1 л/100 км = 235.2145833 mpg(миль/галлон))
11. trans – принимает значения 1 для автоматической коробки передач и 0 для механической.
Переменные hatch и trans - качественные.
С первого взгляда на данные можно сказать, что объем двигателя, количество цилиндров, тип коробки передач зависят от цены. Очевидно, что чем качественнее, лучше машина по каким-либо критериям, тем она дороже. Например, если объем двигателя увеличивается, то увеличивается и стоимость АМ. А вот высота автомобиля никак не зависит от длины, или высота АМ не зависит от типа коробки передач.
Выбрала этот набор данных, потому что у меня есть водительские права, я езжу на машине и более менее в них что-то понимаю.
Корреляционная матрица.
| price | wbase | liters | gasmpg | |
| 1,0000 | 0,1853 | 0,6397 | -0,5272 | price |
| 1,0000 | 0,2739 | -0,4133 | wbase | |
| 1,0000 | -0,6797 | liters | ||
| 1,0000 | gasmpg |
Мы выбираем переменные (регрессоры), которые имеют наибольший коэффициент корреляции. Регерессоры – X1=liters, X2=wbase, X3=gasmpg. Зависимая переменная Y=rice – стоимость автомобиля. Стоимость АМ зависит от объема двигателя, колесной базы и количества миль на галлон газа.
1. Тест Чоу – сравнение регрессионных моделей на двух выборках. Предлагается разбить выборку на две части. Тест проверяет гипотезу о совпадении линейной регрессионной модели для двух частей выборки. (85-86)
У нас имеется две регрессионные модели. Делим выборку на две (на хэтчбеки и седаны). (Выборка -> Изменить на основе критерия).
1) hatch=1
2) hatch=0
Сначала нужно посчитать три регрессии.
Модель 1: МНК, использованы наблюдения 1-82
Зависимая переменная: price
| Коэффициент | Ст. ошибка | t-стат. | P-значение | ||
| const | 22,4385 | 22,7234 | 0,9875 | 0,32647 | |
| wbase | -0,0728025 | 0,196864 | -0,3698 | 0,71253 | |
| liters | 3,82443 | 0,855977 | 4,4679 | 0,00003 | *** |
| gasmpg | -0,258217 | 0,171084 | -1,5093 | 0,13526 |
| Среднее зав. перемен | 18,15477 | Ст. откл. зав. перемен | 8,462857 | |
| Сумма кв. остатков | 3329,189 | Ст. ошибка модели | 6,533140 | |
| R-квадрат | 0,426122 | Испр. R-квадрат | 0,404050 | |
| F(3, 78) | 19,30581 | Р-значение (F) | 1,85e-09 | |
| Лог. правдоподобие | -268,2073 | Крит. Акаике | 544,4146 | |
| Крит. Шварца | 554,0415 | Крит. Хеннана-Куинна | 548,2797 |
Модель 2: МНК, использованы наблюдения 1-27 (hatch=1)
Зависимая переменная: price
| Коэффициент | Ст. ошибка | t-стат. | P-значение | |||
| const | 148,085 | 72,0849 | 2,0543 | 0,05148 | * | |
| wbase | -1,28623 | 0,68749 | -1,8709 | 0,07413 | * | |
| liters | 3,58619 | 1,45179 | 2,4702 | 0,02135 | ** | |
| gasmpg | -0,379178 | 0,275106 | -1,3783 | 0,18137 | ||
| Среднее зав. перемен | 18,40896 | Ст. откл. зав. перемен | 11,64201 | |
| Сумма кв. остатков | 1773,026 | Ст. ошибка модели | 8,779983 | |
| R-квадрат | 0,496864 | Испр. R-квадрат | 0,431237 | |
| F(3, 23) | 7,571088 | Р-значение (F) | 0,001073 | |
| Лог. правдоподобие | -94,80352 | Крит. Акаике | 197,6070 | |
| Крит. Шварца | 202,7904 | Крит. Хеннана-Куинна | 199,1483 |
Модель 3: МНК, использованы наблюдения 1-55 (hatch=0)
Зависимая переменная: price
| Коэффициент | Ст. ошибка | t-стат. | P-значение | ||
| const | -33,817 | 24,4716 | -1,3819 | 0,17303 | |
| wbase | 0,529791 | 0,216739 | 2,4444 | 0,01801 | ** |
| liters | 2,25759 | 1,16648 | 1,9354 | 0,05850 | * |
| gasmpg | -0,369085 | 0,246128 | -1,4996 | 0,13989 |
| Среднее зав. перемен | 18,02998 | Ст. откл. зав. перемен | 6,490258 | |
| Сумма кв. остатков | 1114,199 | Ст. ошибка модели | 4,674082 | |
| R-квадрат | 0,510170 | Испр. R-квадрат | 0,481357 | |
| F(3, 51) | 17,70594 | Р-значение (F) | 5,24e-08 | |
| Лог. правдоподобие | -160,7770 | Крит. Акаике | 329,5539 | |
| Крит. Шварца | 337,5833 | Крит. Хеннана-Куинна | 332,6589 |
Используем формулу для подсчета F-статистики:
Производя вычисления, получаем:
F(3, 76): площадь правее 5,044 = 0,00306067 (левее: 0,996939)
Значит, гипотеза о том, что регрессионные зависимости в обеих частях выборки совпадают, опровергается, так как площадь правее меньше 0.1. Значит мы не можем объединить две выборки в одну.
2. Длинная и короткая регрессии. (128-131)
Возникает вопрос о том, стоит ли добавлять/удалять некоторые переменные. (128-131). Необходимо выяснить, какая регрессия нам выгоднее.
Проверяем гипотезу о том, что короткая регрессия лучше длинной.
Сравниваем две модели:
Мы осуществим одну длинную регрессию и две коротких (на каждый Х соответственно).
Далее индекс u будет означать модель без ограничений, индекс r – с ограничением. Используем формулу:
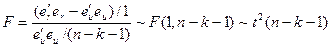
При длинной регрессии сумма квадратов остатков = 3426.418.
Сначала берём X1 = wbase. Осуществив регрессию, выпишем сумму квадратов остатков = 5601.928.
Получаем F = 49,5251 = t2 => t = 7.037 > 1, значит мы получили модель без ограничений. (y = Xβ+zγ+ε)
Далее берём X2 = liters. Осуществив регрессию, выпишем сумму квадратов остатков = 3427.060.
Получаем F = 0.6421 = t2 => t = 0.1208 < 1, значит мы получили модель с ограничением. (y = Xβ+ε)
Таким образом, мы получили, что первая короткая регрессия хуже длинной, а вторая короткая регрессия лучше длинной.
Модель 4: МНК, использованы наблюдения 1-82
Зависимая переменная: price
| Коэффициент | Ст. ошибка | t-стат. | P-значение | |||
| const | -21,7602 | 23,6783 | -0,9190 | 0,36086 | ||
| wbase | 0,387336 | 0,2296 | 1,6870 | 0,09550 | * | |
| Среднее зав. перемен | 18,15477 | Ст. откл. зав. перемен | 8,462857 | |
| Сумма кв. остатков | 5601,928 | Ст. ошибка модели | 8,368041 | |
| R-квадрат | 0,034353 | Испр. R-квадрат | 0,022282 | |
| F(1, 80) | 2,845989 | Р-значение (F) | 0,095498 | |
| Лог. правдоподобие | -289,5430 | Крит. Акаике | 583,0860 | |
| Крит. Шварца | 587,8994 | Крит. Хеннана-Куинна | 585,0185 |
Модель 5: МНК, использованы наблюдения 1-82
Зависимая переменная: price
| Коэффициент | Ст. ошибка | t-стат. | P-значение | ||
| const | 5,50166 | 1,84695 | 2,9788 | 0,00383 | *** |
| liters | 4,68211 | 0,62893 | 7,4446 | <0,00001 | *** |
| Среднее зав. перемен | 18,15477 | Ст. откл. зав. перемен | 8,462857 | |
| Сумма кв. остатков | 3427,060 | Ст. ошибка модели | 6,545094 | |
| R-квадрат | 0,409251 | Испр. R-квадрат | 0,401867 | |
| F(1, 80) | 55,42140 | Р-значение (F) | 9,81e-11 | |
| Лог. правдоподобие | -269,3953 | Крит. Акаике | 542,7905 | |
| Крит. Шварца | 547,6039 | Крит. Хеннана-Куинна | 544,7230 |
Модель 6: МНК, использованы наблюдения 1-82
Зависимая переменная: price
| Коэффициент | Ст. ошибка | t-стат. | P-значение | ||
| const | 3,20543 | 18,9657 | 0,1690 | 0,86622 | |
| liters | 4,66018 | 0,658004 | 7,0823 | <0,00001 | *** |
| wbase | 0,0228577 | 0,187884 | 0,1217 | 0,90348 |
| Среднее зав. перемен | 18,15477 | Ст. откл. зав. перемен | 8,462857 | |
| Сумма кв. остатков | 3426,418 | Ст. ошибка модели | 6,585771 | |
| R-квадрат | 0,409362 | Испр. R-квадрат | 0,394409 | |
| F(2, 79) | 27,37684 | Р-значение (F) | 9,27e-10 | |
| Лог. правдоподобие | -269,3876 | Крит. Акаике | 544,7751 | |
| Крит. Шварца | 551,9953 | Крит. Хеннана-Куинна | 547,6739 |
3. Сравнение параллельных (не являющихся вложенными) моделей.
К примеру, мы решили, что стоит ограничиваться не более, чем одной, но не ясно, какой, объясняющей переменной. Мы должны выяснить это. (132-133)
Основная гипотеза: y = β0 + x1 β1 + ε
Альтернативная гипотеза: y = β1 + x2 β2 + ε
Берём Х2 = wbase, делаем регрессию Y на X2 и сохраняем расчётное значение wbase1, далее делаем регрессию Y на X1 = liters и сохраняем значение как liters1. Выписываем из таблицы значения t-статистики напротив сохраненных переменных.
Модель 8: МНК, использованы наблюдения 1-82
Зависимая переменная: price
| Коэффициент | Ст. ошибка | t-стат. | P-значение | ||
| const | -2,27046 | 18,8373 | -0,1205 | 0,90437 | |
| wbase | 0,0228577 | 0,187884 | 0,1217 | 0,90348 | |
| liters1 | 0,995317 | 0,140536 | 7,0823 | <0,00001 | *** |
| Среднее зав. перемен | 18,15477 | Ст. откл. зав. перемен | 8,462857 | |
| Сумма кв. остатков | 3426,418 | Ст. ошибка модели | 6,585771 | |
| R-квадрат | 0,409362 | Испр. R-квадрат | 0,394409 | |
| F(2, 79) | 27,37684 | Р-значение (F) | 9,27e-10 | |
| Лог. правдоподобие | -269,3876 | Крит. Акаике | 544,7751 | |
| Крит. Шварца | 551,9953 | Крит. Хеннана-Куинна | 547,6739 |
Модель 7: МНК, использованы наблюдения 1-82
Зависимая переменная: price
| Коэффициент | Ст. ошибка | t-стат. | P-значение | ||
| const | 4,48956 | 8,52426 | 0,5267 | 0,59989 | |
| liters | 4,66018 | 0,658004 | 7,0823 | <0,00001 | *** |
| wbase1 | 0,0590124 | 0,485067 | 0,1217 | 0,90348 |
| Среднее зав. перемен | 18,15477 | Ст. откл. зав. перемен | 8,462857 | |
| Сумма кв. остатков | 3426,418 | Ст. ошибка модели | 6,585771 | |
| R-квадрат | 0,409362 | Испр. R-квадрат | 0,394409 | |
| F(2, 79) | 27,37684 | Р-значение (F) | 9,27e-10 | |
| Лог. правдоподобие | -269,3876 | Крит. Акаике | 544,7751 | |
| Крит. Шварца | 551,9953 | Крит. Хеннана-Куинна | 547,6739 |
t (price, liters1, wbase)=7.0823
t (price, wbase1, liters)=0.1217
Далее считаем в разделе p-значений нормальное распределение:
Стандартное нормальное распределение:
площадь правее 7,0823 = 7,08907e-013
(двухстороннее значение = 1,41781e-012; дополняющее = 1)
S=7.08907e-013, S*=1-S, S*=1-7.08907e-013=0.9999999999993
Двухсторонне значение: 2S*=1.9999999999986
Стандартное нормальное распределение: площадь правее 0,1217 = 0,451568
(двухстороннее значение = 0,903137; дополняющее = 0,0968634)
S=0.451668, S*=0.548432
Двухсторонне значение: 2S*=1.096864
Оба значения > 0.5, следовательно, в обоих случаях гипотеза отвергнута быть не может. В обоих случаях получили наилучшую модель.
4. Тест на функциональную форму. (133-134)
Проверяем гипотезу о том, что квадраты добавлять не надо. Если гипотеза отвергается, то проверяем, нужно ли добавлять кубы.
Строим регрессию Y на Х1 и Х2, сохраняем расчётное значение qw1 и выписываем сумму квадратов остатков ESSR = 3426.418. Строим переменную, являющуюся квадратом значений qw1, делаем регрессию уже на оба икса и на квадрат значений qw1, выписываем сумму квадратов остатков ESSUR = 3401.207.
Модель 9: МНК, использованы наблюдения 1-82
Зависимая переменная: price
| Коэффициент | Ст. ошибка | t-стат. | P-значение | ||
| const | 3,20543 | 18,9657 | 0,1690 | 0,86622 | |
| wbase | 0,0228577 | 0,187884 | 0,1217 | 0,90348 | |
| liters | 4,66018 | 0,658004 | 7,0823 | <0,00001 | *** |
| Среднее зав. Перемен | 18,15477 | Ст. откл. зав. перемен | 8,462857 | |
| Сумма кв. остатков | 3426,418 | Ст. ошибка модели | 6,585771 | |
| R-квадрат | 0,409362 | Испр. R-квадрат | 0,394409 | |
| F(2, 79) | 27,37684 | Р-значение (F) | 9,27e-10 | |
| Лог. Правдоподобие | -269,3876 | Крит. Акаике | 544,7751 | |
| Крит. Шварца | 551,9953 | Крит. Хеннана-Куинна | 547,6739 |
Модель 10: МНК, использованы наблюдения 1-82
Зависимая переменная: price
| Коэффициент | Ст. ошибка | t-стат. | P-значение | ||
| const | -3,21477 | 20,8067 | -0,1545 | 0,87761 | |
| wbase | 0,129365 | 0,234755 | 0,5511 | 0,58316 | |
| liters | -0,101361 | 6,29669 | -0,0161 | 0,98720 | |
| sq_qw1 | 0,0231829 | 0,0304884 | 0,7604 | 0,44932 |
| Среднее зав. Перемен | 18,15477 | Ст. откл. зав. перемен | 8,462857 | |
| Сумма кв. остатков | 3401,207 | Ст. ошибка модели | 6,603424 | |
| R-квадрат | 0,413708 | Испр. R-квадрат | 0,391158 | |
| F(3, 78) | 18,34650 | Р-значение (F) | 4,21e-09 | |
| Лог. Правдоподобие | -269,0848 | Крит. Акаике | 546,1696 | |
| Крит. Шварца | 555,7964 | Крит. Хеннана-Куинна | 550,0346 |
Используем формулу:
(для квадратов)
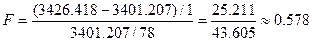
Подставляем в распределение Фишера, получаем:
F(1, 78): площадь правее 0,578 = 0,449389 (левее: 0,550611)
То есть гипотеза не отвергается и квадраты добавлять не нужно.
Проверим, надо ли добавлять кубы.
Теперь k=3+2=5.
Строим регрессию Y на Х1 и Х2, сохраняем расчётное значение qw1 и выписываем сумму квадратов остатков ESSR = 3426.418. Строим переменную, являющуюся кубом значений qw1, делаем регрессию уже на оба икса и на куб значений qw1, выписываем сумму квадратов остатков ESSUR = 3395.068.
Модель 10: МНК, использованы наблюдения 1-82
Зависимая переменная: price
| Коэффициент | Ст. ошибка | t-стат. | P-значение | ||
| const | -5,55983 | 21,9271 | -0,2536 | 0,80050 | |
| wbase | 0,151296 | 0,247209 | 0,6120 | 0,54231 | |
| liters | 1,89618 | 3,50921 | 0,5403 | 0,59050 | |
| cub | 0,000386958 | 0,000482534 | 0,8019 | 0,42503 |
| Среднее зав. перемен | 18,15477 | Ст. откл. зав. перемен | 8,462857 | |
| Сумма кв. остатков | 3395,068 | Ст. ошибка модели | 6,600699 | |
| R-квадрат | 0,414192 | Испр. R-квадрат | 0,391661 | |
| F(3, 78) | 18,38314 | Р-значение (F) | 4,08e-09 | |
| Лог. правдоподобие | -269,0509 | Крит. Акаике | 546,1018 | |
| Крит. Шварца | 555,7287 | Крит. Хеннана-Куинна | 549,9669 |
В распределение Фишера подставляем:
F(1, 77): площадь правее 0,711 = 0,401724 (левее: 0,598276)
Подтвердили наш результат. Кубы добавлять не нужно.
5. Процедура пошагового отбора переменных. (122-124)
Первый шаг не выполняем, так как число регрессоров у нас больше двух.
Заходим в критические значения, распределение Фишера, считаем:
F(1; 79; 0.05) = 0.823641 = 
F(1; 79; 0.95) = 0.332694 = 
.
Мы обозначили большее число , а меньшее обозначили .
Далее мы считаем коэффициент корреляции между Y и X1 и между Y и X2. Итак,
corr(price, liters) = 0,63972761; corr(price, wbase) = 0,18534501.
Выберем тот Х, у которого с нашим Y коэффициент корреляции больше, то есть берём Х = liters. Мы хотим выяснить, стоит ли добавлять переменную price.
Для этого считаем
ESSR = 3427.060 ESSUR = 3426.418 => F = 0.0418
F < Fискл < Fвкл – так как имеет место такое соотношение, то регрессор liters не может быть включен в список регрессоров. Второй шаг нет смысла повторять, так как список регрессоров не изменился.
6. Коррекция на гетероскедастичность. (168-181)
Проверяем гипотезу о том, что гетероскедастичности нет, то есть все дисперсии равны σ12 = … = σn2.
Тест Уайта.
Считаем регрессию Y на оба наших икса и сохраняем квадрат остатков еt2 – и теперь уже считаем регрессию квадрата остатков на X1, X2, X1*X2, X12, X22, const.
Модель 11: МНК, использованы наблюдения 1-82
Зависимая переменная: price
| Коэффициент | Ст. ошибка | t-стат. | P-значение | ||
| const | 1117,32 | 368,247 | 3,0342 | 0,00330 | *** |
| wbase | -23,1138 | 7,44895 | -3,1030 | 0,00269 | *** |
| liters | 59,1081 | 20,631 | 2,8650 | 0,00539 | *** |
| sq_wbase | 0,119757 | 0,0376092 | 3,1843 | 0,00210 | *** |
| sq_liters | -0,126857 | 0,672135 | -0,1887 | 0,85080 | |
| prouzv | -0,534791 | 0,192421 | -2,7793 | 0,00686 | *** |
| Среднее зав. перемен | 18,15477 | Ст. откл. зав. перемен | 8,462857 | |
| Сумма кв. остатков | 2976,042 | Ст. ошибка модели | 6,257671 | |
| R-квадрат | 0,486997 | Испр. R-квадрат | 0,453247 | |
| F(5, 76) | 14,42945 | Р-значение (F) | 6,32e-10 | |
| Лог. правдоподобие | -263,6098 | Крит. Акаике | 539,2196 | |
| Крит. Шварца | 553,6599 | Крит. Хеннана-Куинна | 545,0172 |
Коэффициент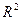 
=0.453247. Умножаем его на 2 и получаем:
0.453247*2=37.166254.
И подставляем это значение в Хи-квадрат с 5 степенями свободы:
Хи-квадрат(5): площадь правее 37,1663 = 5,54696e-007 (левее: 0,999999)
Это очень маленькое число. Значит гипотезу о равенстве дисперсий отвергаем, то есть гетероскедастичность есть.
Теперь сделаем другой тест.
Тест Голфелда-Куандта.
Берем переменную wbase и сортируем данные по убыванию.
Мы должны исключить d средних наблюдений из середины.
.
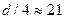Получили два интервала [0,32] и [63,82]. Изменяем выборку на основе критерия wbase<102.8||wbase>103.4. Для наблюдений 1-31 находим сумма квадратов остатков 
. Для наблюдений 63-82 получаем: 
. Считаем:
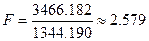. Подставляем полученное значение в распределение Фишера:
F(29, 29): площадь правее 2,579 = 0,00648823 (левее: 0,993512)
Таким образом принимаем гипотезу о равенстве дисперсий – гетероскедастичности в случае переменной wbase нет.
Теперь проведем аналогичные рассуждения для переменной liters.
[0,33], [60,82] – интервалы для этой переменной.
, 
.
. Подставляем в распределение Фишера со степенями свободы:
82/2-22/2=28
F(28, 28): площадь правее 0,1317 =~ 1 (левее: 3,77973e-007)
В данном случае наша гипотеза отвергается, то есть дисперсии не равны между собой и гетероскедастичность есть в случае переменной liters.