Содержание
1. Введение в анализ и дифференциальное исчисление функции одного переменного
2. Дифференциальное исчисление функций и его приложение
3. Интегральное исчисление функции одного переменного
Введение в анализ и дифференциальное исчисление функции одного переменного
1. Вычислить предел: 
.
Решение.
При 
имеем
Следовательно,
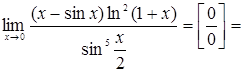
2. Найти асимптоты функции: 
.
Решение.
Очевидно, что функция не определена при 
.
Отсюда получаем, что
Следовательно, 
– вертикальная асимптота.
Теперь найдем наклонные асимптоты.
Следовательно, 
– наклонная асимптота при 
.
3. Определить глобальные экстремумы: 
при 
.
Решение.
Известно, что глобальные экстремумы функции на отрезке достигаются или в критических точках, принадлежащих отрезку, или на концах отрезка. Поэтому сначала находим 
.
.
А затем находим критические точки.
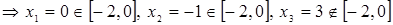
Теперь найдем значение функции на концах отрезка.
.
Сравниваем значения и получаем:
4. Исследовать на монотонность, найти локальные экстремумы и построить эскиз графика функции: 
.
Решение.
Сначала находим .
.
Затем находим критические точки.
| x |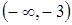 
| –3 | 
| 
| |
|
| – | + | + | ||
| убывает | min | возрастает | возрастает | возрастает |
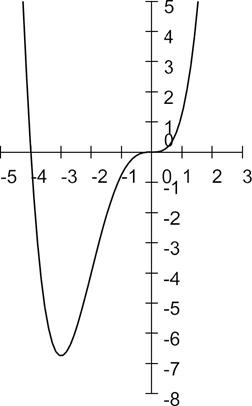
Отсюда следует, что функция
возрастает при 
,
убывает при 
.
Точка 
– локальный минимум.
5. Найти промежутки выпуклости и точки перегиба функции: 
.
Решение
Чтобы найти промежутки выпуклости и точки перегиба, найдем вторую производную функции.
.
.
.
| x | 
| –2 |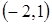 
| 
| |
| – | – | + | ||
| вогнутая | перегиб | выпуклая | перегиб | вогнутая |
Отсюда следует, что функция
выпуклая при 
,
вогнутая при 
.
Точки 
, 
– точки перегиба.
Дифференциальное исчисление функций и его приложение»
1. Провести полное исследование свойств и построить эскиз графика функции 
.
Решение.
1) Область определения функции
.
2) Функция не является четной или нечетной, так как
.
3) Теперь найдем точки пересечения с осями:
а) с оx: 
, б) с oy .
4) Теперь найдем асимптоты.
а)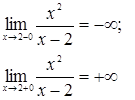 
А значит, 
является вертикальной асимптотой.
б) Теперь найдем наклонные асимптоты
Отсюда следует, что
является наклонной асимптотой при 
.
5) Теперь найдем критические точки
не существует при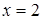 
.
6) 
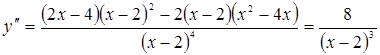
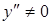
не существует при
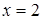
| x |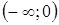 
| 
| 
| 
| |||
| + | – | Не сущ. | – | + | ||
|
| – | – | – | Не сущ. | + | + | + |
| y | возрастает выпуклая | max
| убывает выпуклая | не сущ. | убывает вогнутая | min
| возрастает вогнутая |
Построим эскиз графика функции 
2. Найти локальные экстремумы функции 
.
Решение.
Сначала найдем частные производные
Известно, что необходимым условием существования экстремума является равенство нулю частных производных.
То есть мы получили одну критическую точку: 
. Исследуем ее.
Далее проведем исследование этой точки.
Для чего найдем предварительно частные производные второго порядка
Для точки 
:
.
Следовательно, точка 
не является точкой экстремума.
Это означает, что точек экстремума у функции
нет.
3. Определить экстремумы функции 
, если 
.
Решение.
Сначала запишем функцию Лагранжа
.
И исследуем ее
(Учитываем, что по условию 
)
То есть мы получили четыре критические точки.
В силу условия 
нам подходит только первая 
.
Исследуем эту точку.
Вычислим частные производные второго порядка:
Отсюда получаем, что
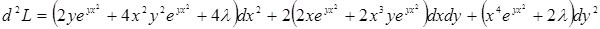
Теперь продифференцируем уравнение связи
.
Для точки
Далее получаем
То есть мы получили отрицательно определенную квадратичную форму.
Следовательно,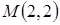 
– точка условного локального максимума.
.