ОБРАБОТКА И АНАЛИЗ РЕЗУЛЬТАТОВ ЛАБОРАТОРНОГО ФИЗИЧЕСКОГО ЭКСПЕРИМЕНТА
МЕТОДИЧЕСКИЕ УКАЗАНИЯ ДЛЯ СТУДЕНТОВ ВСЕХ НАПРАВЛЕНИЙ ПОДГОТОВКИ ВСЕХ ФОРМ ОБУЧЕНИЯ
Составители:
Л. А. Буркова
К. О. Урюпина
Министерство образования и науки Российской Федерации
ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ
«САНКТ-ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ
ТЕХНОЛОГИИ И ДИЗАЙНА»
ОБРАБОТКА И АНАЛИЗ РЕЗУЛЬТАТОВ ЛАБОРАТОРНОГО ФИЗИЧЕСКОГО ЭКСПЕРИМЕНТА
МЕТОДИЧЕСКИЕ УКАЗАНИЯ ДЛЯ СТУДЕНТОВ ВСЕХ НАПРАВЛЕНИЙ ПОДГОТОВКИ ВСЕХ ФОРМ ОБУЧЕНИЯ
Составители:
Л. А. Буркова
К. О. Урюпина
Санкт-Петербург
Утверждено
на заседании кафедры физики
16.05.2013 г, протокол № 5
Рецензент
С. Ю. Иванова
Оригинал-макет подготовлен составителями и издан в авторской редакции
Подписано в печать 2.10.13. Формат 60х84 1/16, Печать трафаретная.
Усл. печ. л. 1.7. Тираж 100 экз. Заказ
Сайт: https://www.sutd.ru E-mail: phisicsutd@mail.ru
Отпечатано в типографии ФГБОУВПО «СПГУТД»
191028, Санкт-Петербург, ул. Моховая, 26
ВВЕДЕНИЕ
«Все люди по своей природе жаждут знать»
(Изречение на воротах ликейской Академии Аристотеля)
Знать – это значит измерить.
Иоганн Кеплер
Основная задача всякого физического эксперимента, в том числе и лабораторного, состоит в измерении физических величин. При этом измерением физической величины называется ее сравнение с однородной величиной, условно выбранной за единицу измерения. В результате измерения получают числовое значение измеряемой величины.
Абсолютно точных измерений не существует. Всякое измерение выполняется с некоторой погрешностью. Более того, многократно измеряя любую физическую величину, можно, вообще говоря, получить какие угодно результаты. Например, измеряя длину некоторого тела, получили следующий ряд результатов: l = 12,1; 11,9; 11,8; 12,2; 12,0; 12,1; 11,8; 12,1 мм, а также 12,2 мкм и 11,9 м. Результаты последних двух наблюдений в этом ряду могут быть и ошибочными, например, являться следствием небрежной записи. Их наличие, однако, подчеркивает, что принципиально и результат измерения, и его погрешность могут быть любыми, и, следовательно, оценивать точность измерения указанием результата и его погрешности неверно – они могут быть любыми (от -∞ до +∞).
Вместе с тем из анализа приведенного ряда результатов видно, что большие по величине погрешности (которыми, очевидно, отвечают оба последних результата) маловероятны. Таким образом, следует заключить, что для правильной характеристики результата измерений необходимо указать сам результат, значение его погрешности и соответствующее ей значение вероятности.
На практике результат измерения принято характеризовать тремя числами: значением среднего результата измерений, значением погрешности и значением вероятности того, что погрешность не выходит за указанные рамки. Погрешность и вероятность в этом случае, вообще говоря, называют доверительными. В дальнейшем для краткости мы будем называть их просто погрешностями и вероятностями.
Из сказанного следует, что значения погрешностей и вероятностей однозначно связаны друг с другом, а именно: чем больше погрешность, тем больше и вероятность того, что результат измерения находится в указанных пределах и наоборот. Это позволяет при обработке экспериментальных данных поступать двояко:
1. Можно произвольно задать значение погрешности и вычислить соответствующее ей значение вероятности.
2. Можно произвольно задать значение вероятности
3. (0 ≤ P ≤ 1) и вычислить соответствующие границы погрешности.
В студенческом лабораторном практикуме чаще используется второй способ. Разумно, однако, и значение вероятности выбирать, исходя из результатов измерений. Так, если результаты отдельных измерений относительно мало отличаются друг от друга, логично вероятность взять относительно большой и наоборот. Один из способов такого выбора вероятности рекомендуется ниже (раздел «Прямые и многократные измерения»).
Таким образом, при выполнении и характеристике результатов измерений следует придерживаться следующих правил:
1. Всякое измерение, по-возможности, должно быть проверено путем его многократного повторения.
2. При измерении может быть получен лишь приближенный результат.
3. Степень приближенности результата задается величиной (границей) погрешности.
4. Степень доверия к найденным границам погрешности выражается указанием их вероятности.
ПРЯМЫЕ МНОГОКРАТНЫЕ ИЗМЕРЕНИЯ
Прямыми называют такие измерения, в которых результат находят непосредственным отсчетом по шкале прибора. Примеры: измерение температуры термометром, давления – барометром, силы тока – амперметром, длины – линейкой или штангенциркулем, времени – секундомером и т.п.
Многократно прямые измерения производят в тех случаях, когда при повторных измерениях одной и той же физической величины тождественных условиях значения отсчетов не повторяются (например, из-за влияния различных случайных и трудноучитываемых обстоятельств). Кстати сказать, если разброс результатов при этом относительно мал (2-3 наименьших деления шкалы прибора), то это свидетельствует о правильном выборе прибора, о достаточной, но не чрезмерной его чувствительности.
Выполнение и обработку результатов прямых многократных измерений рекомендуется производить в следующем порядке:
1. Прямыми измерениями получить ряд значений 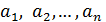
измеряемой величины.
2. Вычислить среднеарифметическое значение результата измерений (предварительный результат)
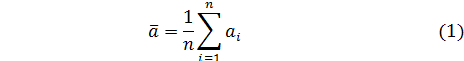
3. Вычислить отклонения отдельных результатов наблюдений от среднего
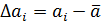 (2)
(2)
4. Вычислить значения 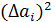 и их сумму
и их сумму 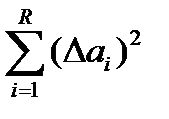
5. По формуле
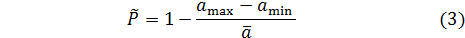
найти предварительное (оценочное) значение вероятности 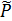 . Окончательное значение вероятности Р найти по нижеприведенной табл.1 как ближайшее к оценочному значению
. Окончательное значение вероятности Р найти по нижеприведенной табл.1 как ближайшее к оценочному значению 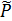 .
.
6. Для данных значений n и P найти по табл.1 коэффициент Стьюдента tnp и вычислить погрешность
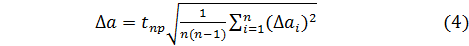
7. Округлив погрешность и предварительный результат, записать окончательный результат измерений
а = а ± ∆ а, P = α (5)
При этом коэффициент Стьюдента, зависящий от числа измерений n и выбранного значения вероятности P, вводится в связи с практической конечностью числа измерений. Значения коэффициентов Стьюдента приведено в табл.1.
Таблица 1.
Коэффициенты Стьюдента
| n | P | |||||
| 0,68 | 0,8 | 0,9 | 0,95 | 0,98 | 0,99 | |
| 2,0 | 3,1 | 6,3 | 12,7 | 31,8 | 63,7 | |
| 1,6 | 1,9 | 2,9 | 4,3 | 7,0 | 9,9 | |
| 1,3 | 1,6 | 2,4 | 3,2 | 4,5 | 5,8 | |
| 1,2 | 1,5 | 2,1 | 2,8 | 3,7 | 4,6 | |
| 1,2 | 1,5 | 2,0 | 2,6 | 3,4 | 4,3 | |
| 1,1 | 1,4 | 1,9 | 2,4 | 3,1 | 4,0 | |
| 1,1 | 1,4 | 1,9 | 2,4 | 3,0 | 3,7 | |
| 1,1 | 1,4 | 1,9 | 2,3 | 2,9 | 3,4 |
Выполнение указанных формулами (1)-(5) операций достаточно для исчерпывающей характеристики результата прямых многокрытных измерений. Ниже приведен пример компактного и удобного для обработки способа оформления результата прямых многократных измерений.
Пример.
Прямыми измерениями штангенциркулем диаметра Д некоторого вала получены его значения Дi, занесенные во 2-й столбец табл. 2.
Таблица 2.
Результат измерений диаметра вала
| n | Дi , мм | Δ Дi , мм | (Δ Дi ) 2, мм2 |
| 36,7 | 0,2 | 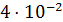
| |
| 36,2 | -0,3 | 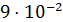
| |
| 36,8 | 0,3 | 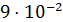
| |
| 36,5 | – | – | |
| 36,3 | -0,2 | 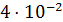
| |
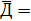 36,5 мм 36,5 мм
| 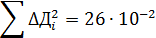
|
Под чертой внизу 2-го столба табл. 2 указано среднее значение диаметра вала 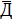 (предварительный результат измерений), а внизу 4-го столбца приведено значение суммы
(предварительный результат измерений), а внизу 4-го столбца приведено значение суммы 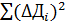 . Такое оформление результатов измерений компактно и удобно для дальнейшей обработки.
. Такое оформление результатов измерений компактно и удобно для дальнейшей обработки.
По формуле (3) оцениваем и находим вероятность P
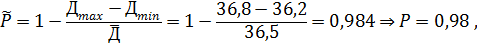
где Дmax и Дmin – соответственно максимальный и минимальный
диаметры из числа найденных значений Дi..
По табл. 1 определяем коэффициент Стьюдента t5; 0,98 =3,7 и вычисляем погрешность 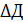
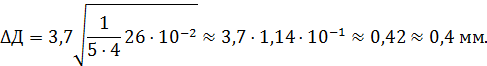
Окончательный результат измерений тогда
Д = (36,5 ± 0,4) мм, P =0,98.
ПРЯМЫЕ ОДНОКРАТНЫЕ ИЗМЕРЕНИЯ
Однократными измерениями ограничиваются тогда, когда при повторных наблюдениях получают одинаковые отсчеты и дальнейшее их повторение лишено смысла. Вообще говоря, это означает, что выбранный прибор для данных измерений слишком груб. Иногда однократным измерением приходится ограничиваться и по условиям измерений, например, из-за невозможности обеспечить тождественность их проведения. К примеру, определить координаты спутника Земли а данное время можно только один раз.
Погрешность прямого однократного измерения зависит от того, каким прибором или инструментом оно выполняется.
У многих, особенно электроизмерительных, приборов на их лицевых приборах указывается так называемый класс точности
| К |
| К |
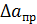 , а именно
, а именно
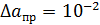
| К |
Пример
Верхний предел измерения вольтметра U max = 300 В, класс точности
| К |
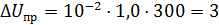 В.
В.
Это значение погрешности неизменно при любом отсчете, взятом со шкалы данного прибора.
Вероятность погрешностей, определяемых по формуле (6), полагается равной единице (Р = 1). Если же необходимо (см. раздел «Косвенные измерения») вычислить погрешность 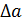 , определенную с вероятностью 0 ≤ P ≤ 1, то
, определенную с вероятностью 0 ≤ P ≤ 1, то
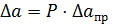 . (7)
. (7)
Пример
Ток в цепи измеряется амперметром, верхний предел измерения которого Imax = 2 A, а класс точности
| К |
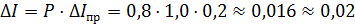 A.
A.
Окончательный результат данного однократного прямого измерения силы тока записывается в виде
I= (0,58 ± 0,02) A, P= 0,8.
На электросопротивлениях и емкостях предельные погрешности обычно указываются в процентах к их номиналу. Например, запись на электросопротивлении
R =1кОм±10%
означает, что предельная погрешность данного сопротивления в 1 кОм с вероятностью P =1 составляет значение
Δ Rпр = 0,1∙1=0,1 кОм, P =1.
В табл.3 указаны предельные погрешности приборов и инструментов, наиболее употребляемых в студенческом лабораторном физическом практикуме.
Таблица 3.
Погрешности лабораторных приборов и инструментов
| Прибор или инструмент | Цена деления прибора | Предельная погрешность при P =1 | |
| Измерительная линейка | 1 мм/дел | 1 мм | |
| 1 см/дел | 0,5 см | ||
| Штангенциркуль | 0,1 мм/дел | 0,1 мм | |
| 0,05 мм/дел | 0,05 мм | ||
| Микрометр | 0,01 мм/дел | 0,01 мм | |
| Микроскоп | Δ b мм/дел | Δ b мм | |
| Весы технические до 2 кг | 1 г | ||
| Весы аналитические до 200 г | 0,1 мг/дел | 1 мг | |
| Секундомер | 0,1 с/дел | 0,3 с | |
| 0,2 с/дел | 0,4 с | ||
| 0,05 с/дел | 0,3 с | ||
| Часы с секундной стрелкой | 1 с/дел | 1 с | |
| Термометр | 1°C/дел | 1°C | |
| 2°C/дел | 2°C | ||
| Барометр | Δ h мм рт. ст./дел | Δ h мм рт. ст. | |
| Δ p Па/дел | Δ p Па | ||
| Прибор с указанным классом точности К | С | 10-2 ∙
| |
| Электроизмерительный прибор без класса точности | С | С∙1дел | |
| Магазин, мост без класса точности и без паспортных данных | С | ± 5% от измеренного значения | |
| Табличная величина | ± 0,5 единицы последнего приведенного в ее записи разряда |
Погрешности, указанные в табл. 3, включают в себя неточности изготовления приборов, погрешности в нанесении их шкал, а также погрешности счета показаний (округление отчетов), которые поэтому отдельно не рассматриваются.
Погрешности табл. 3 являются предельными, т.е. отвечают вероятности P =1. Для перехода к погрешностям Δ a, заданным с вероятностями
0 ≤ P ≤ 1, следует воспользоваться выражением (7), согласно которому 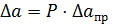 .
.
Обобщая правила вычисления погрешностей в прямых измерениях необходимо сделать следующее замечание. При прямых измерениях каким-либо прибором, когда получаются неповторяющиеся отсчеты и нужно находить среднее, прежде всего, следует оценить приборную погрешность 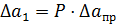 . Если вычисленная по формуле (4) погрешность среднего
. Если вычисленная по формуле (4) погрешность среднего 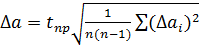 окажется по крайней мере в 1,5-2 раза меньше, чем приборная Δ a 1, то погрешностью среднего Δ a 2 пренебрегают. Действительно, погрешность среднего Δ a 2 можно сделать сколь угодно малой (например, за счет увеличения числа измерений n), однако измерения не могут быть точнее, чем это допускает прибор (его погрешность Δ a 1). И наоборот, когда погрешность среднего Δ a 2 больше приборной (в 1,5-2 раза), то пренебрегают последней. В редких случаях приблизительного равенства погрешностей Δ a 1 и Δ a 2 общую погрешность результата измерений вычисляют по формуле
окажется по крайней мере в 1,5-2 раза меньше, чем приборная Δ a 1, то погрешностью среднего Δ a 2 пренебрегают. Действительно, погрешность среднего Δ a 2 можно сделать сколь угодно малой (например, за счет увеличения числа измерений n), однако измерения не могут быть точнее, чем это допускает прибор (его погрешность Δ a 1). И наоборот, когда погрешность среднего Δ a 2 больше приборной (в 1,5-2 раза), то пренебрегают последней. В редких случаях приблизительного равенства погрешностей Δ a 1 и Δ a 2 общую погрешность результата измерений вычисляют по формуле
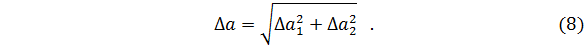
Вообще, если при измерениях величины a имеются независимые погрешности Δ a 1, Δ a 2, Δ a 3,… ее измерения, то общая погрешность определяется аналогично выражению (8)
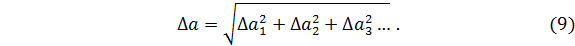
КОСВЕННЫЕ ИЗМЕРЕНИЯ
Во многих экспериментах интересующая нас величина сама непосредственно не измеряется. Вместо этого измеряются другие величины (аргументы a, b, и т.д.), а затем искомая величина Z (функция) вычисляется на основе известной функциональной зависимости
Z=Z(a, b, c, …). (10)
Такие измерения называются косвенными. Например, измеряя длину l, ширину b и высоту h прямоугольного параллелепипеда, можно затем по формуле V=lbh вычислить его объем V.
Конечное измерение  функции Z=Z(a, b, c, …), обусловленное изменением ее аргументов a, b, c, … на значения Δ a, Δ b, Δ c, … может быть вычислено по формуле
функции Z=Z(a, b, c, …), обусловленное изменением ее аргументов a, b, c, … на значения Δ a, Δ b, Δ c, … может быть вычислено по формуле
s w:val="28"/><w:lang w:val="EN-US"/></w:rPr><m:t>�c+…, (11)</m:t></m:r></m:oMath></m:oMathPara></w:p><w:sectPr wsp:rsidR="00000000" wsp:rsidRPr="00134194"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></wx:sect></w:body></w:wordDocument>"> 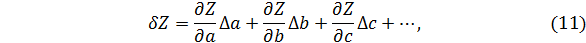
где 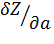 ,
, 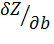 ,
, 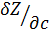 ,… - частные производные функции Z по ее соответствующим аргументам.
,… - частные производные функции Z по ее соответствующим аргументам.
Рассматривая в выражении (11) величины Δ a, Δ b, Δ c, … как погрешности прямых (одно- или многократных) измерений аргументов a, b, c,…, мы можем сосчитать каждый член правой части формулы (11) вкладом в общую погрешность измерения функции Z. Полагая эти вклады независимыми, по аналогии с выражением (9) получаем общую формулу для вычисления погрешности Δ Z в косвенных измерениях
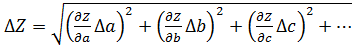 (12)
(12)
При вычислениях погрешности по формуле (12) также допустимо пренебрегать всеми членами подкоренного выражения, которые в 1,5-2 раза меньше максимального. Это существенно упрощает расчет погрешности, а также четко выявляет тот аргумент, погрешность которого имеет определяющее значение. Это важно знать для поиска путей повышения точности эксперимента, а также для обсуждения результатов.
Когда искомая функция Z = Z(a, b, c, …) удобна для логарифмирования (содержит много простых сомножителей), учитывают, что конечное изменение функции δ(lnZ) равно
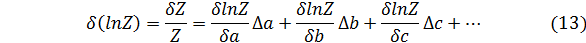
и на этой основе вместо выражения (12) получают следующне соотношение:

При этом значение квадратного корня в правой части (14) дает значение относительной погрешности 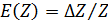 результата данного косвенного измерения.
результата данного косвенного измерения.
Пример
Формула для вычисления погрешности объема прямоугольного параллелепипеда V=lbh (l – длина, b – ширина, h – высота) по выражению (12)
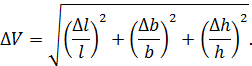
Очевидно, что вычисление погрешности Δ V по последнему выражению проще и допускает измерение параметров l, b и h в разных единицах.
Иногда в выражения (12) и (14) приходится подставлять погрешности Δ a, Δ b, Δ c, …, найденные с различными вероятностями P. Тогда общую вероятность результата косвенных измерений полагают равной наименьшей из использованных вероятностей прямых измерений аргументов (P = Pmin) и с большей уверенностью считают, что результирующая вероятность не ниже, чем P = Pmin.
Окончательно рекомендуется следующий порядок (алгоритм) обработки результатов в косвенных измерениях:
1. Выполнить (одно- или многократно) прямые измерения аргументов a, b, c, … измеряемой функции Z=Z(a, b, c, …) 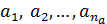 ;
; 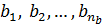 ;
; 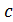 ;....
;....
2. Найти среднее значение аргументов
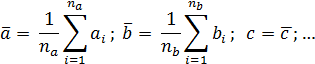
3. Вычислить значения
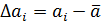 ;
; 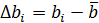 ; …
; … 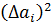 ;
; 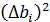 ;…
;… 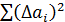 ;
; 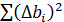 ;…
;…
4. Вычислить оценочные значения вероятностей
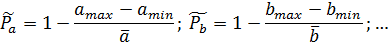
За общую вероятность результата косвенного измерения взять ближайшее к минимальному оценочному значение вероятности из табл. 1. (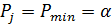 ).
).
5. Определить по табл. 1 коэффициенты Стьюдента и вычислить погрешность аргументов
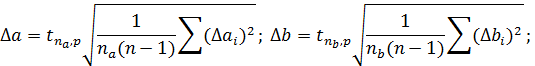
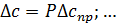
6. Если функция Z=Z(a, b, c, …) удобна для логарифмирования, прологарифмировать ее и по формуле (14) вычислить погрешность

7. Вычислить предварительный результат измерения
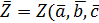 ,…).
,…).
8. Округлить погрешность и результат измерений, записать его в виде 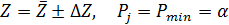 .
.
НЕВОСПРОИЗВОДИМЫЕ КОСВЕННЫЕ ИЗМЕРЕНИЯ
Иногда при выполнении косвенных измерений наблюдения невозможно повторить в тождественных условиях относительно одного или нескольких аргументов измеряемой функции. Например, в измерениях коэффициента вязкости жидкости в нее бросают металлические шарики (дробинки). Каждый из брошенных в жидкость шариков достать обратно сразу же нельзя. Повторение же опыта с другим шариком не будет тождественно первому эксперименту из-за различия формы шариков, состояния их поверхностей и т.д. В этом случае говорят, что косвенные измерения невоспроизводимы.
Для невоспроизводимых косвенных измерений рекомендуется следующий порядок обработки их результатов:
1. Определить значение искомой функции Z (a, b, c, …) для каждого i -го невоспроизводимого наблюдения, исходя из найденных экспериментальных значений аргументов 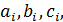 ….
….
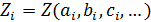
2. Каждое из определенных таким образом значений 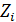 рассматривается как результат прямого (многократного) измерения физической величины Z. В соответствии с этим погрешность вычисляется аналогично формуле (4)
рассматривается как результат прямого (многократного) измерения физической величины Z. В соответствии с этим погрешность вычисляется аналогично формуле (4)
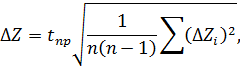
т.е. по правилам обработки результатов прямых многократных измерений.
ВЫЧИСЛЕНИЯ. ОКРУГЛЕНИЕ ПОГРЕШНОСТЕЙ И РЕЗУЛЬТАТА ИХМЕРЕНИЙ. ЗАПИСЬ РЕЗУЛЬТАТА
Все предварительные расчеты результата измерений следует производить не более, чем до 3-4 значащих цифр.
Погрешность достаточно предварительно вычислить до 2 значащих цифр, а затем сразу же округлить до одной значащей цифры.
Примеры
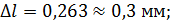
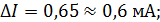
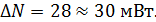
Данное правило объясняется тем, что при небольшом числе наблюдений (как правило, оно не более 5) значение погрешности определяется весьма приближенно, и нет особого смысла сохранять в ее записи большее число значащих цифр. К тому же, если, например, погрешность составляет сотые доли единицы измеряемой величины, то логично считать, что более мелкими долями можно пренебречь.
Разряды последних производимых в окончательной записи значащих цифр результата и его погрешности должны совпадать
Примеры
| Верно | Неверно |
| R = (3,9 ± 0,2)∙106 Ом. | R = (3,94 ± 0,2)∙106 Ом |
| I = (16,7 ± 0,8) мкА. | I = (17 ± 0,8) мкА. |
| h = (4,60 ± 0,05) см. | h = 4,6 ± 5∙10-2 см. |
Значение относительных погрешностей 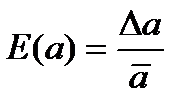 (или
(или 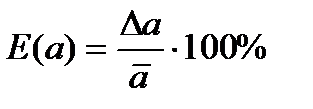 ) достаточно вычислить до двух значащих цифр.
) достаточно вычислить до двух значащих цифр.
ПОРЯДОК ПРОВЕДЕНИЯ КОСВЕННЫХ ИЗМЕРЕНИЙ. ЗАПИСЬ И ОБРАБОТКА РЕЗУЛЬТАТОВ (примеры)
Пример 1
Линейный коэффициент температурного расширения твердых тел (полимеров) определяется выражением
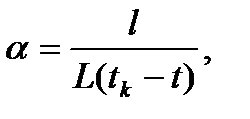 (15)
(15)
| где L – | длина исследуемого образца при комнатной температуре t, |
| l – | удлинение образца, взятое при температуре кипения воды t=tk по отношению к его длине L. |
Для получения расчетной формулы погрешности учтем, что выражения (15) относительно удобно для логарифмирования (содержит три множителя l, L, (tk – t)) и, следовательно, целесообразно искать погрешность по формуле (14) с учетом замены соответствующих обозначений функции и аргументов:
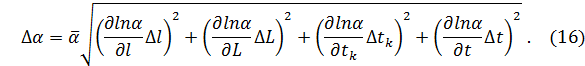
Производя логарифмирование выражения (15) получаем
lnα=lnl – lnL – ln(tk-t).
Находим частные производные
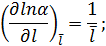
| 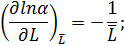
|
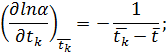
| 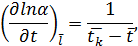
|
где 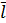 ,
, 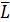 ,
, 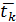 и
и 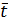 – средние значения соответствующих параметров, которые необходимо найти экспериментально. Выражение для расчета погрешности
– средние значения соответствующих параметров, которые необходимо найти экспериментально. Выражение для расчета погрешности  α, тогда
α, тогда
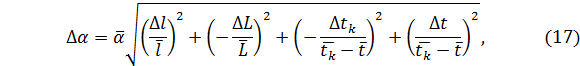
где ∆l, ∆L, ∆tk, ∆t –погрешность аргументов, взятые с некоторой вероятностью P.
По условиям эксперимента путем многократных прямых измерений определяется всего одна величина – первоначальная (при комнатной температуре t) длина образца L.
В табл.4 предусматривающей также частичную обработку результатов, приведены значения длины Li, некоторого полимерного стержня, измеренные штангенциркуле с ценой деления 0,1 мм.
Таблица 4.
| |||||||||||||||||||||||||||
| Paт = 774 мм рт. ст., | |||||||||||||||||||||||||||
| l =(1,32 ± 0,01) мм, P =1 | |||||||||||||||||||||||||||
tk =(101,240 ± 0,005) 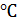 , P =1 , P =1
| |||||||||||||||||||||||||||
t =(24 ± 1) 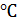 , P =1 , P =1
| |||||||||||||||||||||||||||
Слева от табл. 4 даны значения однократно измеряемых параметров l, tk, t (удлинение нагретого образца, температура кипения воды, найденная по таблице ее взаимосвязи с атмосферным давлением P ат, и комнатная температура соответственно) и указаны их предельные погрешности (P = 1). Предельная погрешность удлинения ∆l пр = 0,01мм найдена как предельная погрешность прибора (ПРТТ), цена деления которого равна 0,01 мм. Предельная погрешность температуры кипения воды (∆t к ) пр = 0,005 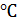 определена как предельная погрешность ее табличного значения t к = 101,24
определена как предельная погрешность ее табличного значения t к = 101,24 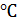 . Наконец, предельная погрешность измерения комнатной температуры ∆t пр = 1
. Наконец, предельная погрешность измерения комнатной температуры ∆t пр = 1 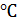 найдена как предельная погрешность лабораторного термометра с ценой деления 1
найдена как предельная погрешность лабораторного термометра с ценой деления 1 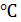 .
.
Предельная приборная погрешность измерения длины L как предельная погрешность штангенциркуля с ценой деления 0,1 мм (по нониусу) также равна ∆L 1= 0,1 мм.
Оценивая вероятность P по результатам многократного измерения длины L, согласно формуле (3), получаем
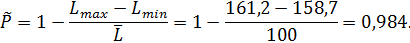
За окончательное значение вероятности результата измерений выбираем вероятность P =0,98 (как ближайшую в табл.1 к найденному ее оценочному значению 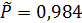 ).
).
По данным табл.4, в соответствии с обработкой результатов прямых многократных измерений находим
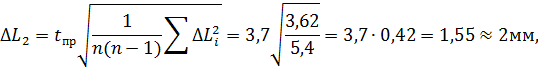
где, согласно табл.1, коэффициент Стьюдента t 5; 0,98 = 3,7. Найденная погрешность среднего ∆L 2 = 2 мм существенно превосходит приборную погрешность ∆L 1= 0,1 мм. Следовательно, результирующая погрешность измерения длины L равна ∆L = ∆L 2 = 2 мм, P = 0,98.
Примем вероятность P = 0,98 как общую вероятность результата измерений. Тогда погрешности аргументов, в силу приведенных правил округления погрешностей, фактически не изменят своих предельных значений. Действительно,
∆ l = P∆ l пр = 0,98∙0,01 = 0,0098 ≈ 0,01 мм, P = 0,98;
∆ t к = P∙(∆ t к)пр = 0,98∙0,005 = 0,0049 ≈ 0,005 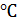 , P = 0,98;
, P = 0,98;
∆ t = P∙∆ t пр = 0,98∙1 = 0,98 ≈ 1 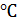 , P = 0,98.
, P = 0,98.
Учитывая измеренные значения величин 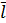 ,
, 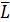 ,
, 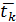 и
и 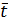 , по формуле (15) вычисляем предварительный результат
, по формуле (15) вычисляем предварительный результат
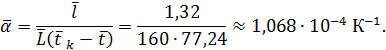
По формуле (17) записываем погрешность
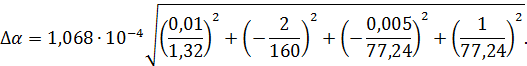
Оценивая здесь члены подкоренного выражения, находим, что 2-й и 4-й фактически равны друг другу, а остальными можно пренебречь, так как они меньше на 2-3 порядка. Это дает
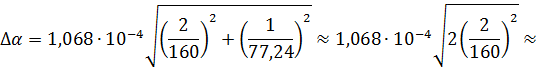
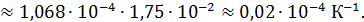
Окончательный результат измерения коэффициента линейного расширения полимерного образца может быть записан в виде
α = (1,07±0,02)∙10 – 4 К-1, P = 0,98.
Пример 2
В одной из лабораторных работ с помощью маятника Атвуда проверяется справедливость закона сохранения механической энергии. Расчетная формула работы имеет следующий вид
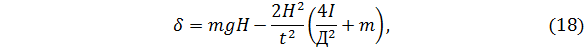
| где | 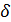
| - разность механических энергий изолированной системы для некоторых двух моментов, разделенных промежутком времени t; |
| m | - масса груза, приводящего систему в движение; | |
| g | - ускорение свободного падения (на широте Санкт-Петербурга); | |
| H | - высота груза m над полом в исходном положении; | |
| t | - время падения груза на пол; | |
| I | - момент инерции маятника Атвуда; | |
| Д | - диаметр шкива (вала), на который наматывается нить в маятнике Атвуда. |
Выражение (18) явно неудобно для логарифмирования, поэтому ищем погрешность ∆ 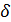 по формуле (12), заменяя в ней обозначения на отвечающие выражению (18)
по формуле (12), заменяя в ней обозначения на отвечающие выражению (18)
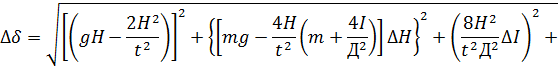
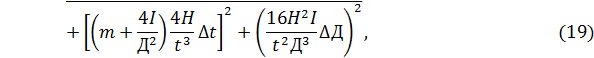
| где | 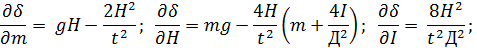

|
частные производные функции 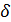 по аргументам m, H, t, I, Д. Погрешностью ускорения свободного падения ∆ g пренебрегаем в силу ее очевидной малости.
по аргументам m, H, t, I, Д. Погрешностью ускорения свободного падения ∆ g пренебрегаем в силу ее очевидной малости.
По условиям эксперимента путем многократных прямых измерений допустимо определять всего одну величину – время падения груза. В табл. 5 даны результаты одной из серий измерения этой величины. Слева от табл. 5 указаны результаты однократных измерений аргументов H, m, I, g, Д. Часть из них указана преподавателем, часть – находиться по таблицам. Здесь же указаны предельные погрешности данных величин (P = 1).
| Таблица 5. | ||||||||||||||||||||||||||||||||||
| Результаты измерения времени | ||||||||||||||||||||||||||||||||||
| H = (1,30 ± 0,01) м, g = (9,820 ±,005) м/с2, m = (0,400 ± 0,001) кг, I = (2,96 ± 0,08)∙10-2 кг∙м2, Д = (35,0 ± 0,1) мм, P = 1 |
| |||||||||||||||||||||||||||||||||
По данным табл. 5 и по формуле (3) оцениваем вероятность измеренного значения времени t
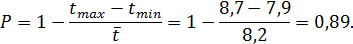
Ближайшее из табл. 1 значение вероятности P = 0,9 принимаем за окончательное.
По данным табл. 5 погрешность среднего для времени
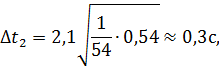
где коэффициент Стьюдента tnp = t 5; 0,9 = 2,1 (см. табл.1). Погрешность среднего ∆ t 2 и приборная погрешность ∆ t 1 = 0,3 с (табл. 3) равны, поэтому окончательная погрешность ∆ t измерения времени t равна
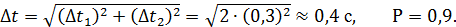
Погрешность аргументов H, m, I, Д, t с вероятностью P = 0,9, выраженные в СИ, тогда
∆ H = P∙∆Hпр = 0,9 ∙ 10-2 = 9∙10-3 м,
∆ m = P∙∆mпр = 0,9 ∙ 10-3 = 9∙10-4 кг,
∆ I = P∙∆Iпр = 0,9 ∙ 0,08 ∙ 10-2 = 7∙10-4 кг∙м2,
∆Д = P∙∆ Д пр = 0,9 ∙ 10-4 = 9∙10-5 м,
∆ t 1 = P∙∆tпр = 0,9 ∙ 0,3= 0,3 с.
Подставляя найденные значения аргументов и их погрешностей в формулу (19) (обязательно выразив все величины в СИ), находим погрешность ∆δ результата измерений
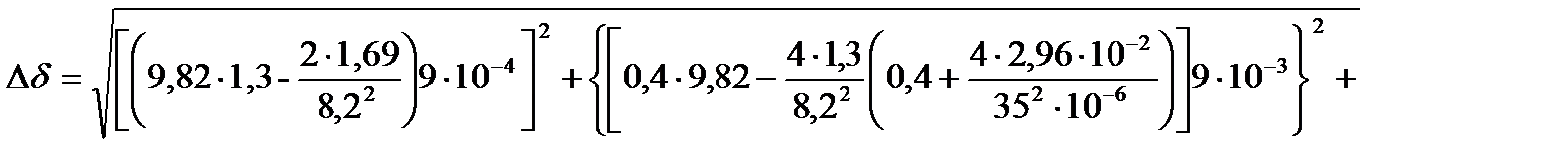
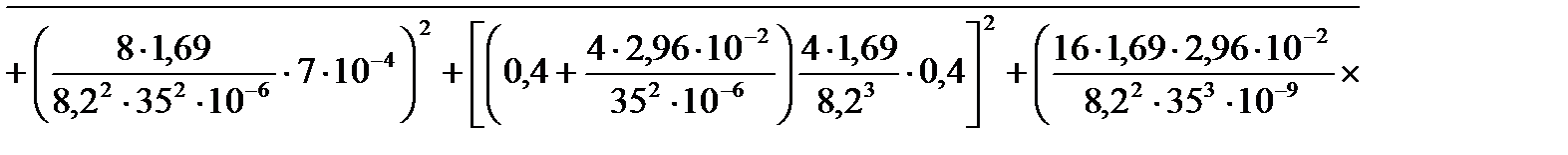

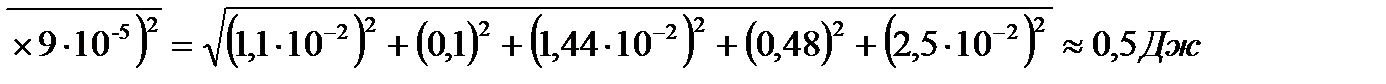 .
.
Видно, что погрешность ∆δ в данном случае целиком определяется погрешностью ∆ t измерения времени t.
Подставляя в формулу (18) измеренные значения аргументов, выраженные в СИ, вычисляемрезультат

Округляя полученное значение 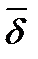 в соответствии с найденной погрешностью ∆δ, запишем окончательный результат
в соответствии с найденной погрешностью ∆δ, запишем окончательный результат
δ = (0,2 ± 0,5) Дж, P = 0,9,
что полностью соответствует закону сохранения механической энергии изолированной системы, изучаемому в данной работе.
Пример 3
В лабораторном экспериме
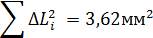
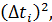 c2
c2
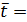 8,2 c
8,2 c
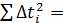 0,54 c2
0,54 c2