Лекальные и коробовые кривые

Тема: Геометрические построения и приемы вычерчивания контуров технических деталей.

План занятия:

Построение сопряжений, применяемых в технических деталях.

Эллипс, синусоида, спираль Архимеда, эвольвента окружности и др.

Построение сопряжений, применяемых в технических деталях.

Некоторые детали имеют равномерно расположенные окружности или другие элементы, для построения которых нужно делить заданную окружность на равные части.

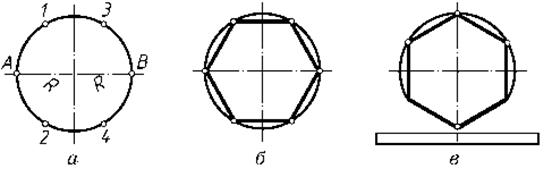
Для того чтобы разделить окружность на три равные части, нужно принять за центр точку пересечения окружности с одним из диаметров и провести из нее дугу, радиус которой R равен радиусу изображенной окружности (рис. 1.1, а). Полученные точки 1 и 3 вместе с точкой 2 разделяют заданную окружность на три равные части. Соединив точки 1, 2 и 3 прямыми, получим вписанный треугольник (рис. 1.1, б).

Два взаимно перпендикулярных диаметра делят окружность на четыре равные части. Соединив точки 1, 2, 3 и 4 прямыми (рис. 1.1,в), получим вписанный четырехугольник.

Рисунок 1.1

а б в

На шесть равных частей окружность делят так. Приняв за центры дуг точки пересечения одного из диаметров с окружностью - А и В, проводят две дуги радиусом R, равным радиусу изображенной окружности (рис. 1.2, а). Эти дуги пересекают окружность в четырех точках 1, 2, 3 и 4. Вместе с точками А и Б они делят окружность на шесть равных частей (рис. 1.2, б). Ту же задачу можно решить при помощи угольника с углами 30° и 60° и линейки (рис. 1.2, в).

Рисунок 1.2

На рисунке 59, а показано деление окружности на восемь равных частей. Для этой цели дуги 1-3, 3-5 и др. делят пополам точками 2, 4 и т. д. или делят на две равные части отрезки 1-3, 3-5 и т. д. Можно поступить так: провести через центр окружности две пары взаимно перпендикулярных диаметров (рис. 1.3, б).

Рисунок 1.3

На пять равных частей окружность можно разделить с помощью циркуля и линейки (рис. 1.4, а). Если разделить радиус ОА окружности пополам (точка К), провести из точки К дугу радиусом КС до пересечения ее с диаметром окружности (точка М), то отрезок СМ и будет стороной вписанного пятиугольника. Последовательно откладывая полученный отрезок на окружности, можно получить точки, которые разделят окруж-ность на пять равных частей.

Эту графическую задачу можно решить и так: пятой части окружности соответствует угол в 72° (360°: 5 = 72°); такой угол можно построить с помощью транспортира (рис. 1.4, б).

Рисунок 1.4

Сопряжения

Сопряжением называется плавный переход по кривой от одной ли­нии к другой. Сопряжения бывают циркульные и лекальные. Построение их основано на свойствах касательных к кривым линиям. Сопряжение отрезков прямых с циркульными кривыми будет возможно, если точка сопряжения является одновременно и точкой касания прямой к дуге кривой. Следовательно, радиус сопряжения должен быть перпендику­лярным к прямой в точке касания.

Роль плавных переходов в очертаниях различных изделий техники огромна. Их обуславливают требования прочности, гидроаэродинами­ки, промышленной эстетики и технологии.

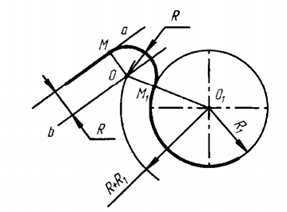
На рисунке 1.1 показано сопряжение дуги окружности радиусом Л, и прямой линии а дугой окружности радиуса R с внешним касанием.

Параллельно заданной прямой на расстоянии, равном радиусу R (ра­диус сопрягаемой дуги), проводят прямую b. Из центра О, проводят дугу окружности радиусом, равным сумме радиусов R и R₁, до пересечения ее с прямой Ь в точке О. Точка О является центром дуги сопряжения. Точку сопряжения М₁ находят на пересечении прямой ОО₁ с дугой окружности радиуса R₁ Точка сопряжения М является основанием пер­пендикуляра, опущенного из центра О на данную прямую а.

На рисунке 1.2 показан пример, при вычерчивании которого необ­ходимо построение внутреннего и внешнего сопряжения. При внутрен­нем сопряжении (рисунок 1.2, а) центры O₂ и O₁ сопрягаемых дуг нахо­дятся внутри сопрягающей дуги радиуса R. При внешнем сопряжении (рисунок 1.2, б) центры O₂ и О₁ сопрягаемых дуг радиусов R₁ и R₂ нахо­дятся вне сопрягающей дуги радиуса R.

Рисунок 1.2

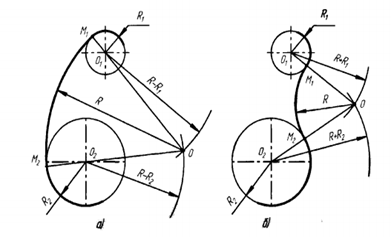
На рисунке 1.2 показан пример, при вычерчивании которого необ­ходимо построение внутреннего и внешнего сопряжения. При внутрен­нем сопряжении (рисунок 1.2, а) центры O₂ и O₁ сопрягаемых дуг нахо­дятся внутри сопрягающей дуги радиуса R. При внешнем сопряжении (рисунок 1.2, б) центры O₂ и О₁ сопрягаемых дуг радиусов R₁ и R₂ нахо­дятся вне сопрягающей дуги радиуса R.

Для построения внутреннего сопряжения должны быть заданы ра­диусы сопрягаемых окружностей R₁ и R₂, положение точек центров О, и O2 этих окружностей, радиус R сопрягающей дуги.

Требуется определить положение центра О сопрягающей дуги, и найти точки сопряжения M1 и М2.

На чертеже намечают центры O2 и O1, из которых описывают сопря­гаемые дуги радиусов R1 и R2. Из центра О, проводят вспомогательную дугу окружности радиусом, равным разности радиусов сопрягающей дуги R и сопрягаемой R₁, а из центра O₂ — радиусом, равным разности радиусов сопрягающей дуги R и сопрягаемой R₂. Вспомогательные дуги пересекутся в точке О, которая и будет искомым центром сопрягающей дуги. Для нахождения точек сопряжения точку О соединяют с точками O₂ и О, прямыми линиями. Точки пересечения продолжения прямых O₂ О и OO₁, с сопрягаемыми дугами являются искомыми точками сопряжения (точки М₂ и М₁). Радиусом R из центра О проводят сопрягающую дугу между точками сопряжения М₂ и M₁. Для построения внешнего сопряжения с теми же исходными данны­ми из центра О₁ проводят вспомогательную дугу окружности радиусом, равным сумме радиусов сопрягаемой дуги R₁, и сопрягающей R, а из центра O₂ — радиусом, равным сумме радиусов сопрягаемой дуги R₂ и сопрягающей R. Вспомогательные дуги пересекутся в точке О, которая будет искомым центром сопрягающей дуги. Для нахождения точек со­пряжения центры дуг соединяют прямыми линиями OO₂ и O₁O. Эти две прямые пересекают сопрягаемые дуги в точках сопряжения М₂ и М₁. Из центра О радиусом R проводят сопрягающую дугу, ограничивая ее точками сопряжения M₁ и М₁.

Лекальные и коробовые кривые

Лекальные кривые имеют большое применение в технике. Рассмотрим наиболее часто встречающиеся способы построения плоских кривых. Эти кривые обычно обводят с помощью лекал, поэтому они получили название лекальных кривых.

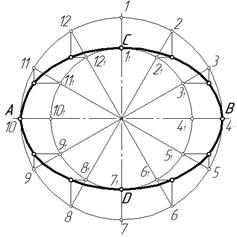
Эллипс представляет собой замкнутую плоскую кривую второго порядка. Она характеризуется тем, что сумма расстояний от любой ее точки до двух точек фокусов есть величина постоянная, равная большей оси эллипса. Построить эллипс можно несколькими способами. Например, можно построить эллипс по его большой АВ и малой CD осям (рисунок 2.1) На осях эллипса как на диаметрах строят две окружности, которые можно разделить радиусами на несколько частей. Через точки деления большой окружности проводят прямые, параллельные малой оси эллипса, а через точки деления малой окружности - прямые, параллельные большой оси эллипса. Точки пересечения этих прямых и являются точками эллипса.

Рисунок 2.1

Синусоида. Синусоидой называется проекция траектории точки, движущейся по цилиндрической винтовой линии, на плоскость, параллельную оси цилиндра. Движение точки складывается из равномерно–вращательного движения (вокруг оси цилиндра) и равномерно–поступательного (параллельно оси цилиндра). Синусоида – это плоская кривая, которая показывает изменение тригонометрической функции синуса в зависимости от изменения величины угла.

Для построения синусоиды (рисунок 2.2) через центр О окружности диаметра D проводят прямую ОХ и на ней откладывают отрезок O1A, равный длине окружности 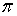D. Этот отрезок и окружность делят на одинаковое число равных частей. Из полученных и занумерованных точек проводят взаимно перпендикулярные прямые. Полученные точки пересечения этих прямых соединяют с помощью лекала плавной кривой.

Рисунок 2.2

Спираль Архимеда. Для построения спирали Архимеда задается шаг спирали – а, и центр О. Из центра О описывают окружность радиусом Р = а. Делят окружность на несколько равных частей, например, на восемь (точки 11 21, …, 81). На столько же частей делят отрезок О81 (точки 1, 2, …, 8).

Рисунок 2.3

Из центра О радиусами О1, О2, и т.д. проводят дуги окружности, точки А1, А2, … пересечения которых с соответствующими радиусами-векторами принадлежат спирали, так, например дуга, проведенная через точку 3, пересекается с радиусом-вектором, проходящим через точку 31, в точке А3, принадлежащей спирали.(рисунок 2.3)

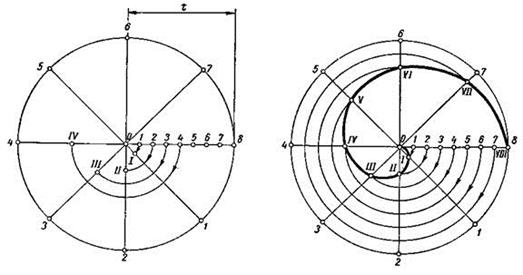
Эвольвента окружности. Имеется окружность с диаметром , и с центром в точке . Данную окружность делим на двенадцать равных частей. В точках 2, 3, 4, … проводим касательные к окружности, направленные в одну сторону. Точки эвольвенты находим исходя из того, что при развёртывании окружности точка , должна отстоять от точки 2 на расстоянии, равном длине дуги между точками 1 и 2, а точка 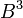, должна отстоять от точки 3 на расстоянии, равном длине дуги между точками 1 и 3 (две длины предыдущей дуги), и т. д.

Рисунок 2.4

Точное положение точек эвольвенты получим, откладывая по касательным длины соответствующих дуг. Длину дуги между точками 1 и 2 определяем по формул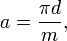е , где — диаметр окружности; — число частей, на которое разделена окружность.

Получив ряд точек эвольвенты соединяем их плавной линией.

В данном случае окружность с диаметром является эволютой к этой эвольвенте. (рисунок 2.4)