методом замены плоскостей проекций

методом замены плоскостей проекций

Расстоянием между двумя точками называется длина отрезка, соединяющего эти точки. Отрезок общего положения не параллелен ни одной из плоскостей проекций. Длины проекций А ₁ В ₁ и А ₂ В ₂ меньше длины отрезка АВ. Для того чтобы узнать длину отрезка АВ, необходимо спроецировать его в натуральную величину и измерить эту проекцию, так как она равна отрезку АВ.

Рис. 32 Определение длины отрезка

Введем новую плоскость проекций П ₄ параллельно отрезку АВ (рис. 32) и перпендикулярно П ₁. При этом новая ось x₁₄ будет параллельна А ₁ В ₁ (в противном случае прямая АВ и плоскость П ₄ пересекутся). Угол наклона отрезка АВ к плоскости П ₄ равен нулю, и АВ на П ₄ проецируется в натуральную величину, т.е. А ₄В₄ = АВ. Измерив отрезок А ₄ В ₄, получим длину отрезка АВ.

 

Выявление натуральной величины плоской фигуры

методом замены плоскостей проекций

Пусть ∆ ABC – плоскость общего положения (рис. 33). В плоскости треугольника проведем горизонталь h, спроецируем горизонталь h в точку h ₄ на плоскость П ₄ (x ₁₄ ⊥ h ₁, П₄ ⊥ h), построим новые проекции точек А ₄, В ₄, С ₄. Плоскость ∆ ABC проецируется в прямую, проходящую через точки А ₄, В ₄, С ₄. Плоскость треугольника в системе (П ₁ П ₄) является проецирующей плоскостью, она перпендикулярна П ₄. Треугольник АВС проецируется на П ₄ в отрезок В ₄ С ₄.

Для нахождения натуральной величины ∆ АВС введем плоскость проекций П ₅ параллельно плоскости треугольника и перпендикулярно П ₄. Новая ось x ₄₅ параллельна отрезку D ₄ C ₄ (в противном случае ∆ ABC и П ₅ пересекутся). Треугольник АВС проецируется на плоскость П ₅ в натуральную величину Δ А ₅ В ₅ С ₅ = Δ АВС.

Аналогично находится натуральная величина любой плоской фигуры.

 

Рис. 33 Определение натуральной величины плоскости

Практическое задание № 3. Выполните чертеж двух пересекающихся плоскостей (формат А4).

Рис. 34 Образец выполнения практического задания № 3

Тема 4

ПОВЕРХНОСТИ

 

Начертательная геометрия изучает кинематический способ образования и задания поверхностей. При этом поверхность рассматривают как множество последовательных положений движущейся линии или другой поверхности в пространстве. Линию, перемещающуюся в пространстве и образующую поверхность, называют образующей. Образующие могут быть прямыми и кривыми. Кривые образующие могут быть постоянными и переменными, например, закономерно изменяющимися.

Закон перемещения образующей обычно определяется другими линиями, называемыми направляющими, по которым скользит образующая при своем движении, а также характером движения образующей. В некоторых случаях одна из направляющих может превращаться в точку, например, вершина у конической поверхности, или находиться в бесконечности, например, у цилиндрической поверхности.

Совокупность геометрических элементов, определяющих поверхность, называют определителем поверхности, учитывая, что закон перемещения образующей определяется названием поверхности.

Задание поверхности проекциями ее определителя не всегда обеспечивает наглядность, а это, в свою очередь, затрудняет чтение чертежа, поэтому для получения наглядного изображения поверхности на комплексном чертеже следует указывать очерк этой поверхности. Очерк проекции поверхности является проекцией соответствующей линии видимого контура. Линия видимого контура поверхности разделяет ее на две части – видимую, обращенную к наблюдателю, и невидимую.

Классификация поверхностей

Классифицируют поверхности, как правило, в зависимости от формы образующей и закона ее перемещения в пространстве (рис. 35):

Поверхность называется линейчатой, если она может быть образована перемещением прямой линии. Поверхность, которая не может быть образована движением прямой линии, называется нелинейчатой. Например, конус вращения – линейчатая поверхность, а сфера – нелинейчатая. Через любую точку линейчатой поверхности можно провести, по крайней мере, одну прямую, целиком принадлежащую поверхности. Множество таких прямых представляет собой непрерывный каркас линейчатой поверхности. Линейчатые поверхности разделяются на два вида:

– развертывающиеся поверхности;

– неразвертывающиеся, или косые поверхности.

Поверхность называется развертывающейся, если она может быть совмещена с плоскостью без образования складок и разрывов.

Неразвертывающиеся поверхности невозможно совместить с плоскостью без образования складок и разрывов.

Гранные поверхности

Поверхность, образованная частями попарно пересекающихся плоскостей, называется многогранной. На рис. 36 изображены некоторые виды гранных поверхностей.

а б в

 

Рис. 36 Гранные поверхности

 

Их элементами являются грани, ребра и вершины. Плоскости, образующие многогранную поверхность, называются гранями, линии пересечения смежных граней – ребрами, точки пересечения не менее чем трех граней – вершинами.

Гранная поверхность называется пирамидальной, если все ее ребра пересекаются в одной точке – вершине (рис. 36 а). Гранная поверхность называется призматической, если все ее ребра параллельны между собой (рис. 36 б). Геометрическое тело, со всех сторон ограниченное плоскими многоугольниками, называется многогранником. Призматоидом называется многогранник, у которого верхнее и нижнее основания – многоугольники, расположенные в параллельных плоскостях, а боковые грани представляют собой треугольники или трапеции (рис. 36 в).

 

Торсовые поверхности

Торсовой называют поверхность, образованную при движении прямолинейной образующей по криволинейной направляющей.

Существует три вида таких поверхностей: торсы, конические и цилиндрические поверхности (рис. 37).

Цилиндрическая поверхность (рис.37 а) образуется движением прямой линии, скользящей по некоторой неподвижной замкнутой или незамкнутой кривой и остающейся параллельной своему исходному положению. Множество прямолинейных образующих представляет собой непрерывный каркас цилиндрической поверхности. Через каждую точку поверхности проходит одна прямолинейная образующая.

 

а б в

Рис. 37 Поверхности: торсовая цилиндрическая, торсовая коническая, торс

Часть замкнутой цилиндрической поверхности, заключенная между двумя плоскими параллельными сечениями, называется цилиндром, а фигуры сечения – его основаниями.

Коническая поверхность (рис.37 б) образуется движением прямой линии, скользящей по некоторой неподвижной замкнутой или незамкнутой кривой и проходящей во всех своих положениях через неподвижную точку.

Конусом называется Часть замкнутой конической поверхности, ограниченная вершиной и какой-либо плоскостью, пересекающей все ее образующие. Фигура сечения конической поверхности этой плоскостью называется основанием конуса.

Поверхности с плоскостью параллелизма

Поверхности с плоскостью параллелизма в общем случае образуются движением прямолинейной образующей по трем направляющим линиям, которые однозначно задают закон ее перемещения.

Направляющие линии могут быть кривыми и прямыми. Разновидностями косых поверхностей являются линейчатые поверхности с направляющей плоскостью и частные их виды - линейчатые поверхности с плоскостью параллелизма (поверхности Каталана).

Поверхности с плоскостью параллелизма в аналогичных случаях соответственно называются прямыми цилиндроидами, прямыми коноидами и косой плоскостью.

Прямым цилиндроидом (рис. 38) называется поверхность, образованная движением прямой линии, скользящей по двум криволинейным направляющим, не принадлежащим одной плоскости, и остающейся во всех своих положениях параллельной некоторой заданной плоскости. Эта плоскость называется плоскостью параллелизма.

Прямым коноидом (рис. 39) называется поверхность, образованная движением прямой линии, скользящей по двум направляющим, одна из которых – кривая, а вторая – прямая, и остающейся во всех своих положениях параллельной некоторой плоскости параллелизма.

Рис. 38 Прямой цилиндроид Рис. 39 Прямой коноид Рис. 40 Косая плоскость

 

Косой плоскостью (рис. 40) называется поверхность, образованная движением прямой линии, скользящей по двум скрещивающимся прямым и остающейся во всех своих положениях параллельной некоторой плоскости параллелизма.

 

Винтовые поверхности

Поверхность, образованная винтовым движением прямой линии, называется линейчатой винтовой поверхностью – геликоидом (винтовое движение характеризуется вращением вокруг некоторой оси i и поступательным перемещением, параллельным этой оси).

а б

Рис. 41 Винтовые поверхности

 

Если в качестве кривой направляющей коноида взять цилиндрическую винтовую линию, в качестве прямой направляющей – ось винтовой линии, а за плоскость параллелизма – плоскость, перпендикулярную оси винтовой линии, то поверхность, образованная при этих условиях, называется винтовым коноидом или прямым геликоидом (рис. 41 а).

Наклонным геликоидом называется поверхность, образованная движением прямой линии, cкользящей по двум направляющим (одна из них цилиндрическая винтовая линия, а вторая – ось винтовой линии) и сохраняющей во всех положениях постоянный угол β _С направляющей плоскостью, которую располагают перпендикулярно оси винтовой поверхности. При построении проекций наклонного геликоида удобно пользоваться направляющим конусом (рис. 41 б).

 

Поверхности вращения

Если перемещение образующей линии представляет собой вращение вокруг некоторой неподвижной прямой (оси), то образованная в этом случае поверхность называется поверхностью вращения.

Образующая линия может быть плоской или пространственной кривой, а также прямой. Каждая точка образующей линии при вращении вокруг оси описывает окружность, которая располагается в плоскости перпендикулярной оси вращения (рис. 42).

Эти окружности называются параллелями. Следовательно, плоскости, перпендикулярные оси, пересекают поверхность вращения по параллелям. Линия пересечения поверхности вращения плоскостью Σ, проходящей через ось, называется меридианом.

Меридиан, который является результатом пересечения поверхности вращения с плоскостью уровня, называется главным. Проекция главного меридиана на плоскость, которой параллельна плоскость уровня, является очерковой линией соответствующей проекции поверхности вращения.

Рис. 42 Элементы поверхности вращения

Множество всех параллелей или меридианов представляет собой непрерывный каркас поверхности вращения. Через каждую точку поверхности проходит одна параллель и один меридиан. Проекции точки располагаются на соответствующих проекциях параллели или меридиана. Задать точку на поверхности или построить вторую проекцию точки, если одна задана, можно при помощи параллели или меридиана, которые проходят через эту точку.

При проектировании различных инженерных сооружений, машин и механизмов наибольшее распространение получили поверхности, образующиеся вращением прямой линии и кривых второго порядка.

Вращением прямой линии образуются:

– цилиндр вращения, если прямая l параллельна оси i (рис. 43 а);

– конус вращения, если прямая l пересекает ось i (рис. 43 б);

– однополостный гиперболоид, если прямая l скрещивается с осью i (рис. 43 в).

а	б	в
Рис. 43 Линейчатые поверхности вращения

К поверхностям вращения, образованным вращением кривых второго порядка вокруг оси относятся:

– сфера образуется вращением окружности вокруг ее диаметра (рис. 44 а);

– эллипсоид вращения образуется вращением эллипса вокруг большой или малой оси (44 б, в);

– тор образуется вращением окружности вокруг внешней оси (рис. 44 г);

а	б	в
г	д	е
Рис. 44 Поверхности вращения второго порядка

– параболоид вращения образуется вращением параболы вокруг ее оси (рис. 44 д);

– однополостный гиперболоид вращения образуется вращением гиперболы вокруг ее мнимой оси. Эта поверхность образуется также вращением прямой (рис. 44 е).

Каналовые и циклические поверхности

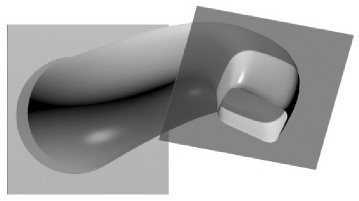
Каналовой называют поверхность, образованную непрерывным каркасом замкнутых плоских сечений, определенным образом ориентированных в пространстве. Площади этих сечений могут оставаться постоянными или монотонно изменяться в процессе перехода от одного сечения к другому. На рис. 45 приведены два изображения каналовой поверхности. В инженерной практике наибольшее распространение получили два способа ориентирования плоскостей образующих:

– параллельно какой-либо плоскости – каналовые поверхности с плоскостью параллелизма;

– перпендикулярно к направляющей линии – прямые каналовые поверхности.

Рис. 45 Каналовые поверхности

Каналовая поверхность может быть использована для создания переходных участков между двумя поверхностями типа трубопроводов, имеющих:

– различную форму, но одинаковую площадь нормального сечения;

– одинаковую форму, но различные площади сечения;

– различную форму и различные площади поперечных сечений.

Циклическую поверхность можно рассматривать как частный случай каналовой поверхности. Она образуется с помощью окружности, центр которой перемещается по криволинейной направляющей. В процессе движения радиус окружности монотонно меняется. Пример циклической поверхности показан на рис. 46.

Трубчатая поверхность относится к группе нелинейчатых поверхностей с образующей постоянного вида и является частным случаем циклической и каналовой поверхностей. Она обладает свойствами, присущими этим видам поверхностей. У циклической поверхности она позаимствовала форму образующей, а у каналовой – закон движения этой образующей. На рис. 47 приведен пример трубчатой поверхности.

Рис. 46 Циклическая поверхность	Рис. 47 Трубчатая поверхность

Графические поверхности

Графические поверхности задаются конечным множеством линий уровня, образующих каркас этих поверхностей. Примеры графических поверхностей представлены на рис. 48.

Рис. 48 Графические поверхности

Пересечение поверхности и плоскости

Линия пересечения поверхности с плоскостью представляет собой линию, называемую сечением. Точки этой кривой можно рассматривать как точки пересечения линий поверхности с плоскостью или прямых плоскости с поверхностью.

Отсюда следуют два варианта построения сечения:

1) выбираем конечное число линий на поверхности и определяем точки пересечения их с плоскостью;

2) выделяем конечное число прямых на плоскости и строим точки пересечения их с поверхностью.

Заметим, что возможно решение, представляющее собой комбинацию этих вариантов. В любом случае построение сечения сводится к многократному применению алгоритма решения задачи на пересечение линии и поверхности.

Определение проекций линий сечения рекомендуется начинать с построения его опорных (характерных) точек. К ним относятся точки, расположенные на очерковых образующих поверхности (они определяют границы видимости проекций кривой), точки, удаленные на экстремальные расстояния от плоскостей проекций и некоторые другие. После этого определяют промежуточные точки сечения.

Построение сечения существенно упрощается, если плоскость занимает проецирующее положение. Это связано с тем, что проецирующая плоскость характеризуется собирательным свойством. В этом случае одна из проекций сечения находится на следе плоскости, т.е. известна.

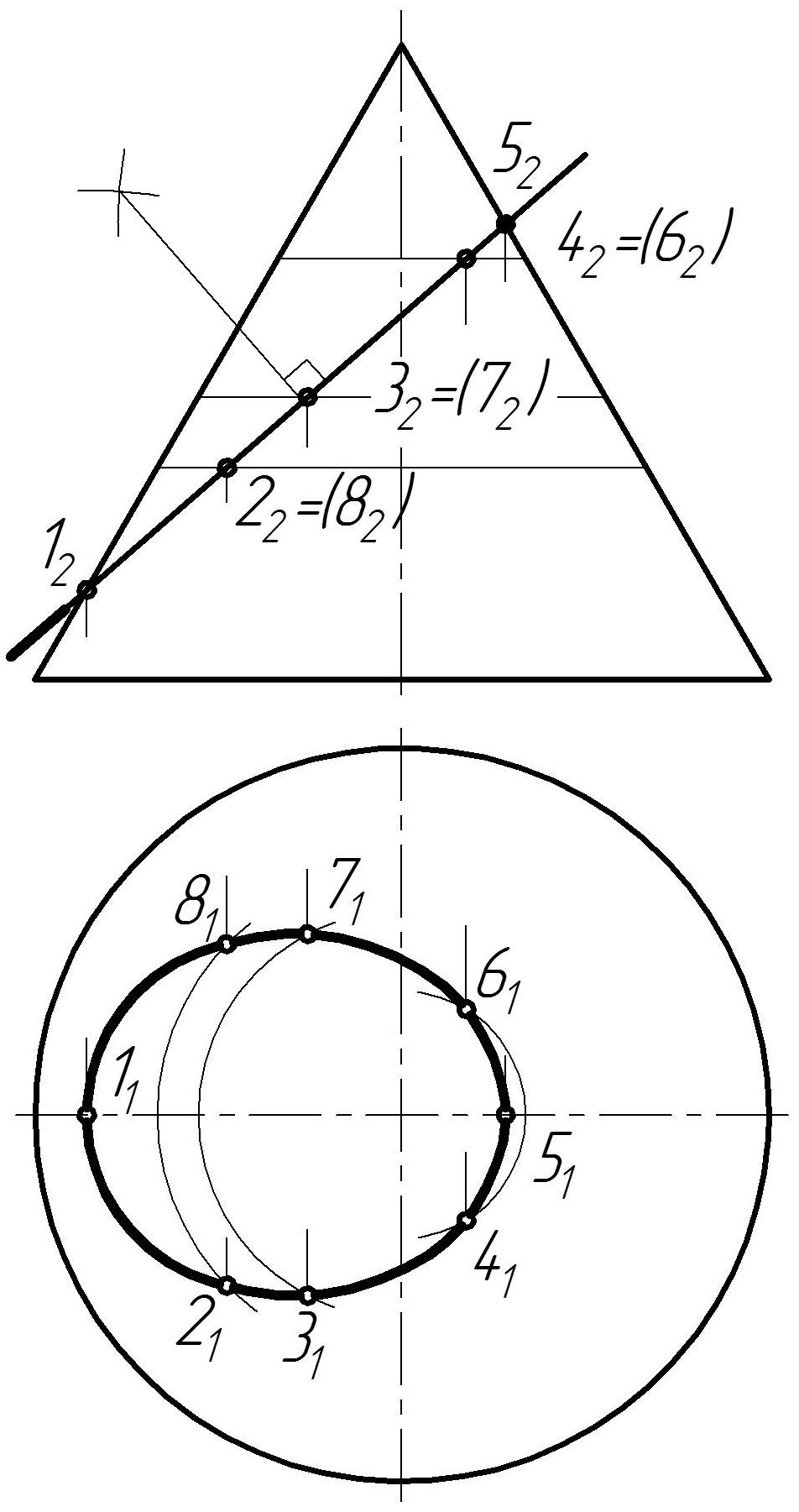
В пересечении гранных поверхностей плоскостями получаются многоугольники (рис. 49 а). Их вершины определяются как точки пересечения ребер гранных поверхностей с секущей плоскостью. Секущая плоскость Σ является фронтально-проецирующей, следовательно, все линии, лежащие в этой плоскости, совпадут с фронтальным следом Σ₂ плоскости Σ. Следовательно, фронтальная проекция 1₂2₂3₂ сечения определится при пересечении фронтальных проекций ребер пирамиды со следом Σ(Σ₂). Горизонтальные проекции точек 1(1₁), 2(2₁) и 3(3₁) находим из условия принадлежности точек ребрам пирамиды.

а б

Рис. 49 Построение линии пересечения поверхности с плоскостью

Построение линии пересечения конической поверхности вращения с фронтально-проецирующей плоскостью Σ показано на рис. 49 б. Заданная плоскость Σ пересекает исходную поверхность по эллипсу, фронтальная проекция которого расположена на следе этой плоскости. Горизонтальную проекцию сечения строим по точкам из условия их принадлежности поверхности конуса (см. рис. 49 б).

 

Практическое задание № 4. Выполните чертеж сферы, усеченной плоскостями частного положения (формат А4).

Рис. 50 Образец выполнения практического задания № 4

Рассмотрим построение выреза сферы, образованного с помощью четырех проецирующих секущих плоскостей (рис.51, а)[1]. Каждая из них пересекает сферу по линии, являющейся частью окружности. Кроме того, Г и Р являются горизонтальной и профильной плоскостями уровня соответственно. Проекции выреза на П ₁ и П ₃ будут симметричными.

 

а	б
в	г

 

Рис. 51 Порядок выполнения практического задания № 4

 

На плоскостях проекций П ₁ и П ₃ ветви выреза от плоскостей Q и Т будут проецироваться в виде частей эллипсов. Точки А и В являются концами осей этих эллипсов.

Отметим опорные точки в плоскостях уровня: 1, 2 и 4 конечные точки ветвей выреза; 5 и 3 точки перемены видимости на плоскостях П ₁ и П ₃ соответственно.

Построим проекции опорных точек частей выреза от секущих плоскостей Г и Р на плоскостях проекций П ₁ и П ₃ (рис. 51, б).

Построим ветвь выреза от плоскости Q. Опорные точки 6 перемена видимости на П ₁. Опорная точка 7 низшая точка (рис. 51, в).

Построим ветвь выреза от плоскости Т. Опорные точки 8 перемена видимости на П ₃. Опорная точка 9 низшая точка (рис. 51, г).

Очерки сферы и видимость линии выреза на плоскостях П ₁ и П ₃ определяются с учетом сквозного выреза.

 

 

Взаимодействие поверхностей между собой

Линия пересечения двух поверхностей представляет собой в общем случае пространственную кривую. Любая точка этой линии принадлежит как первой, так и второй поверхностям и может быть определена в пересечении линий, проведенных на этих поверхностях. Тогда имеем следующие варианты решения данной задачи:

1) выбирают на одной из поверхностей конечное число линий и строят точки пересечения их с другой поверхностью;

2) выделяют на заданных поверхностях два семейства линий и находят их точки пересечения. Во втором варианте выделение пересекающихся пар кривых выполняют с помощью вспомогательных поверхностей посредников.

В качестве поверхностей посредников наиболее часто применяют плоскости или сферы. В зависимости от вида посредников выделяют следующие наиболее часто применяемые способы построения линии пересечения двух поверхностей:

а) способ секущих плоскостей;

б) способ сфер.

 

Способ вспомогательных секущих плоскостей

Рассмотрим применение вспомогательных секущих плоскостей на примере построения линии пересечения сферы с конусом вращения (рис. 52).

Заданные поверхности – поверхности вращения. Оси заданных поверхностей параллельны П ₂, (любой диаметр сферы может быть принят за ось вращения), а их общая плоскость симметрии параллельна фронтальной плоскости проекций. Следовательно, на заданных поверхностях можно выделить два семейства окружностей, расположенных в плоскостях, параллельных горизонтальной плоскости проекций. Это значит, что для решения данной задачи можно использовать в качестве посредников горизонтальные плоскости уровня.

Характерными точками проекций линии пересечения поверхностей являются точки Α, Β и С, D. Точки Α, Β находятся в пересечении очерковых образующих поверхностей, т.к. эти образующие расположены в одной секущей плоскости Ф, проходящей по плоскости симметрии поверхностей. Α и Β высшая и низшая точки линии пересечения. Точки С и D являются точками видимости горизонтальной проекции линии пересечения. Их построения выполнены в такой последовательности:

1) через центр сферы О проведена горизонтальная плоскость уровня Θ;

2) построена горизонтальная проекция окружности радиуса R ¹, по которой плоскость Θ пересекает коническую поверхность; эта же плоскость пересекает сферу по экватору (окружности максимального радиуса);

 

 

Рис. 52 Применение способа вспомогательных секущих плоскостей

3) построена горизонтальная проекция окружности радиуса R ¹, по которой плоскость Θ пересекает коническую поверхность; эта же плоскость пересекает сферу по экватору (окружности максимального радиуса);

4) определены точки C ₁, D ₁ пересечения окружности радиуса R ¹ с очерком сферы;

5) установлены фронтальные проекции точек С (С ₂), D (D ₂) из условия принадлежности их плоскости Θ.

Для построения промежуточных точек 1(1₁,1₂), 2(2₁,2₂), …, 6(6₁,6₂) линии пересечения заданных поверхностей используем плоскости , и .

Полученные точки соединим плавной кривой линией. Видимость линии пересечения определяется в каждой плоскости проекций.

Затем устанавливаются участки, видимые одновременно для обеих поверхностей. Так, при проецировании коническая поверхность своих точек не закрывает, а сфера закрывает точки, расположенные ниже горизонтального контура. Точки С и D, расположенные на горизонтальном очерке, отделяют видимую часть линии от невидимой. Невидимая часть показана штриховой линией. На П ₂ проекции видимой части линии пересечения совпадает с проекцией невидимой, так как фронтальные очерки обеих поверхностей расположены в плоскости симметрии поверхностей.

 

Способ концентрических сфер

Этот способ широко используется при решении задач на построение линий пересечения поверхностей вращения с пересекающимися осями. В основе этого способа лежит следующее свойство поверхностей вращения: две соосные поверхности вращения пересекаются по окружностям, число которых равно числу точек пересечения их полумеридианов. Эти окружности лежат в плоскостях, перпендикулярных оси поверхностей вращения. У сферы любой диаметр можно принять за ось вращения. Следовательно, сфера с центром на оси поверхности вращения пересекает эту поверхность по одной или нескольким окружностям.

Если ось поверхностей вращения параллельна плоскости проекций, то на эту плоскость линия пересечения проецируется в отрезок прямой линии. На рис. 53 а, б показано пересечение сферы цилиндрической и конической поверхностями вращения, соответственно. На рис. 53 в приведены пересекающиеся соосные цилиндрическая и коническая поверхности вращения.

 

а б в

Рис. 53 Пересечение соосных поверхностей вращения

 

Рассмотрим применение вспомогательных концентрических сфер − сфер с постоянным центром. Этот способ применяют при выполнении следующих условий:

а) пересекающиеся поверхности должны быть поверхностями вращения;

б) оси этих поверхностей должны пересекаться; точку их пересечения принимают за центр вспомогательных сфер;

в) плоскость симметрии поверхностей должна быть параллельна какой-либо плоскости проекций (в противном случае применяют преобразование чертежа).

Рассмотрим построение линии пересечения конических поверхностей вращения (рис. 54). Поверхности и их расположение удовлетворяют приведенным выше условиям.

Прежде чем строить промежуточные точки, необходимо найти опорные точки линии пересечения. Точки А, В, K и L, а также E, F, С и D – это точки, принадлежащие контурам поверхностей. Их можно найти способом концентрических сфер или с помощью плоскостей посредников Σ(Σ₂) и Δ(Δ₁).

Рассмотрим теперь построение промежуточных точек на примере точек 5 и 6. Построения выполняем на фронтальной плоскости проекций. Сфера посредник Θ(Θ₂) с центром в точке О (О ₂) пересекает конические поверхности по окружностям, которые на П ₂ проецируются в отрезки и (проекции двух других окружностей не показаны). Точки 5₂ = 6₂ их пересечения являются фронтальными проекциями точек 5 и 6, которые принадлежат линии пересечения поверхностей, так как принадлежат каждой из этих поверхностей.

Горизонтальные проекции точек 5 и 6 находим из условия принадлежности точки поверхности. В данном случае используется принадлежность точек окружности mⁱ на «вертикальной» конической поверхности. Точки 5₂ и 6₂ находятся по линии проекционной связи на .

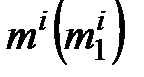Аналогично можно построить любое количество точек искомой линии пересечения. Однако нужно иметь в виду, что не все сферы могут быть использованы для решения задачи.

 

 

Рис. 54 Применение способа вспомогательных концентрических сфер

 

Рассмотрим предельные границы вспомогательных сфер. Радиус сфер посредников изменяется в диапазоне R _max ≥ R ≥ R _min, где R _min – минимальный радиус сферы, R _max – максимальный радиус сферы. Сфера минимального радиуса R _min – это сфера, которая касается одной поверхности и пересекает другую. На рис. 54 такая сфера касается «вертикальной» конической поверхности. С помощью сферы минимального радиуса построены точки 1₂ = 2₂ и 3₂ = 4₂. Горизонтальные проекции точек 1, 2, 3 и 4 построены аналогично точкам 5 и 6.

Радиус максимальной сферы равен расстоянию от точки пересечения осей поверхностей до самой удаленной точки пересечения контурных образующих этих поверхностей. На рис 54 – сфера R _max =[ O ₂ L ₂].

Для установления видимости проекций линии пересечения анализируем расположение точек относительно контуров поверхностей. Так, относительно П ₁, видимым будет участок кривой, расположенный выше контура горизонтальной конической поверхности (вторая поверхность на видимость на П ₁ не влияет). Горизонтальная проекция невидимой части линии показана штриховой линией.

Точки А, В и K, L принадлежат фронтальным контурам поверхностей и отделяют видимую часть линии пересечения от невидимой при проецировании на П ₂. Фронтальные проекции видимой и невидимой частей линии пересечения на рис. 54 совпадают.

 

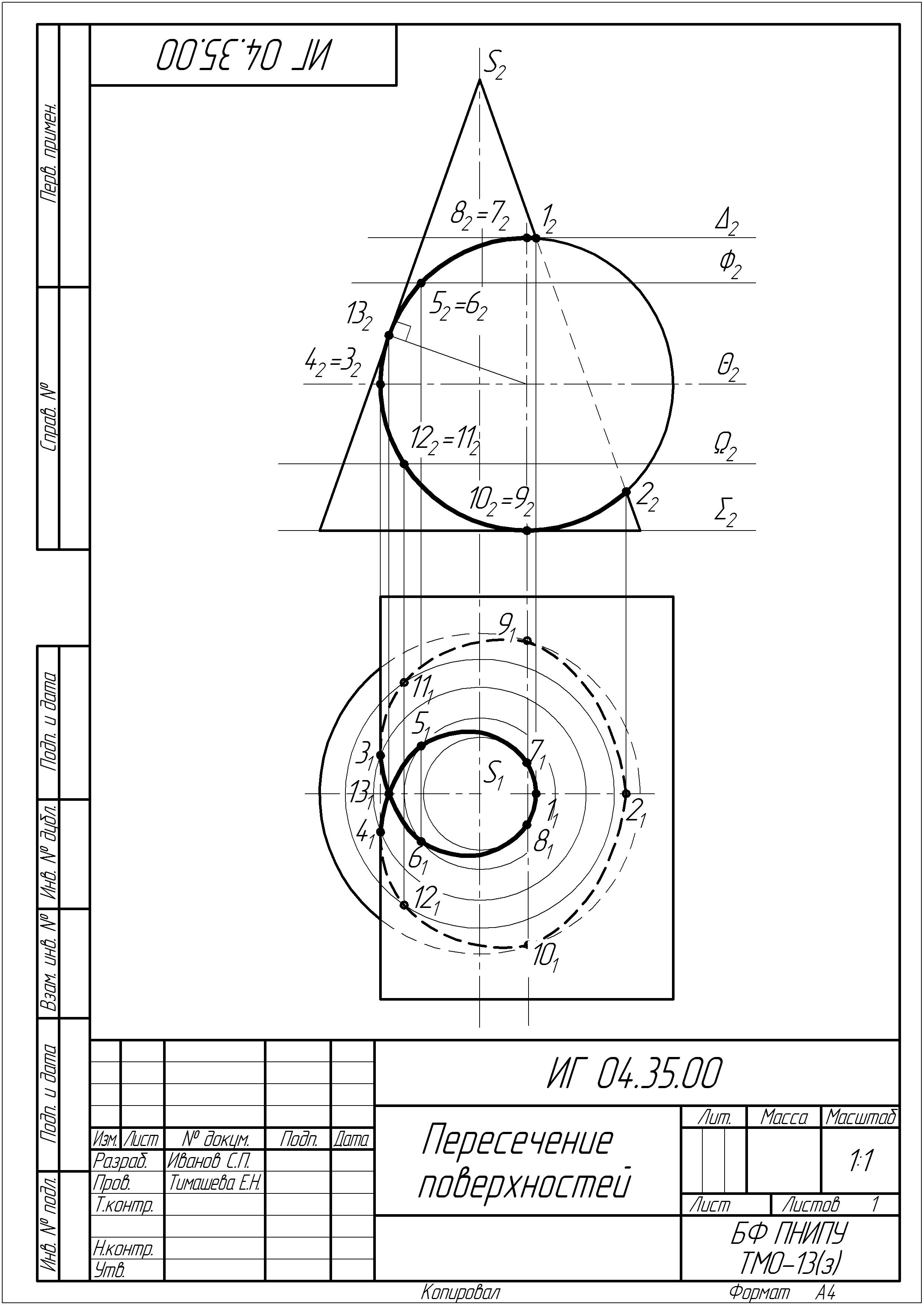
Практическое задание № 5. Выполните чертеж двух пересекающихся поверхностей. Линию их пересечения определите методом вспомогательных плоскостей (формат А4).

Работу выполняют в следующей последовательности (рис. 55):

1) определяют точки пересечения очерковых образующих одной поверхности с другой;

2) определяют наивысшие и наинизшие точки линии пересечения;

3) определяют промежуточные точки линии пересечения с помощью вспомогательных плоскостей;

4) все найденные точки пересечения последовательно соединяют кривой линией, учитывая их видимость.

При выборе вспомогательных секущих плоскостей необходимо помнить, что они должны пересечь одновременно обе поверхности и дать наипростейшие фигуры сечения. Для всех вариантов заданий вспомогательными секущими плоскостями могут быть выбраны плоскости уровня: для одних – горизонтальные, для других – вертикальные или те и другие. Точками пересечения поверхностей являются точки пересечения контуров фигур сечения поверхностей, лежащих в одной и той же вспомогательной секущей плоскости. Каждая секущая плоскость может определить от одной до четырех точек линии пересечения в зависимости от характера пересекающихся поверхностей, их расположения относительно друг друга и положения самой секущей плоскости.

Рис. 55 Образец выполнения практического задания № 5

 

Тема 5

ИЗОБРАЖЕНИЯ: ВИДЫ, РАЗРЕЗЫ, СЕЧЕНИЯ

 

Чертежи выполняют в строгом соответствии с правилами проецирования с соблюдением установленных требований и условностей.

Требования, предъявляемые к чертежу: обратимость, точность, наглядность, простота.

Чертеж называется обратимым, если по изображению фигуры можно восстановить ее форму, размеры и положение в пространстве. Чертеж должен быть наглядным и давать четкое представление об изображаемом предмете. Чертеж должен быть простым для графического исполнения.

Общие требования к содержательной части чертежа установлены ГОСТ 2.109-73.

При выполнении чертежей в электронном виде необходимо руководствоваться ГОСТ 2.051-2006, ГОСТ 2.052-2006, ГОСТ 2.053-2006.

Правила выполнения изображений на чертежах установлены ГОСТ 2.305-2008.

При выполнении графических документов в форме электронных моделей для получения соответствующих изображений следует применять сохраненные виды.

Вид справа

Вид слева

Вид сзади

Вид снизу

Вид спереди - главный

Вид сверху

Изображение предметов на чертеже выполняется по методу прямоугольного проецирования. Изображаемый предмет располагают между наблюдателем и соответствующей плоскостью проекций. За основные плоскости проекций принимают шесть граней куба, совмещаемых с плоскостью чертежа (рис. 56).

Рис. 56 Предмет и его проекции на основных плоскостях

Изображение на фронтальной плоскости проекций принимается на чертеже в качестве главного. Главное изображение выбирают таким образом, чтобы оно давало наиболее полное представление о форме и размерах предмета.

Изображением является любой чертеж. В зависимости от содержания изображения разделяют на виды, разрезы и сечения.

 

Виды

Вид – это изображение обращенной к наблюдателю видимой части поверхности предмета. Для сокращения количества изображений допускается на видах показывать штриховыми линиями невидимые поверхности предмета (см. рис. 56).

Виды разделяют на основные, дополнительные и местные.

Основными называются виды, расположенные на любой из шести основных плоскостей с сохранением проекционной связи между ними. Вид спереди – главный вид; вид сверху – под видом спереди; вид слева – справа от главного; вид справа – слева от главного; вид снизу – над главным видом; вид сзади – справа от вида слева или слева от вида справа (см. рис. 56). Названия видов на чертеже не надписываются.

Если какой-либо вид расположен вне проекционной связи с главным изображением или отделен от него другими изображениями, то стрелкой указывают направление проецирования. Над стрелкой указывают прописную букву кириллицы. Той же буквой обозначают построенный вид (рис. 57).

 

Рис. 57 Основной вид (Б) и дополнительный вид (А)