Сложный (пространственный) изгиб.

Лекция 8.

ПЛАКАТ 1,2

Теории прочности.

Сложное сопротивление.

ПЛАКАТ 3

Объемное напряженное состояние (сложное).

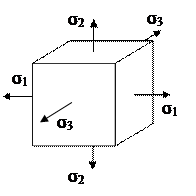При объемном (трехосном) напряженном состоянии все три главных напряжения не равны нулю.

Напряжения по наклонным площадкам, не параллельным ни одному из главных напряжений определяется по формулам:

σ_α= σ₁·cos²α₁+ σ₂·cos²α₂+ σ₃·cos²α₃ (1)

 

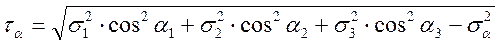(2)

где α₁, α₂, α₃ – углы, которые образует нормаль к рассматриваемой площадке соответственно с направлениями главных напряжений σ₁, σ₂, σ₃.

Максимальное касательное напряжение равно полуразности наибольшего и наименьшего из главных напряжений:

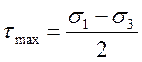(3)

Оно действует по площадке наклоненной под углом 45⁰ к напряжениям σ₁ и σ₃.

Согласно закону Гука, в направлении каждого главного напряжения происходит продольная деформация:

 

ПЛАКАТ 4

а в перпендикулярных направлениях – поперечная деформация:

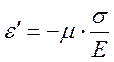
Суммируя деформации по каждому направлению, получаем обобщенный закон Гука для объемного напряженного состояния:

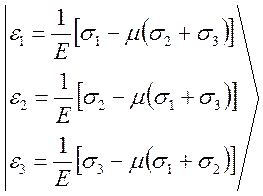(4)

где ε₁, ε₂, ε₃ – деформации в направлении главных напряжений – главные деформации, а μ – коэффициент Пуассона.

Из (4) при σ₃=0 получаем закон Гука при плоском напряженном состоянии, а при σ₂=0 и σ₃=0 – при линейном.

При объемном напряженном состоянии опыт не может дать однозначный ответ на вопрос «Какое из трех главных напряжений, или какое их сочетание вызывает нарушение прочности – разрушение или текучесть».

Поэтому для составления условий прочности приходится прибегать к гипотезам о причинах нарушения прочности.

ПЛАКАТ 5

Понятие о теориях прочности.

Теорией прочности называются теоретические построения, основанные на тех или иных гипотезах о причинах нарушения прочности. Суть применения этих гипотез для оценки прочности материала, заключается в замене фактического напряженного состояния равноопасным (эквивалентным) ему линейным напряженным состоянием.

I теория прочности – теория наибольших нормальных напряжений.

Предполагают, что причиной нарушения прочности является наибольшее из главных напряжений:

σ₁> σ₂> σ₃

σ_max= σ₁≤[σ]

Если [σ]_С≠[σ]_Р, то σ_Рmax≤[σ]_Р и σ_Сmax≤[σ]_С (5)

т.е. наибольшее напряжение не должно превышать допускаемого.

II теория прочности – теория наибольших линейных деформаций.

Предполагают, что причиной нарушения прочности является наибольшая относительная деформация.

ε_max≤[ε] (6)

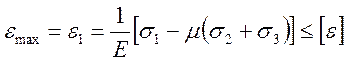
Имея ввиду, что 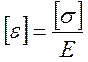, окончательно получаем:

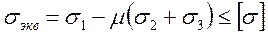(6)¹

т.е. эквивалентное напряжение не должно превышать допускаемого.

ПЛАКАТ 6

III теория прочности – теория наибольших касательных напряжений.

Предполагают, что причиной нарушения прочности является сдвиг, вызванный касательными напряжениями, при этом условие прочности:

τ_max≤[τ] (7)

учитывая формулу (3):

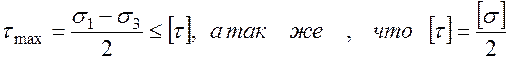
получим:

σ_экв=σ₁ – σ₃≤[σ] (7)¹

Для плоского напряженного состояния:

 

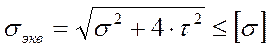(7)¹¹

IV теория прочности – энергетическая теория прочности.

Предполагают, что причиной нарушения прочности является потенциальная энергия упругой деформации, накапливающаяся в единице объема материала. Условие прочности имеет вид:

U≤[U] (8)

Выразив U и [U] через главные напряжения, получим:

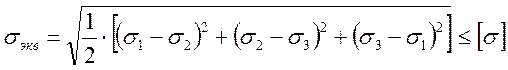(8)¹

Для плоского напряженного состояния:

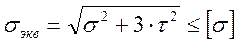
ПЛАКАТ 7

V теория прочности – теория прочности Мора.

Условие прочности:

σ_экв=σ₁ – k·σ₃≤[σ] (9)

где,

В настоящее время, в практических расчетах используют:

для пластичных материалов – III и IV теории прочности;

для хрупких материалов – теорию прочности Мора.

ПЛАКАТ 8

Сложное сопротивление.

Сложным видом сопротивления принято считать такой вид нагружения, при котором в поперечных сечениях стержня действуют два и более внутренних силовых фактора, одновременно учитываемых при расчете на прочность.

Общим случаем сложного сопротивления является случай, когда в сечении действуют все шесть силовых факторов:

N_Z – продольная сила;

Q_X (F_X) – поперечная сила;

Q_Y (F_Y) – поперечная сила;

M_X – изгибающий момент;

M_Y – изгибающий момент;

M_Z (T_K) – крутящий момент.

До сих пор мы рассматривали методы расчета напряжений и перемещений от каждого из этих факторов. При действии нескольких факторов используют принцип суперпозиции (независимости действия сил) для определения суммарного результата.

К наиболее распространенным видам сложного сопротивления относятся сложный изгиб (изгиб в двух плоскостях), изгиб с растяжением и изгиб с кручением.

Порядок решения таких задач следующий:

1. Методом сечений определяют ВСФ и строят их эпюры;

2. По эпюрам определяют опасное сечение;

3. На основании принципа суперпозиции определяют нормальные и касательные напряжения от каждого ВСФ;

4. Исследуя распределение напряжений по сечению, устанавливают опасную точку;

5. Составляют условие прочности для опасной точки.

ПЛАКАТ 9

Сложный (пространственный) изгиб.

x

Если силы, или пары сил – моменты, приложенные к оси стержня, действуют в двух взаимно перпендикулярных главных плоскостях, то изогнутая ось балки представляет, в общем случае, пространственную кривую, поэтому изгиб называется пространственным или сложным.

 

1. Определяем М_И и строим эпюры по плоскостям:

 

М_Х= –F₁·z│ ^l₀; М_Y= F₂·z│ ^l₀

2. Опасное сечение в заделке.

3. ;

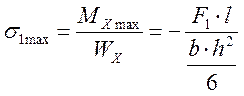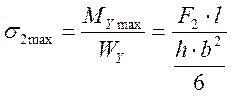
от совместного действия:

σ = ±│ σ₁│±│ σ₂│ (10)

Знак «+» ставится если точки лежат в растянутой зоне, знак «–» - в сжатой.

ПЛАКАТ 10

4. Рассмотрим распределение напряжений по опасному сечению:

(·) А σ_А= σ₁+ σ₂ (·) B σ_B= σ₁- σ₂

(·) C σ_C= - σ₁- σ₂ (·) D σ_D= - σ₁+ σ₂

Наибольшие напряжения в зонах I и III, точки А и С при одинаковых знаках. Условие прочности:

(·) А σ_max= σ_1max+ σ_2max≤[σ]_раст

(·) С σ_max= │- σ_1max- σ_2max │≤[σ]_сжат

 

Перемещения при сложном изгибе (максимальные):

а) плоскость YOZ:

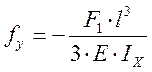
б) плоскость XOZ: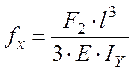

Общее перемещение:

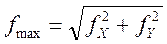(11)

ПЛАКАТ 11

Косой изгиб.

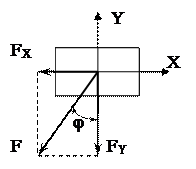
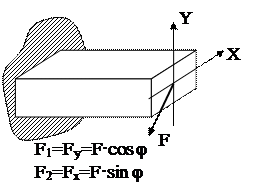Если плоскость действия внешних сил не совпадает ни с одной из главных плоскостей инерции бруса, изгиб называется косым.

Силу раскладывают на две составляющие и рассматривают как сложный изгиб (10) и (11).

ПЛАКАТ 12