Функциональные ряды
Определение. Рассмотрим последовательность функций  , имеющих общую область определения D. Ряд вида
, имеющих общую область определения D. Ряд вида
 , (2.1.1)
, (2.1.1)
называется функциональным.
При каждом частном значении x=x 0 такой ряд превращается в числовой ряд, который может сходиться или расходиться. Множество всех значений аргумента x, при которых функциональный ряд превращается в сходящийся числовой ряд, называется областью сходимости функционального ряда.
Пример 1.
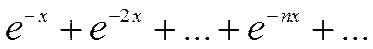
Область определения всех этих функций:  . Все члены ряда >0 Þ ряд знакоположительный. Для нахождения области сходимости применим радикальный признак Коши:
. Все члены ряда >0 Þ ряд знакоположительный. Для нахождения области сходимости применим радикальный признак Коши:

 , т.к. не зависит от п.
, т.к. не зависит от п.
Ряд сходится, если  , т.е.
, т.е.
 ;
;
Ряд расходится, если  , т.е.
, т.е.  ;
;
При х =0 получим числовой ряд 1+1+1+…+…, который расходится.
Таким образом, областью сходимости является промежуток 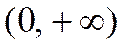 (рис.2.1.1).
(рис.2.1.1).
Например, при х =1 получим числовой ряд  Это геометрическая прогрессия со знаменателем
Это геометрическая прогрессия со знаменателем 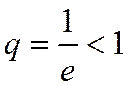 Þ сходится. При х =-1 ряд имеет вид
Þ сходится. При х =-1 ряд имеет вид 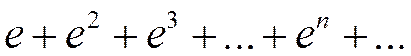 Это прогрессия со знаменателем
Это прогрессия со знаменателем  Þ расходится.
Þ расходится.
 Пример 2.
Пример 2. 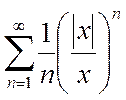 . ООФ:
. ООФ: 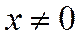 . Раскроем модуль.
. Раскроем модуль.
При 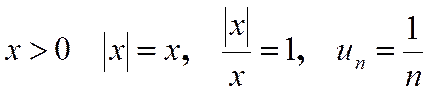 - гармонический ряд, расходится.
- гармонический ряд, расходится.
При  - ряд Лейбница, сходится.
- ряд Лейбница, сходится.
Область сходимости 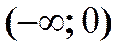 (рис.2.1.2).
(рис.2.1.2).
Частичная сумма функционального ряда

Это функция от х, т.к. при любом х будет своё выражение 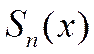 . Последовательность частичных сумм при каждом х будет иметь свой предел, следовательно:
. Последовательность частичных сумм при каждом х будет иметь свой предел, следовательно:
сумма сходящегося функционального ряда является некоторой функцией аргумента x, определённой в области его сходимости. Символическая запись

означает, что S (x) является суммой ряда в области D.
По определению сумма ряда S (x) является пределом последовательности его частичных сумм 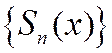 при
при  :
:
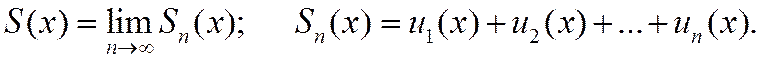 (2.1.2)
(2.1.2)
Для сходящихся рядов справедливо равенство:
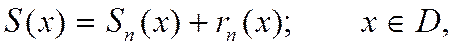 (2.1.3)
(2.1.3)
где  - остаток ряда.
- остаток ряда.
Из выражения (2.1.3) следует равносильность предельных соотношений:
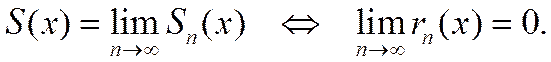 (2.1.4)
(2.1.4)
Степенные ряды. Основные понятия и определения
Частным случаем функциональных рядов являются степенные ряды.
Определение. Степенным рядом называется функциональный ряд вида:
 . (2.2.1)
. (2.2.1)
где 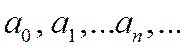 - постоянные, называемые коэффициентами ряда; x 0 - известное число.
- постоянные, называемые коэффициентами ряда; x 0 - известное число.
При  ряд приобретает вид
ряд приобретает вид
 , (2.2.2)
, (2.2.2)
При x=x 0ряд превращается в свой первый коэффициент  . Тогда сумма ряда равна этому числу, и он сходится. Поэтому точка x=x 0называется центром сходимости степенного ряда (2.2.1). Таким образом, степенной ряд всегда сходится хотя бы в одной точке. Сделав замену x-x 0 =Х, можно свести общий случай степенного ряда (2.2.1) к частному случаю (2.2.2). В дальнейшем мы будем в основном рассматривать ряды типа (2.2.2). Этот ряд всегда сходится по крайней мере в точке х =0.
. Тогда сумма ряда равна этому числу, и он сходится. Поэтому точка x=x 0называется центром сходимости степенного ряда (2.2.1). Таким образом, степенной ряд всегда сходится хотя бы в одной точке. Сделав замену x-x 0 =Х, можно свести общий случай степенного ряда (2.2.1) к частному случаю (2.2.2). В дальнейшем мы будем в основном рассматривать ряды типа (2.2.2). Этот ряд всегда сходится по крайней мере в точке х =0.
Придавая х различные числовые значения, будем получать различные числовые ряды, которые могут оказаться сходящимися или расходящимися. Множество значений х, при которых степенной ряд сходится, называется областью сходимости этого ряда.
Очевидно, что частичная сумма степенного ряда
 (2.2.3)
(2.2.3)
является функцией переменной х. Поэтому и сумма ряда 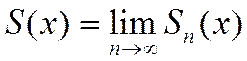 является некоторой функцией переменной х, определенной в области сходимости ряда:
является некоторой функцией переменной х, определенной в области сходимости ряда:
 . (2.2.4)
. (2.2.4)
Теорема Абеля
Исследование сходимости функциональных рядов при заданном значении х можно производить при помощи известных признаков сходимости числовых рядов. Характер же сходимости именно степенных рядов определяется следующей основной теоремой.
Теорема Абеля.
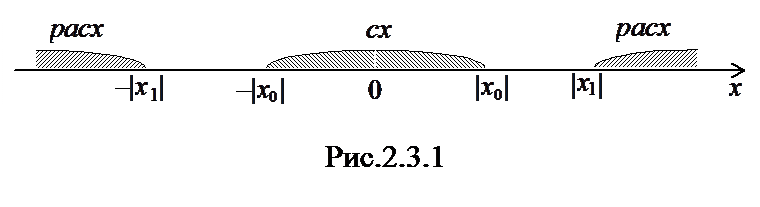 |
1) Если степенной ряд (2.2.2) сходится при x=x 0 ¹ 0, то он сходится, причем абсолютно, при любом значении x, удовлетворяющем условию
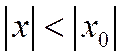 , т.е. в интервале
, т.е. в интервале 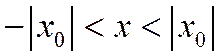 .
.
2) Если ряд (2.2.2) расходится при x=x 1, то он расходится и при всех x, удовлетворяющих условию  (рис.2.3.1).
(рис.2.3.1).
Точки, в которых степенной ряд сходится, называются точками сходимости, а где он расходится – точками расходимости.
 | |||
 |
Радиус сходимости и интервал сходимости
Степенного ряда
Используя теорему Абеля, можно показать, что для каждого степенного ряда вида (2.2.2), имеющего как точки сходимости, так и точки расходимости (т.е. сходящегося не только в точке 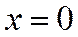 и не на всей числовой прямой), существует такое положительное число R, что для всех x, удовлетворяющих условию
и не на всей числовой прямой), существует такое положительное число R, что для всех x, удовлетворяющих условию 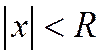 , ряд абсолютно сходится; а при
, ряд абсолютно сходится; а при  ряд расходится. При x =± R возможны различные случаи: а) ряд может сходиться в обеих точках ± R; б) ряд может расходиться в обеих точках ± R; в) ряд может сходиться в одной из них абсолютно или условно и расходиться в другой (рис.2.4.1). Чтобы выяснить сходимость ряда на границах интервала, нужно подставить значения x =± R в ряд (2.2.2) и исследовать полученные числовые ряды:
ряд расходится. При x =± R возможны различные случаи: а) ряд может сходиться в обеих точках ± R; б) ряд может расходиться в обеих точках ± R; в) ряд может сходиться в одной из них абсолютно или условно и расходиться в другой (рис.2.4.1). Чтобы выяснить сходимость ряда на границах интервала, нужно подставить значения x =± R в ряд (2.2.2) и исследовать полученные числовые ряды:
 |
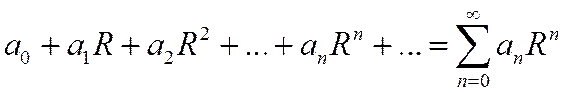
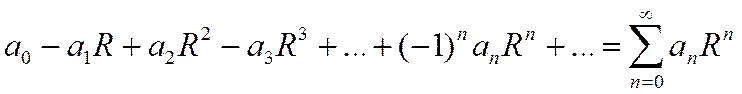
с помощью известных признаков сходимости. В одних случаях могут получаться знакоположительные ряды, в других – знакочередующиеся.
Число R называют радиусом сходимости степенного ряда, а интервал  - интервалом сходимости. После исследования границ получим уточнённый интервал сходимости, называемый областью сходимости.
- интервалом сходимости. После исследования границ получим уточнённый интервал сходимости, называемый областью сходимости.
Предельные случаи, когда ряд (2.2.2) сходится только при x =0 или сходится при всех значениях x, символически записывают так: R =0 или R =¥.
Так как внутри интервала сходимости степенной ряд сходится абсолютно, то для нахождения интервала сходимости этого ряда достаточно найти те значения аргумента x, при которых сходится ряд, составленный из модулей членов степенного (в общем случае знакопеременного) ряда. Для этого можно применить признак Д’Аламбера. Это равносильно тому, чтобы к исходному ряду применить общий признак Д’Аламбера.
Пример 1. Найти интервал сходимости ряда

По общему признаку Д’Аламбера вычисляем предел модуля отношения последующего члена к предыдущему:
 Þ ряд абсолютно сходится, если
Þ ряд абсолютно сходится, если 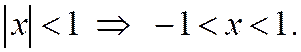 Длина интервала сходимости равна двум единицам, радиус сходимости
Длина интервала сходимости равна двум единицам, радиус сходимости  . Проверим сходимость ряда при x =-1 и x =1. При x =-1:
. Проверим сходимость ряда при x =-1 и x =1. При x =-1:
 .
.
Полученный числовой ряд сходится абсолютно, т.к. ряд, составленный из модулей его членов (он находится в скобках), является обобщённым гармоническим с 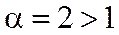 . При x =1:
. При x =1:
 ряд сходится абсолютно по той же причине.
ряд сходится абсолютно по той же причине.
 |
Итак, областью сходимости ряда является промежуток -1£ x £1, или
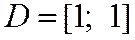 .
.
Замечание. Радиус сходимости ряда с последовательно возрастающими степенями (нулевая, первая, вторая, и.т.д) можно также найти по формуле:
 , (2.4.1)
, (2.4.1)
где  и
и 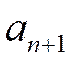 – коэффициенты при степенях х. Подчеркнём, что она годится лишь в случае, когда в ряде вида (2.2.2) или (2.2.1) присутствуют все степени х.
– коэффициенты при степенях х. Подчеркнём, что она годится лишь в случае, когда в ряде вида (2.2.2) или (2.2.1) присутствуют все степени х.
В данном примере
 .
.
Центр сходимости  .
.
Пример 2. Найти интервал сходимости степенного ряда  .
.
Данный ряд имеет вид (2.2.1): 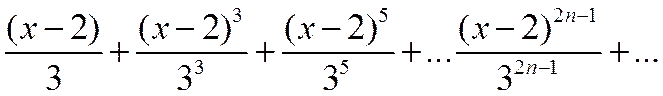
Все степени х и 3 нечётны. Воспользуемся общим признаком Д’Аламбера.
 ,
,
 .
.
По признаку Д’Аламбера ряд будет сходиться тогда, когда l <1, т. е. при 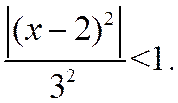 Решая это неравенство относительно x, получим:
Решая это неравенство относительно x, получим:

 Û
Û 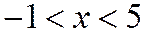 .
.
Интервал сходимости (без учёта границ)  , его длина равна 6 единицам. Радиус сходимости
, его длина равна 6 единицам. Радиус сходимости  , центр сходимости
, центр сходимости  .
.
Проверим границы интервала сходимости. Для этого надо исследовать сходимость двух числовых рядов, полученных подстановкой в степенной ряд граничных точек интервала. В данном примере такими точками являются x 1=-1 и x 2=5.
При x 1=-1:
 |
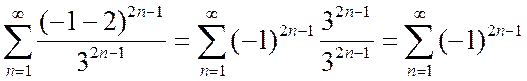
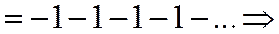
Þ общий член ряда 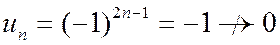 при
при  , следовательно, ряд расходится.
, следовательно, ряд расходится.
При x 2=5:  при
при 
Þ ряд расходится. Итак, областью сходимости заданного ряда является открытый интервал -1< x <5, или  (рис.2.4.3).
(рис.2.4.3).
Пример 3. Найти интервал сходимости ряда  .
.
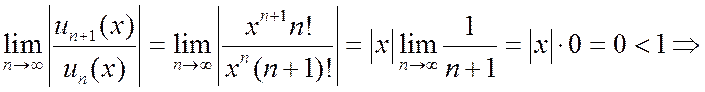
Þ согласно общему признаку Д’Аламбера ряд сходится абсолютно при любых значениях x;  , R =¥.
, R =¥.
Пример 4. 

 .
.