Критерий разложимости функции в ряд Тейлора
Вернемся к рядам. В §2.7 мы установили, что если функцию 
можно разложить в сходящийся к ней степенной ряд, то он является для этой функции рядом Тейлора.
Возникает вопрос, справедливо ли обратное утверждение? Пусть функция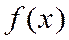 
бесконечно дифференцируема на интервале 
. Мы можем формально построить для нее ряд Тейлора. Но пока мы не знаем, будет ли наша функция суммой этого ряда, т.е. будет ли построенный ряд Тейлора сходиться к нашей функции на интервале , вместо знака равенства поставим знак соответствия:
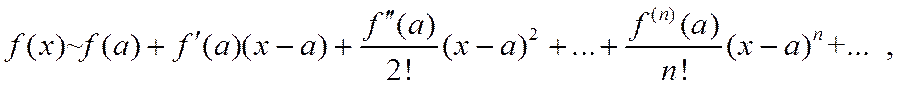
Выясним, при каких условиях этот знак можно заменить на знак равенства. Напишем формулу Тейлора для функции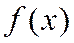 
:
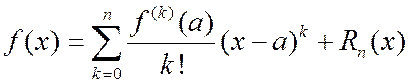, (2.9.1)
где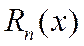 
- остаточный член, а
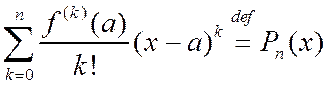. (2.9.2)
– многочлен Тейлора n -ой степени, который можно рассматривать как частичную сумму ряда Тейлора. Таким образом,
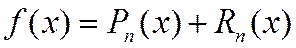. (2.9.3)
Остаточный член формулы Тейлора для функции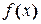 
можно определить как разность между функцией 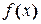и частичной суммой ряда Тейлора:
. (2.9.4)
При увеличении номера п число слагаемых в частичной сумме, т.е. в многочлене Тейлора, увеличивается, а остаточный член изменяется. Можно рассмотреть последовательность остаточных членов 
. Это последовательность функций, определенных в той же окрестности точки а, в которой имеет место бесконечная дифференцируемость функции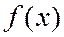 
. Остаточный член показывает погрешность, получающуюся при замене функции частичной суммой ряда Тейлора. Ясно, что для получения хорошего приближения 
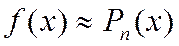последовательность остаточных членов 
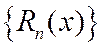должна стремиться к нулю. Вместо сочетания «последовательность остаточных членов» часто говорят просто «остаточный член».
Теорема 1 О необходимом и достаточном условии сходимости ряда Тейлора к функции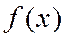 
.
Для того чтобы функцию 
можно было разложить в ряд Тейлора
(2.9.5)
на интервале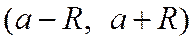 
, необходимо и достаточно, чтобы 
имела на этом интервале производные любого порядка и чтобы остаточный член 
в данной формуле Тейлора (2.9.1) стремился к нулю при всех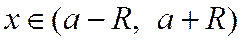 
, когда n ®¥.
Теорема 2 О достаточном условии сходимости остаточного члена формулы Тейлора к нулю.
Если функция в e-окрестности точки а имеет производные любого порядка, ограниченные одним и тем же числом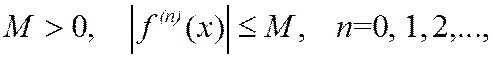 
то остаточный член ее формулы Тейлора в этой окрестности стремится к нулю при 
:
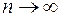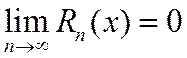. (2.9.8)
Разложение элементарных функций в ряд Маклорена
1. 
.
 |
В примере 2 была выведена формула Маклорена для этой функции. Можно показать, что остаточный член стремится к нулю при
.
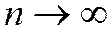Согласно теореме о необходимом и достаточном условии сходимости ряда Тейлора к функции 
полученный ряд сходится к функции 
и можно написать равенство:
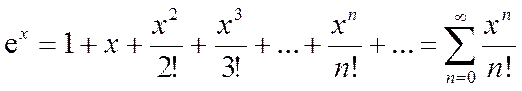. (1*)
Найдем интервал сходимости этого ряда. По общему признаку Д’Аламбера
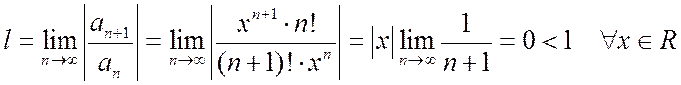Þ
ряд Маклорена сходится на всей числовой оси, т.е. для всех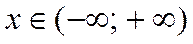 
.
Заменим х на (- х):
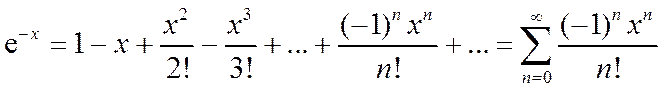
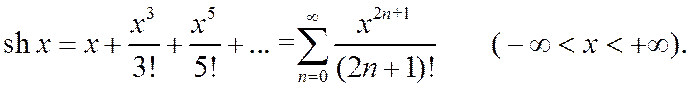2. 
(2*)
(нечетные степени с факториалами, все с плюсами)
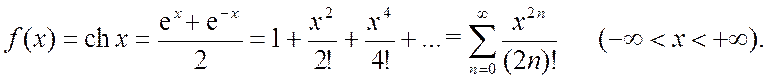3. 
(3*)
(четные степени с факториалами, все с плюсами). Разложение (3*) можно также получить с помощью почленного дифференцирования ряда (2*).
4. Найдём сумму бесконечно убывающей геометрической прогрессии со знаменателем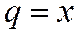 
, 
:
.
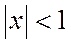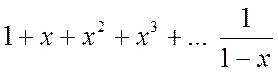Переписав это равенство справа налево, получим разложение в ряд функции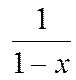 
:
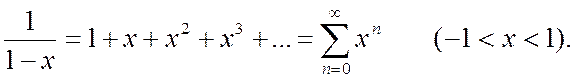(4*)
5. В разложении (4*) выполним замену х на (- х). Тогда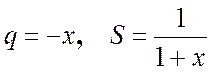 
:
(5*)
6. Проинтегрируем ряд (5*) почленно от 0 до переменного предела х:
.
Получили разложение натурального логарифма:
(6*)
(без факториалов). Интервал сходимости по теореме об интегрировании степенных рядов остался прежним. Исследуем сходимость ряда на концах интервала. При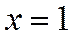 
получим знакопеременный гармонический ряд 7°, сходящийся по теореме Лейбница:
.
При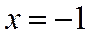 
получаем 
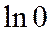и расходящийся гармонический ряд. Таким образом, интервал сходимости ряда (6*) 
.
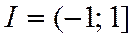7. В разложении (5*) заменим х на (х 2):
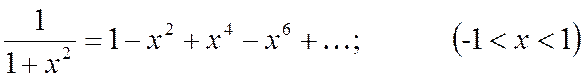
Проинтегрируем почленно этот ряд:
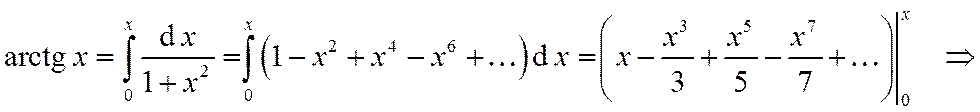
. (7*)
(нечетные степени без факториалов). При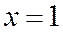 
получим сходящийся по Лейбницу ряд (8°):
.
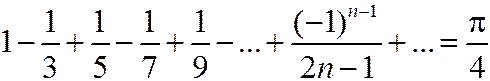При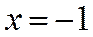 
- тот же ряд, но с противоположными знаками:
.
Таким образом, интервал сходимости ряда (7*) 
.
8.
 |
, 
,
, 
,
, 
,
, 
,
, 
,
……………………………………………………….
, 
.
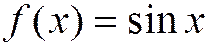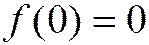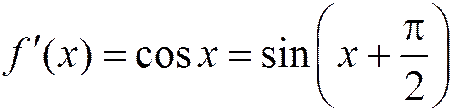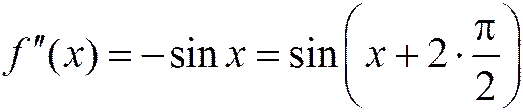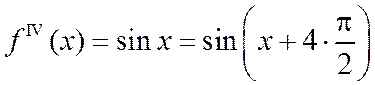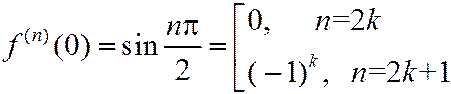Взятие производной – это поворот на 90° (нрис.2.10.3). Производные любого порядка ограничены: на 
: 
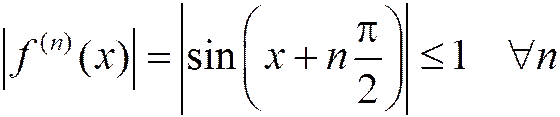. Поэтому по теореме 2 
, и функция 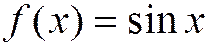разлагается в сходящийся к ней на ряд Маклорена по степеням x:
(8*)
Покажем, что полученный ряд сходится на всей числовой оси. По общему признаку Д’Аламбера:
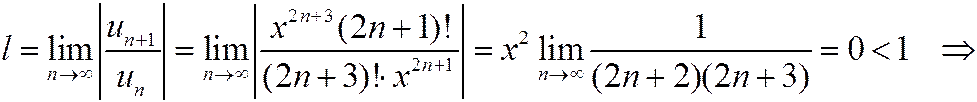сходится при всех х.
Ряд (8*) отличается от разложения гиперболического синуса (2*) знакопеременностью.
9. 
.
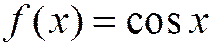Почленным дифференцированием ряда (8*) получаем разложение косинуса в ряд Маклорена:
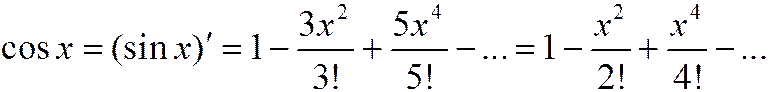
Таким образом,
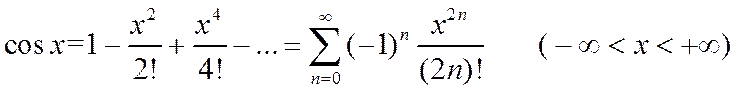(9*)
Т.к. ряд (9*) получен путем дифференцирования ряда (8*), то по теореме о дифференцировании степенных рядов ряд (9*) имеет тот же интервал сходимости, что и ряд (8*).
Ряд (9*) отличается от разложения гиперболического косинуса (3*) знакопеременностью.