Лекция 2-8
Интегралы
Интегралы. Вычисление площади под графиком
Определение первообразной
Определение. Первообразной для непрерывной на интервале 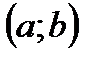 функции
функции 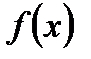 на этом интервале называется функция
на этом интервале называется функция 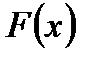 , для которой
, для которой 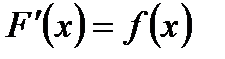 .
.
Аналогично определяется первообразная для функции 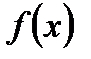 на отрезке
на отрезке  . Под производной в точке a надо понимать правую производную, а в точке b – левую.
. Под производной в точке a надо понимать правую производную, а в точке b – левую.
Для каждой 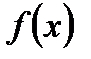 существует не одна, а целый класс первообразных: если функция
существует не одна, а целый класс первообразных: если функция 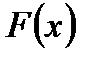 является первообразной для
является первообразной для 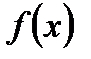 на интервале
на интервале 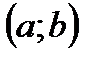 , то всевозможные функции вида
, то всевозможные функции вида 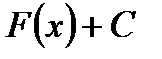 , где С – любое число, также являются ее первообразными на этом интервале.
, где С – любое число, также являются ее первообразными на этом интервале.

Определение. Неопределенным интегралом от непрерывной на интервале 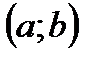 функции
функции 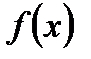 называют любую ее первообразную.
называют любую ее первообразную.
Обозначение: 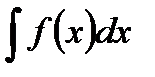 , где
, где  – подинтегральная функция, а
– подинтегральная функция, а  – подинтегральное выражение.
– подинтегральное выражение.
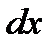 показывает, по какой переменной берется интеграл / было произведено дифференцирование.
показывает, по какой переменной берется интеграл / было произведено дифференцирование.


Пример 1

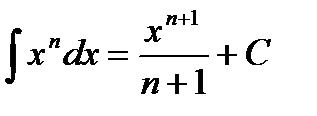
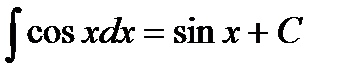
Первообразные элементарных функций

Правила вычисления неопределенных интегралов
· 
· 
· 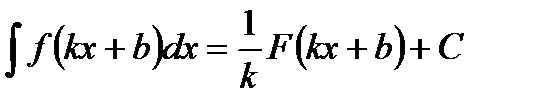
Пример 2
Найти 
Замена переменной
Если 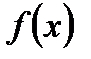 непрерывна, то можно сделать замену
непрерывна, то можно сделать замену  , где
, где  непрерывна вместе со своей производной
непрерывна вместе со своей производной 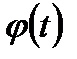 :
: 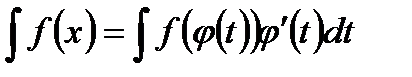
Пример 3. 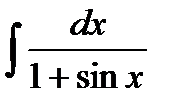
Пример 4. 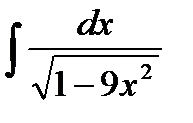
Интегрирование по частям
Если  и
и 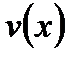 - некоторые дифференцируемые функции, то
- некоторые дифференцируемые функции, то 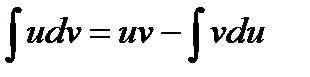
Пример 5.

Пусть  ,
, 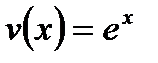 . Тогда:
. Тогда:
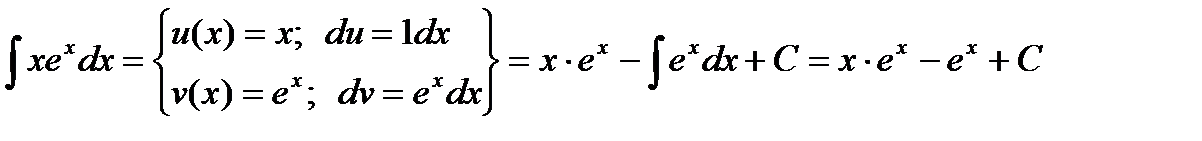
Алгебраические преобразования
Пример 6. Разложение на простейшие дроби
Определение. Простейшими дробями называются дроби вида  ,
, 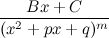 , где
, где  ,
, 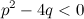
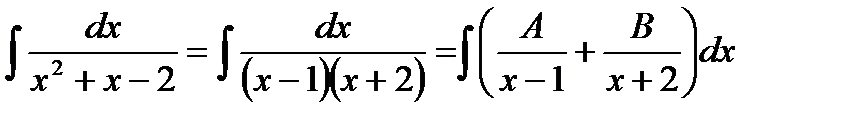



Площадь криволинейной трапеции
Определения. Криволинейной трапецией называется фигура, ограниченная кривой – графиком функции  , осью Ох и прямыми x=a, x=b.
, осью Ох и прямыми x=a, x=b.
Для решения задачи нахождения площади такой фигуры необходимо разбить отрезок 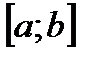 точками
точками 
Площадью криволинейной трапеции называется предел  , где
, где  ,
, 
Сумму  называют интегральной суммой.
называют интегральной суммой.
Определенный интеграл
Определение. Определенным интегралом от функции  на отрезке
на отрезке 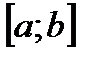 называется предел интегральной суммы, когда длина максимального отрезка разбиения стремится к нулю.
называется предел интегральной суммы, когда длина максимального отрезка разбиения стремится к нулю.
Обозначение: 
Геометрический смысл определенного интеграла: он равен ориентированной площади криволинейной трапеции, ограниченной графиком функции  , осью Ох и прямыми x=a, x=b.
, осью Ох и прямыми x=a, x=b.
Ориентированная площадь в отличие от обычной имеет знак: для фигур выше Ох она положительна, для фигур ниже нее – отрицательна.
! Если в задаче сказано найти площадь, то имеется в виду площадь в обычном понимании, т.е. неотрицательная величина.
Пример 7. Вычислить 
Пример 8. Вычислить площадь закрашенной фигуры

Свойства определенного интеграла
· 
· 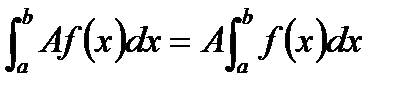
· 
· 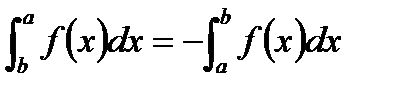
Формула Ньютона-Лейбница
Теорема. Пусть функция  непрерывна на отрезке
непрерывна на отрезке 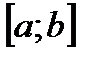 и пусть
и пусть 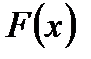 - какая-либо ее первообразная. Тогда справедливо равенство:
- какая-либо ее первообразная. Тогда справедливо равенство: 
Пример 9. Вычислить  . Вычислить площадь закрашенной фигуры. Объяснить полученные результаты
. Вычислить площадь закрашенной фигуры. Объяснить полученные результаты
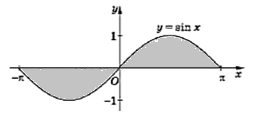
Пример 10. Вывести формулу площади единичного круга
Формула для вычисления объема тела вращения
Если кривая – график непрерывной неотрицательной функции  на отрезке
на отрезке 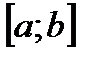 – вращается вокруг оси Ох, то тело, ограниченное поверхностью вращения и плоскостями x=a, x=b, имеет объем
– вращается вокруг оси Ох, то тело, ограниченное поверхностью вращения и плоскостями x=a, x=b, имеет объем

Пример 11. Вывести формулу объема шара 
| Воображариум |
Семинар 2-8
Марта 2019
1. Найти первообразную для функции: 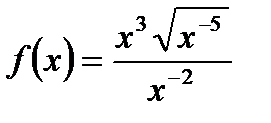
2. Найдите неопределенный интеграл: 
3. Найдите неопределенный интеграл: 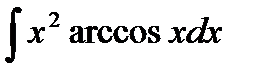
4. Вычислите площадь фигуры, ограниченной линиями  и
и 
5. С помощью вычисления определенного интеграла вывести формулу площади для эллипса с осями a и b.
Домашнее задание 2-8
1. 
2. 
3. 
4. 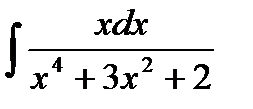
5. 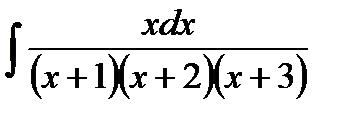
6. 
7. С помощью вычисления определенного интеграла вывести формулу площади для круга радиуса R.
8. Пользуясь геометрическим смыслом определенного интеграла, вычислить:

9. Вычислите площадь фигуры, ограниченной линией 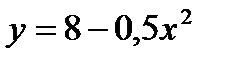 , касательной к ней
, касательной к ней  и прямыми х=0 и х=-3
и прямыми х=0 и х=-3
10. Вычислите площадь фигуры, ограниченной линиями 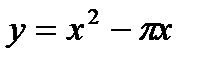 и
и