Определение второй производной, ее физический и
Геометрический смысл.
. Вторая производная – это производная от первой производной:
Стандартные обозначения второй производной:, или (дробь читается так: «два игрек по дэ икс квадрат»). Чаще всего вторую производную обозначают первыми двумя вариантами. Но третий вариант тоже встречается, причем, его очень любят включать в условия контрольных заданий, например: «Найдите функции…».
Рассмотрим простейший пример. Найдем вторую производную от функции.
Для того чтобы найти вторую производную, как многие догадались, нужно сначала найти первую производную:
Теперь находим вторую производную:
Рассмотрим более
Пример 11

Найдем первую производную:
На каждом шаге всегда смотрим, нельзя ли что-нибудь упростить? Сейчас нам предстоит дифференцировать произведение двух функций, и мы избавимся от этой неприятности, применив известную тригонометрическую формулу. Точнее говоря, использовать формулу будем в обратном направлении::
Находим вторую производную:
Готово.
Можно было пойти другим путём – понизить степень функции еще перед дифференцированием, используя формулу:
Если интересно, возьмите первую и вторую производные снова. Результаты, естественно, совпадут.
Отмечу, что понижение степени бывает очень выгодно при нахождении частных производных функции. Здесь же оба способа решения будут примерно одинаковой длины и сложности.
Как и для первой производной, можно рассмотреть задачу нахождения второй производной в точке.
Например: Вычислим значение найденной второй производной в точке:
Необходимость находить вторую производную и вторую производную в точке возникает при исследовании графика функции на выпуклость/вогнутость и перегибы
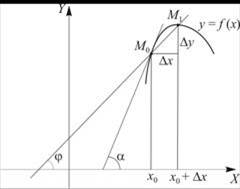
Рисунок 6 – Касательная прямая в М0 к графику функции есть предельное положение секущей М0 М1 При
Геометрический смысл производной:.
Точке М0 отвечает пара чисел, где. Изменим значение Х0, т. е. дадим ему приращение DХ и, таким образом, от точки Х0 на оси абсцисс перейдем в точку Х0 + DХ. Вследствие этого точка М0 на графике передвинется в точку М1. Изменение функции в результате этого перехода обозначим. Отношение показывает, как быстро изменяется функция с изменением Х. Предел этого отношения при называется производной функции в точке Х0.
Def: Производной функции У по аргументу Х называется предел отношения приращения функции DУ к приращению аргумента DХ, вычисленный в процессе, когда приращение аргумента стремится к нулю.
На рис.6 прямая линия, соединяющая две соседние точки М0 и М1, будет секущей для графика. Она наклонена к оси ОХ под углом j, и.
Если DХ устремим к нулю, то точка М1 начнет передвигаться по графику к точке М0, а секущая М0М1 поворачиваться относительно точки М0.
В пределе, при слиянии движущейся точки М1 с неподвижной М0 секущая займет положение касательной. Угол наклона касательной к оси ОХ равен. Таким образом,
Отсюда следует геометрический смысл производной:
Производная функции в точке равна тангенсу угла наклона касательной к графику функции в этой точке:.
Задание Материальная точка движется прямолинейно по закону В какой момент времени (в секундах) ее скорость будет равна 3 м/с?
Решение.Найдем скорость движения рассматриваемой материальной точки, согласно физическому смыслу производной, она равна производной от пути, то есть
По условию известно, что в некоторый момент времени скорость равна 3 м/с, то есть:
Решим полученное уравнение относительно
Ответ 8 cек.
 |
Следовательно, геометрический смысл производной состоит в том, что значение производной в точке касания равно тангенсу угла наклона касательной проведенной к графику функции в эту точку.