Лабораторная работа 4.12
Сложение взаимно перпендикулярных колебаний. Фигуры Лиссажу
Красноухова В.Н. к.ф.-м.н.доц. кафедры кафедры физики и методики обучения физике ОмГПУ(г. Омск)
Цель работы: изучить сложение взаимно перпендикулярных колебаний Оборудование: виртуальная лабораторная работа 4.12. Сложение взаимно перпендикулярных колебаний. Фигуры Лиссажу
https://mediadidaktika.ru/mod/page/view.php?id=96
Указания к теоретической подготовке
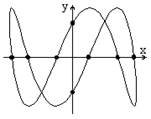 Рис. 2. Пример фигуры Лиссажу Рис. 2. Пример фигуры Лиссажу
|
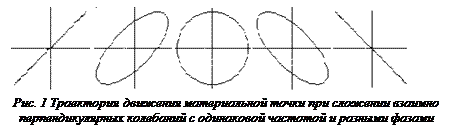 При сложении взаимно перпендикулярных колебаний одинаковой частоты траекторией движения точки, участвующей в этих колебаниях, является эллипс, в некоторых частных случаях вырождающийся в прямую линию (рис.1). В общем случае при сложении взаимно перпендикулярных колебаний разных частот материальная точка описывает сложные кривые. При отношении частот, равном отношению небольших целых чисел 1:1, 1:2, 2:1, 3:2 и т.д., траектории имеют сравнительно простую форму (фигуры Лиссажу) и могут быть получены на экране осциллографа.
При сложении взаимно перпендикулярных колебаний одинаковой частоты траекторией движения точки, участвующей в этих колебаниях, является эллипс, в некоторых частных случаях вырождающийся в прямую линию (рис.1). В общем случае при сложении взаимно перпендикулярных колебаний разных частот материальная точка описывает сложные кривые. При отношении частот, равном отношению небольших целых чисел 1:1, 1:2, 2:1, 3:2 и т.д., траектории имеют сравнительно простую форму (фигуры Лиссажу) и могут быть получены на экране осциллографа.
Если отношение периодов представляет собой рациональное число, то через промежуток времени, равный наименьшему кратному обоих периодов, движущаяся точка снова возвращается в исходное положение, совпадающим с исходным вектором скорости точки, в результате получаются замкнутые траектории. Если отношение периодов иррациональное число, то порождаются незамкнутые траектории.
Число точек пересечения фигуры Лиссажу nX с осью координат ОХ и nу с осью координат ОУ зависит от соотношения частот nX и nу складываемых колебаний. Поэтому по виду фигуры на экране осциллографа можно определить одну из частот, если другая частота известна, используя формулу:
|
|
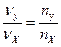 (1)
(1)
Например, на рис. 8.2 число пересечений фигуры с осями равно: nX = 6 и nу = 2, следовательно, 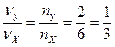 .
.
Описание установки и метода измерения

Виртуальная установка представлена на рис.3. Имеется виртуальный осциллограф, на котором отображается траектория движения колеблющейся частицы. Можно задавать частоты складываемых колебаний и разность их фаз. В правой нижней части расположен секундомер. При нажатии на кнопку «пуск» частица начнёт двигаться по некоторой траектории, которая отображается на экране. Вид траектории зависит от заданных параметров. При нажатии на кнопку «сброс» показания секундомера обнуляются и траектория движения частицы исчезает с экрана осциллографа.
Задание 1. Изучение сложения взаимно перпендикулярных колебаний одинаковой частоты при различных разностях фаз
1. Установите одинаковые частоты w01 и w02. Занесите их значения в таблицу 1.
2. Пронаблюдайте траектории движения частицы при разностях фаз Dj=0; 0,78; 1,57; 2,35; 3,14.
3. Нарисуйте траектории движения частицы при указанных условиях в таблице 1.
4. Получите траектории движения частиц теоретически для разностей фаз Dj=0; 1,57 (или p/2); 3,14 (или p). Считайте, что колебания по оси 0х происходят по закону 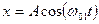 , а по оси 0у по закону
, а по оси 0у по закону 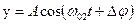 .
.
5. Сравните полученные траектории с наблюдаемыми на экране виртуального осциллографа при тех же условиях. Сделайте вывод.
Таблица 1
| w01, рад/с | w02, рад/с | Dj, рад | Изображение фигуры Лиссажу |
| 0,78 (π/4) | |||
| 1,57(π/2) | |||
| 2,35 (3π/4) | |||
| 3,14 (π) |
6. Установите одинаковые частоты w01=1 рад/с и w02=1 рад/с и Dj=1,57 рад. Определите по секундомеру время одного полного оборота частицы Т. Для этого нужно сделать скриншот экрана (нажать кнопку клавиатуры PrScr (копия экрана)).
|
|
7. Опыт повторите не менее 5 раз, результаты измерения времени занесите в таблицу 2.
8. Рассчитайте период теоретически и сравните с измеренным значением.
Таблица 2
| № | Тi,с | Тср,с | DТi,с | DТ2 i, с2 | S, с | a= К= | DТсл,с | e, % | Т теор, с |
| 1. | |||||||||
| 2. | |||||||||
| 3. | |||||||||
| 4. | |||||||||
| 5. |
Задание 2. Изучение сложения взаимно перпендикулярных колебаний кратных частот при разных разностях фаз
1. Установите кратные частоты w01 и w02. Занесите их значения в таблицу 3.
2. Зарисуйте фигуры Лиссажу в таблицу 3 при соотношениях частот 1:2 и 1:3 и Dj=0; 1,57 (или p/2); 3,14 (или p).
Таблица 3
| w01, рад/с | w02, рад/с | Dj, рад | Изображение фигуры Лиссажу |
| 1,57 | |||
| 3,14 | |||
| 1,57 | |||
| 3,14 |
3. Установите не кратные частоты w01 и w02. Пронаблюдайте траекторию движения частицы при любом выбранном Dj. Будут ли эти траектории замкнутыми линиями? Сделайте вывод.
Контрольные вопросы:
1. Запишите уравнение гармонического колебания и поясните смысл входящих в него величин.
2. Как движется материальная точка, если складываются два взаимно перпендикулярных колебания одинаковой частоты, а разность фаз равна 0, p/2, p?
3. Как движется материальная точка, если она одновременно участвует в двух взаимно перпендикулярных колебаниях разных частот? В каком случае получаются фигуры Лиссажу?
|
|
4. Как можно определить отношение частот складываемых колебаний по фигурам Лиссажу?
5. В каком случае результатом сложения двух взаимно перпендикулярных колебаний одинаковой частоты будет наблюдаться эллипс?
Литература:
1. Архангельский М. М. Курс физики. Механика. – М.: Просвещение, 1975. – 424 с.
2. Александров Н. В., Яшкин А. Я. Курс общей физики. Механика. – М.: Просвещение, 1978. – 416 с.
3. Александров В. Н. и др. Лабораторный практикум по общей и экспериментальной физике / под ред. Е. М. Гершензона и А. Н. Мансурова. – М.: Академия, 2004. – 464 с.
4. Бобров П.П. Основные понятия механики: учебное пособие.– Омск: Изд-во ОмГПУ, 2013.- 180 с.
5. Механика. Часть 1. Механика материальной точки: лабораторный практикум / авт.-сост.: Т.А. Беляева, П.П. Бобров, В.Н. Красноухова. – Омск: Изд-во ОмГПУ, 2016. – 52 с.
6. Общая физика: руководство по лабораторному практикуму: учеб. пособие для студ. вузов / под ред.: И. Б. Крынецкого, Б. А. Струкова. - М.: ИНФРА-М, 2008. - 598 с.
Начальные данные по вариантам к заданию 1
| Группа | w01, рад/с | w02, рад/с |