| ln x = 2 - x. | (3.10) |
В виде (3.1) его можно записать либо
| ln x - 2 + x = 0, | (3.11) |
либо
| 2 - ln x - x = 0, | (3.12) |
Оба уравнения приведем к виду (3.8) прибавлением x к правой и левой частям.
Уравнение (3.11) преобразуется к виду:
| x = ln x - 2 + 2 x, | (3.13) |
т.е. 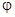 (x)= ln x - 2 + 2 x.
(x)= ln x - 2 + 2 x.
Продифференцируем функцию 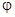 (x):
(x):  (x)=
(x)=  + 2. Не трудно определить, что условие сходимости метода выполняется при -1 < x < -1/3. Но на этапе отделения корней можно убедиться, что корень уравнения лежит в интервале (1,2), и вообще вся функция
+ 2. Не трудно определить, что условие сходимости метода выполняется при -1 < x < -1/3. Но на этапе отделения корней можно убедиться, что корень уравнения лежит в интервале (1,2), и вообще вся функция  (x) из-за наличия логарифмаопределена лишь при x > 0. Это значит, что исходное уравнение преобразованием к виду (3.13) решить методом простых итераций невозможно.
(x) из-за наличия логарифмаопределена лишь при x > 0. Это значит, что исходное уравнение преобразованием к виду (3.13) решить методом простых итераций невозможно.
Уравнение (3.12) преобразуется к виду:
| x = 2 - ln x, | (3.14) |
т.е. 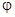 (x)= 2 - ln x. Продифференцируем функцию
(x)= 2 - ln x. Продифференцируем функцию 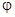 (x):
(x):  (x)= -
(x)= - 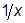 .Условие сходимости метода выполняется при ½ x ½ > 1. Это значит, учитывая область расположения корня, что вычислительный процесс метода простых итераций будет сходящимся, если исходное уравнение преобразовано к виду (3.14).
.Условие сходимости метода выполняется при ½ x ½ > 1. Это значит, учитывая область расположения корня, что вычислительный процесс метода простых итераций будет сходящимся, если исходное уравнение преобразовано к виду (3.14).
Существует более или менее универсальный способ преобразования уравнения (3.1) к виду (3.8):
| F (x) = 0 | Þ | C . F (x) = 0 | Þ | C . F (x) + x = x | (3.15) |
Здесь C - некоторый параметр, выбираемый из условия сходимости процесса.
Для примера попытаемся применить этот способ для решения уравнения (3.11). Условие сходимости (3.9) для преобразования (3.15) в общем виде выглядит так:
 .
.
так как в этом неравенстве присутствует знак модуля, то оно распадается на два неравенства:
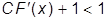 и
и 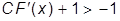
или
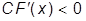 и и 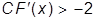 . .
| (3.16) |
Дальнейшее преобразование этих неравенств для получения условия на значения параметра С зависит от знака производной  в окрестности искомого корня.
в окрестности искомого корня.
Так как в уравнении (3.11) 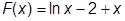 , то неравенства (3.16) для него выглядят так:
, то неравенства (3.16) для него выглядят так:
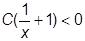 и и 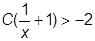 . .
| (3.17) |
В качестве окрестности корня уравнения (3.11) рассматриваем интервал [1, 2], полученный на этапе отделения корней. Вычислим значения производной  при х =1 и х =2:
при х =1 и х =2:
 и
и  .
.
Так как производная в исследуемой окрестности положительна, то неравенства (3.17) можно записать так:
С < 0 и C > 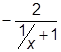
| (3.18) |
Подставим во второе из этих неравенств границы нашей окрестности и получим:
для х =1 → С >-1, для х =2 → C >-4/3.
Следовательно, из (3.18) получаем
- 1 < С < 0 или -4/3 < С <0.
Выбирая меньший по длине из этих двух промежутков, окончательно получаем:
- 1 < С < 0,
т.е. для любого значения С из интервала от –1 до 0 мы будем иметь сходящийся метод простых итераций для уравнения ln x - 2 + x = 0, преобразованного к виду x = 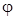 (x), где
(x), где  (x)= С (ln x - 2 + x)+х. На практике в качестве конкретного значения С берется обычно средина найденного интервала. В нашем примере это будет С =-0,5
(x)= С (ln x - 2 + x)+х. На практике в качестве конкретного значения С берется обычно средина найденного интервала. В нашем примере это будет С =-0,5
При использовании преобразования (3.15) условием окончания вычислительного процесса является выполнение неравенства

 .
.
В приводимой на рис.3.12. блок-схеме использован описанный способ (3.15) преобразования исходного уравнения к виду (3.8). В программе необходимо указывать функцию F (x) и вводить вычисленный заранее параметр С и значение допустимой погрешности  .
.

Рис.3.12. Алгоритм метода простых итераций:
В соответствии с этим алгоритмом программа должна осуществлять не более 100 итераций. Если за 100 итераций не достигнута требуемая точность, то программа выводит сообщение об отсутствии сходимости и прекращает работу.