Лекция 13. Шум от квантования сигнала.
Multiresolution - переменная разрешающая способность
Пусть справедливо дополнительное предположение:  . Из включения
. Из включения 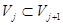 вытекает представление
вытекает представление 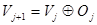 , где
, где 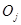 - ортогональное дополнение пространства
- ортогональное дополнение пространства 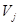 до пространства
до пространства 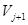 . При сделанных предположениях пространство
. При сделанных предположениях пространство 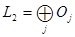 ,и любая функция
,и любая функция 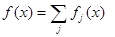 , где
, где 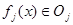 . Последнее разложение интерпретируется как представление функции с нарастающей степенью детализации, которое и получило название Multiresolution. Если в качестве материнской функции выбрана функция
. Последнее разложение интерпретируется как представление функции с нарастающей степенью детализации, которое и получило название Multiresolution. Если в качестве материнской функции выбрана функция  , базис пространства
, базис пространства 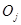 составляют функции, полученные сдвигом из
составляют функции, полученные сдвигом из 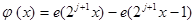
Дискретный сигнал
Начиная с этого момента дальнейшее изложение ориентируется на компьютерную обработку сигнала. Основное отличие состоит в отсутствии понятия непрерывности, на котором базировался предыдущий материал.
Шум от дискретизации
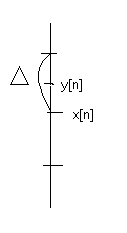
|
В результате перехода от непрерывного сигнала к дискретному возникает искажение. Реальный сигнал 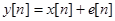 . Здесь первое слагаемое - дискретный сигнал, а второе - ошибка. Пусть
. Здесь первое слагаемое - дискретный сигнал, а второе - ошибка. Пусть 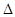 - длина интервала между соседними дискретными значениями. Предположим, что для представления сигнала используются
- длина интервала между соседними дискретными значениями. Предположим, что для представления сигнала используются 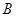 битов, а весь интервал возможных значений входного сигнала это
битов, а весь интервал возможных значений входного сигнала это 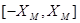 . Тогда имеет место равенство
. Тогда имеет место равенство 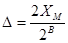 . В процессе дискретизации вместо самого сигнала берется ближайшее возможное дискретное значение. В силу этого,
. В процессе дискретизации вместо самого сигнала берется ближайшее возможное дискретное значение. В силу этого, 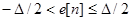 . Согласно простейшей модели,
. Согласно простейшей модели, 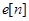 имеет равномерное распределение на интервале изменения, поэтому дисперсия
имеет равномерное распределение на интервале изменения, поэтому дисперсия  . Качество процедуры дискретизации определяется величиной
. Качество процедуры дискретизации определяется величиной 
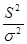 , где в числителе стоит дисперсия исходного сигнала. Заменяя
, где в числителе стоит дисперсия исходного сигнала. Заменяя 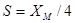 , получим
, получим 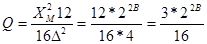 . На практике используется величина
. На практике используется величина 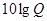 и получается результат в децибелах. В нашем случае это
и получается результат в децибелах. В нашем случае это 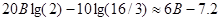 . Хороший уровень качества равен 90дБ, который достигается при B=16.
. Хороший уровень качества равен 90дБ, который достигается при B=16.
Дискретное преобразование Фурье
При машинной обработке вместо интеграла Фурье приходится пользоваться его приближением, подсчитанным с помощью конечной суммы. В результате возникают дополнительные эффекты, а теория дискретного преобразования Фурье становится самостоятельной дисциплиной.
Рассмотрим 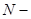 мерное пространство последовательностей длины
мерное пространство последовательностей длины  . Каждый элемент этого пространства имеет вид
. Каждый элемент этого пространства имеет вид 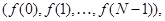 где
где 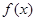 - некоторая функция, принимающая комплексные значения. В этом пространстве рассмотрим набор векторов, составленный из последовательностей
- некоторая функция, принимающая комплексные значения. В этом пространстве рассмотрим набор векторов, составленный из последовательностей 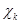 , построенных по функциям
, построенных по функциям 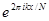 ,
, 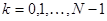 . В пространстве определено скалярное произведение:
. В пространстве определено скалярное произведение:
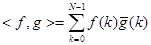 . Имеет место равенство
. Имеет место равенство 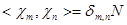 . Это означает, что последовательности
. Это означает, что последовательности 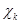 составляют базис пространства. При этом для произвольной функции
составляют базис пространства. При этом для произвольной функции 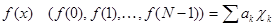 , где
, где 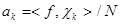 . Эти две формулы обычно записывают в виде
. Эти две формулы обычно записывают в виде
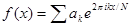 ,
, 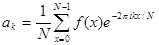 (1)
(1)
и называют дискретным преобразованием Фурье. Из последней формулы следует, что 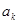 есть аналог значения преобразования Фурье исходной функции, вычисленного в точке
есть аналог значения преобразования Фурье исходной функции, вычисленного в точке 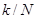 .
.
Связь ряда Фурье и дискретного преобразования Фурье
Пусть периодическая на 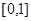 функция задана формулой
функция задана формулой
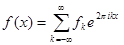 . Выберем
. Выберем  и найдем дискретное преобразование, используя значения функции в точках
и найдем дискретное преобразование, используя значения функции в точках 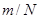 . Легко видеть, что
. Легко видеть, что 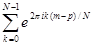 равно
равно 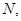 если
если 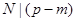 и 0 в противном случае. Отсюда следует, что коэффициент
и 0 в противном случае. Отсюда следует, что коэффициент 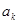 в формуле (1), найденный по последовательности
в формуле (1), найденный по последовательности 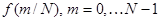 , равен
, равен 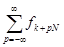 . Этот эффект называют эффектом подмены частот, поскольку вместе с ожидаемой частотой в этот коэффициент вносят вклад и другие частоты
. Этот эффект называют эффектом подмены частот, поскольку вместе с ожидаемой частотой в этот коэффициент вносят вклад и другие частоты