ЛЕКЦИЯ
МАРКОВСКИЕ ЦЕПИ
 |
 |
 |
Зависимость суммарного дохода от числа шагов
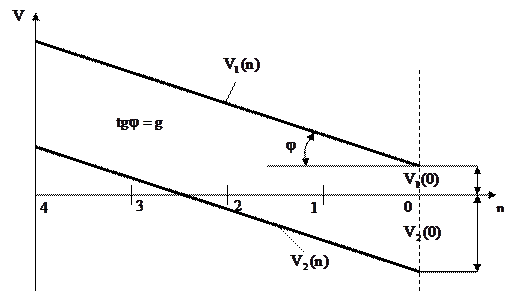
Управляемая МЦ с двумя состояниями S1 и S2.
прямая V1(n) показывает зависимость суммарного дохода, если система “стартовала” из состояния S1. Соответственно, прямая V2(n) изображает ту же зависимость для состояния S2.
Обе прямые описываются линейными уравнением: Vi(n)=ng+Vi(0),
где
g - угловой коэффициент прямой Vi(n);
Vi(0) - доход в i -том состоянии в конце процесса.
№1
Перед испытуемым находятся два табло с синими и зелеными лампочками. Последовательности зажигания описываются Марковскими цепями с матрицами перехода за один шаг
1) 
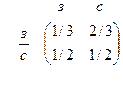2) 
.
Испытуемый должен нажать на кнопку, если на обоих табло зажегся зеленый свет.
Определить с какой вероятностью после двух правильных нажатий подряд он может ожидать ситуацию, когда не надо нажимать?
Ответ: 2/9.
№2
Известно, что если погоду в данной местности характеризовать только следующими состояниями: облачно, дождь и хорошая погода, то запись текущей погоды образует марковскую цепь с матрицей вероятностей перехода 
. Предскажите погоду на один и на два дня вперед, если сегодня погода хорошая. Имеет ли смысл пользоваться монетой, для того, чтобы решить, брать ли с собой зонтик, выходя из дому? Предполагается, что погода устойчива в течение дня.
Ответ: (0,42;0,52;0,06). Нет.
Для иллюстрации приведем конкретный числовой пример: пусть известны значения переходных вероятностей матрицы 
с одним поглощающим состоянием: 
; 
; 
; 
; 
; 
; 
; 
.
Переходная матрица в блочной системе будет выглядеть так:
В данном случае
; 
; 
; 
Проделаем необходимые вычисления:
;
;
.
В данном случае компоненты вектора 
означают, что если процесс начинается с состояния 
, то общее среднее число шагов процесса до поглощения будет равно 3,34 и, соответственно, если процесс начинается с состояния 
, то - 2,26.
В конкретных задачах, конечно, более информативным результатом будет не количество шагов, а какие-либо временные или экономические показатели. Этот результат легко получить, если связать пребывание в каждом состоянии с соответствующими характеристиками. Очевидно, набор этих характеристик составит вектор, на который нужно умножить 
слева.
Так, если задать в нашем примере время пребывания в состоянии 
, а в состоянии - 
, то общее время до поглощения будет равно:
В случаях, когда марковская цепь включает несколько поглощающих состояний, возникают такие вопросы: в какое из поглощающих состояний цепь попадет раньше (или позже); в каких из них процесс будет останавливаться чаще, а в каких - реже? Оказывается, ответ на эти вопросы легко получить, если снова воспользоваться фундаментальной матрицей.
Обозначим через 
вероятность того, что процесс завершится в некотором поглощающем состоянии 
при условии, что начальным было состояние 
. Множество состояний снова образует матрицу, строки которой соответствуют невозвратным состояниям, а столбцы - всем поглощающим состояниям. В теории ДМЦ доказывается, что матрица В определяется следующим образом:
(8.9)
Где
М - фундаментальная матрица с размерностью S;
R - блок фундаментальной матрицы с размерностью r.
 |
Рассмотрим конкретный пример системы с четырьмя состояниями
, два из которых- 
- поглощающие, а два - 
- невозвратные (рис.10):
Рис. 8.10. Система с четырьмя состояниями
Для наглядности и простоты вычислений обозначим переходные вероятности следующим образом:
; 
; 
Остальные значения вероятностей будут нулевыми. Каноническая форма матрицы перехода в этом случае будет выглядеть так:
Фундаментальная матрица после вычислений примет вид:
Тогда, согласно формуле (9), матрица вероятностей поглощения вычисляется так:
.
Поясним вероятностный смысл полученной матрицы с помощью конкретных чисел. Пусть 
, а 
. Тогда после подстановки полученных значений в матрицу 
получим:
Таким образом, если процесс начался в 
, то вероятность попадания его в 
равна 
, а в - 
. Отметим одно интересное обстоятельство: несмотря на то, что, казалось бы, левое поглощающее состояние (“левая яма”) находится рядом с , но вероятность попадания в нее почти в два раза меньше, чем в “удаленную яму” - . Этот интересный факт подмечен в теории ДМЦ, и объясняется он тем, что 
, то есть процесс имеет как бы “правый уклон”. Рассмотренная выше модель называется в теории ДМЦ моделью случайного блуждания. Такими моделями часто объясняются многие физические и технические явления и даже поведение игроков во время различных игр.
В частности, в рассмотренном примере объясняется тот факт, что более сильный игрок может дать заранее значительное преимущество (“фору”) слабому противнику и все равно его шансы на выигрыш будут более предпочтительными.
Кроме указанных выше средних характеристик вероятностного процесса с помощью фундаментальной матрицы можно вычислить моменты и более высоких порядков. В частности, дисперсия числа пребывания в том или ином состоянии - D определяется с помощью следующей матрицы:
(10)
Где
- диагональная матрица, т.е. матрица, полученная из М путем оставления в ней лишь диагональных элементов и замены остальных элементов нулями. Например, приведенная выше матрица (7а) будет иметь вид:
В свою очередь, матрица М представляет собой матрицу, полученную из М путем возведения в квадрат каждого ее элемента, то есть для (7а) будем иметь:
Аналогичным образом определяема и дисперсия для общего количества раз пребывания в том или ином состоянии 
. Обозначим ее 
:
(11)
Эргодические цепи
Оказывается, из этого условия вытекают некоторые замечательные свойства регулярных ДМЦ:
1. Степени 
при 
стремятся к стохастической матрице 
.
2. Каждая строка матрицы 
представляет один и тот же вероятностный вектор
(12)