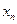
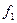
| 
| 
| 
| 
| 
| 
|
|
| ||||||
|
| ||||||
|
|
|
|
|
| |
|
| ||||||
|
|
– множество номеров наборов аргументов, на которых 
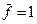или 
.
Теорема 6.
Любая ФАЛ кроме константы 1 может быть представлена в виде
Алгоритм получения совершенной нормальной формы для стрелки Пирса:
1. Выбираем те наборы, на которых f = 0.
2. Выписываем наборы со стрелками Пирса, причём 
3. Объединяем все наборы стрелками Пирса.
Пример.
|
|
| 
| 
| |
| ü | ||||
| ü | ||||
| ü | ||||
| ü | ||||
Замечание.
Если функция принимает значение 0 только на одном наборе, то берём отрицание.
Лекция № 3.
КЛАССЫБУЛЕВЫХ ФУНКЦИЙ.
1. Класс булевых функций, сохраняющих константу 0.
Их число – половина от общего числа БФ, т. е.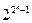 
.
2. Класс булевых функций, сохраняющих константу 1.
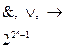
3. Класс самодвойственных функций.
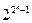
4. Линейные функции.
5. Монотонные функции.
Определение 1.
Функция 
называется двойственной с функцией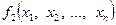 
, если 
.
Определение 2.
Функция называется самодвойственной, если она двойственна к самой себе.
Определение 3.
Функция 
называется линейной, если 
, где 
. Конъюнкция и дизъюнкция не линейные функции.
Определение 4.
Рассмотрим два набора значений аргументов 
. Функция называется монотонной, если для любых наборов 
, т. е. 
, 
.
Полная система функций.
Определение 5.
Система булевых функций 
называется полной в некотором классе R, если любая функция может быть представлена суперпозицией 
.
Пример.
Полную систему назовём базисом. Удаление любой функции из базиса приведёт к разрушению системы.
Минимальные базисы:
1. 
2. 
3. 
4. 
Определение 6.
Множество M – замкнутый класс, если любая суперпозиция функций снова принадлежит M.
Множество линейных функций – замкнутый класс.
Теорема 1.
Всякая булева функция, не содержащая отрицаний, представляет собой монотонную функцию (не константа). И наоборот: для любой монотонной функции (не константы) существует булева функция без отрицаний.
4 
Пусть имеем БФ без отрицаний. Приведём её к ДНФ.
Возьмём набор аргументов 
.
Пусть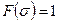 
, тогда
Теперь рассмотрим набор 
.
Условие монотонности выполняется.
f – монотонная БФ, отличная от 0 и 1. Она имеет ДНФ. Все содержащиеся в ДНФ конъюнкции будем называть импликантами. Пусть в этой функции существует импликант вида 
, где K – все остальные элементы конъюнкции. Тогда на любом наборе, в котором 
, 
.
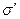получается из 
.
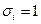Таким образом, 
также будет импликантой.
не может быть простой импликантой, т. е. все конъюнкции без отрицания. 3
Теорема 2.
Множество любых монотонных функций есть замкнутый класс.
4 Следует из предыдущей теоремы, т. к. подстановка формулы без отрицаний в формулу без отрицаний даст формулу без отрицаний. 3
Следствие 1.
Класс монотонных функций – замыкание системы 
. Любая БФ – суперпозиция 
.
Теоремы о полноте.
Лемма 1.
О немонотонных функциях.
Если не монотонна, то подстановкой констант можно получить отрицание. Точнее из n-1 констант.
4 Пусть f не монотонна: 
. Если 
и 
отличаются k компонентами, то в в k стоят 0, а в в k стоят 1.
Будем заменять в 0 на 1 по одной.
Возьмём 
.
Пусть 
и 
отличаются в i-ой компоненте. Тогда 
.
Подставим в f и .
3
Лемма 2.
О нелинейных функциях.
Если БФ нелинейна, то с помощью подстановки констант и использования отрицаний можно получить 
и 
, т. е. существует представление и в виде суперпозиции констант, отрицаний и самой функции f.
4 Пусть f нелинейна, тогда её полином Жегалкина содержит конъюнкцию переменных 
.
Пусть 
, а все 
.
Тогда, подставив константы в полином Жегалкина, останутся 
. Т. о. функция имеет вид 
, где 
– константы 0 или 1. Т. о. получаем таблицу:
| 
| 
| 
| Вид полинома | Эквивалентная БФ | Искомая суперпозиция |
| 
|
| 
| |||
| 
| 
| 
| |||
| 
| 
| 
| |||
| 
| 
| 
| |||
| 
| 
| 
| |||
| 
| 
| 
| |||
| 
| 
| 
| |||
| 
| 
| 
|
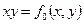
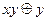
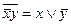
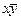
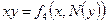
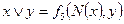
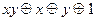
В последнем столбце искомое представление в виде конъюнкции или дизъюнкции. 3
Пример.
Важны места в функции, а именно 1-ое и 3-е.
Схема реализации функции: номера мест – номера входов в схему. Две леммы позволяют получить все булевы операции с помощью нелинейных, немонотонных, и констант 0 и 1. Это ещё не полнота в сильном смысле.
Лекция № 4.
ТЕОРЕМЫО ПОЛНОТЕ (продолжение).
Определение 1.
Система функций 
называется функционально полной в слабом смысле, если любая БФ может быть представлена 
, т. е. может быть представлена суперпозицией констант 0, 1 и функций из .
Теорема 1.
О функциональной полноте в слабом смысле.
Для того чтобы система функций была функционально полной в слабом смысле необходимо и достаточно, чтобы она содержала хотя бы одну немонотонную и хотя бы одну нелинейную функцию.
4 Если не содержит немонотонных и нелинейных функций, то их нельзя получить с помощью суперпозиции из 
.
Пусть содержит немонотонную и нелинейную функцию. Тогда по лемме 1 получаем отрицание, а из леммы 2 получаем необходимые дизъюнкции и конъюнкции. 3
Пример.
| 
| 
| 
| |
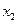
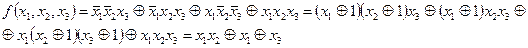
Нелинейная и немонотонная функция.
Утверждение 1.
Класс самодвойственных функций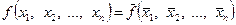 
является замкнутым.
4 Пусть 
и 
самодвойственны.
Подставим в вместо 
:
, т. е. g тоже замкнута. 3
Теорема 2.
Поста (в сильном смысле).
Для того чтобы система была функционально полной в сильном смысле необходимо и достаточно, чтобы она содержала:
1. Функцию, не сохраняющую ноль.
2. Функцию, не сохраняющую единицу.
3. Нелинейную функцию.
4. Немонотонную функцию.
5. Самодвойственную функцию.
4 
Следует из замкнутости всех пяти классов.
Если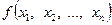 
не самодвойственна, то подстановкой 
и 
можно получить константу:
Тогда функция 
.
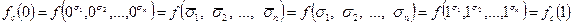
а) Пусть теперь 
не сохраняет 0, а 
не сохраняет 1. не самодвойственна.
есть 1. 
по определению.
б) Если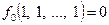 
, то 
, так как по определению и 
.
Тогда из подстановкой и 
получаем 
, являющуюся константой.
Используя ещё раз получаем другую константу.
Таким образом 
.
Этого достаточно для получения константы 0 и 1.
Таким образом, используя получение 0 и 1 и теорему о слабой полноте, получили теорему о сильной полноте. 3
Лекция № 5.
ГЕОМЕТРИЧЕСКАЯ ИНТЕРПРЕТАЦИЯ БУЛЕВЫХ ФУНКЦИЙ.
Определение 1.
Конъюнкция называется элементарной, если любая переменная встречается не более одного раза.
Определение 2.
ДНФ называется минимальной, если она содержит наименьшее количество букв по сравнению со всеми другими ДНФ, эквивалентными исходной. Обозначим её МДНФ.
Будем считать набор аргументов 
точками n -мерного пространства. Тогда функцией будет n -мерный куб.
Определение 3.
Интервалом k-ого ранга будем называть подмножество вершин n -мерного куба, соответствующей конъюнкции k -ого ранга.
Интервал большего ранга покрывает интервал меньшего ранга.
Пример.
Определение 4.
Интервал I называется максимальным, если не существует 
и 
, где 
– множество наборов значений аргументов, на которых функция равна 1.
Определение 5.
ДНФ, полученная покрытием множества максимальными интервалами, называется сокращенной ДНФ (СокДНФ).