повышенный уровень, время – 2 мин)

Тема: Составление запросов для поисковых систем с использованием логических выражений.

Что нужно знать:

· таблицы истинности логических операций «И», «ИЛИ», «НЕ» (см. презентацию «Логика»)

· если в выражении нет скобок, сначала выполняются все операции «НЕ», затем – «И», затем – «ИЛИ»

· в поисковых запросах операция «НЕ» обозначается знаком ~, операция «И» обозначается знаком &, а операция «ИЛИ» – знаком |

· пусть A – множество страниц, на которых встречается слово A, а B – множество страниц, на которых встречается слово B; тогда

а) запрос A & B соответствует пересечению множеств A Ç B

б) запрос A|B соответствует объединению множеств A È B

· будем обозначать через N_X количество страниц, которые выдаёт поисковая система по запросу X

· для двух областей справедлива формула включений и исключений, которая позволяет легко решать все задачи с двумя областями:

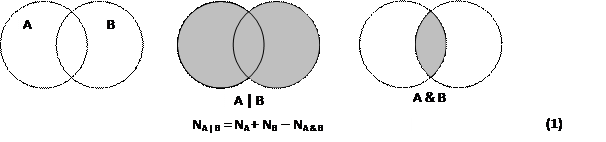
· эту формулу можно переписать в разных формах в зависимости от того, что требуется найти, например,

N_{A & B} = N_A + N_B – N_{A | B} N_A = N_{A & B} + N_{A | B} – N_B N_A + N_B = N_{A & B} + N_{A | B}

· равенство сохраняется, если каждая из 4-х областей заменяется на её пересечение с третьей областью C:

таким образом, если все 4 запроса имеют вид X & C, область C при вычислениях можно игнорировать (это равносильно переходу от областей A и B к областям A’ = A & C и B’ = B & C, что не изменяет результата)

· формула включений и исключений для трёх областей выглядит так:

N_{A | B | C} = N_A + N_B + N_C – N_{A & B} – N_{A & C} – N_{B & C} + N_{A & B & C} (2)

Пример задания:

Р-09 [1]. В таблице приведены запросы и количество найденных по ним страниц некоторого сегмента сети Интернет. Знак & обозначает логическую операцию «И», знак «|» – операцию «ИЛИ», и знак «~» – операцию «НЕ».

Запрос	Количество страниц (тыс.)
Лето
Пляж
Море
Лето & Пляж
Лето & Пляж & Море

Определите максимальное количество страниц (в тысячах), которое может быть найдено по запросу

Лето | Пляж | Море

Считается, что все запросы выполнялись практически одновременно, так что набор страниц, содержащих все искомые слова, не изменялся за время выполнения запросов.

Решение:

1) особенность этой задачи: требуется найти МАКСИМАЛЬНОЕ количество страниц, которое может быть найдено по некоторому запросу, то есть определить это количество однозначно не получится

2) построим диаграмму Эйлера-Венна и обозначим числами получившиеся области:

3) запишем равенства, которые следуют из условия:

Лето	1 + 2 + 4 + 5 = 79
Пляж	4 + 5 + 6 + 7 = 85
Море	2 + 3 + 5 + 6 = 40
Лето & Пляж	4 + 5 = 20
Лето & Пляж & Море	5 = 7

Здесь и далее для сокращения записи допускается некоторая неточность в обозначениях: равенство 1 + 2 + 4 + 5 = 79 строго должно быть записано как N ₁ + N ₂ + N ₄ + N ₅ = 79, где N _i – количество результатов в области с номером i.

4) учитывая последние два равенства в таблице, исключаем области 4 и 5 и получаем систему уравнений, связывающую размеры оставшихся областей:

1 + 2 = 59, 6 + 7 = 65, 2 + 3 + 6 = 33

5) нас интересует область Лето | Пляж | Море, то есть

1 + 2 + 3 + 4 + 5 + 6 + 7 =?

6) подставляя известные размеры областей (1+2), (4+5) и (6+7), получаем

59 + N ₃ + 20 + 65 = 144 + N ₃

7) остаётся определить возможные размеры области 3; они ограничены равенством

2 + 3 + 6 = 33

то есть, N ₃ £ 33 при N ₂ = N ₆ = 0.

8) однако возможно, что минимальные размеры областей 2 и 6 ограничены, это нужно проверить. Оставшиеся условия

1 + 2 = 59, 6 + 7 = 65

говорят о том, что таких ограничений нет, и области 2 и 6 могут иметь нулевой размер.

9) поэтому максимальное количество результатов по заданному запросу равно 144 + 33 = 177.

10) Ответ: 177.

Решение, формула включений и исключений (А.Н. Носкин):

1) По формуле включений-исключений получаем:

Лето | Пляж = Лето + Пляж - Лето & Пляж = 79 + 85 – 20 = 144

2) Тогда, для получения максимального результата Лето | Пляж | Море, необходимо определить значение только одной области – «3» и чтобы она имела максимальный размер. Ее размер можно найти из запроса «Море»: «2 + 3 + 5 + 6» = 40, при этом учитываем, что область «5» = 7 и предполагая, что область «2» и «6» равны 0, то есть область «3» может иметь максимальный размер = 33

3) поэтому максимальное количество результатов по заданному запросу равно 144 + 33 = 177.

4) Ответ: 177.

Ещё пример задания:

Р-08. В таблице приведены запросы и количество найденных по ним страниц некоторого сегмента сети Интернет. Знак & обозначает логическую операцию «И», знак «|» – операцию «ИЛИ», и знак «~» – операцию «НЕ».

Запрос	Количество страниц (тыс.)
Робот & (Ум | Интеллект)
Ум & Робот
Ум
Интеллект & Робот
Интеллект
~Робот & Ум & Интеллект

Сколько страниц (в тысячах) будет найдено по запросу

Ум | Интеллект

Считается, что все запросы выполнялись практически одновременно, так что набор страниц, содержащих все искомые слова, не изменялся за время выполнения запросов.

Решение:

1) особенность этой задачи: нет ни одной пары областей, которые не пересекаются!

2) нарисуем диаграмму Эйлера-Венна для трёх областей (Р – Робот, У – Ум, И – Интеллект):

3) будем обозначать через N _x число найденных элементов в области с номером X

4) запишем области, которые фигурируют в запросах, как сумму непересекающихся областей, и выпишем равенства, которые следуют из данных в таблице:

Запрос				№
Робот & (Ум | Интеллект)	2 + 4 + 5	N 2 + N 4 + N 5 =		(1)
Ум & Робот	2 + 5	N 2 + N 5 =		(2)
Ум	2+ 3 + 5 + 6	N 2 + N 3 + N 5+ N 6 =		(3)
Интеллект & Робот	4 + 5	N 4 + N 5 =		(4)
Интеллект	4 + 5 + 6 + 7	N 4 + N 5 + N 6+ N 7 =		(5)
~Робот & Ум & Интеллект		N 6 =		(6)
Ум | Интеллект	2 + 3 + 4 + 5 + 6 + 7	N 2 + N 3 + N 4 + N 5 + N 6+ N 7 =	X	(7)

5) из таблицы видно, что величину одной области (6) мы уже знаем N ₆ = 20

6) подставляя (5) в (7), получаем

X = N ₂ + N ₃ + N ₄ + N ₅ + N ₆+ N ₇ = N ₂ + N ₃ + 200

7) из (3) находим N ₂ + N ₃ = 210 – N ₅ – N ₆ = 210 – N ₅ – 20 = 190 – N ₅

8) вычитая (4) из (1), получаем N ₂ = 30, и из (2) находим N ₅ = 60 – N ₂ = 30

9) тогда X = N ₂ + N ₃ + 200 = 190 – 30 + 200 = 360.

10) Ответ: 360.

Решение (вариант 2, Р.А. Еннер):

1) Обозначим множества: Р = Робот, У = Ум, И = Интеллект

2) по распределительному закону

Робот & (Ум | Интеллект) = Р&(У|И) = Р&У | Р&И

3) Введем обозначения: A = Р&У, B = Р&И

Тогда Р&У | Р&И = A|B

4) по формуле включений и исключений (1) найдем

A&B = A + B - A|B = 60 + 70 – 100 = 30

5) используя закон повторения, получаем

A&B = (Р&У) & (Р&И) = Р&У&И

6) ~Р&У&И = У&И – Р&У&И (см. рис)

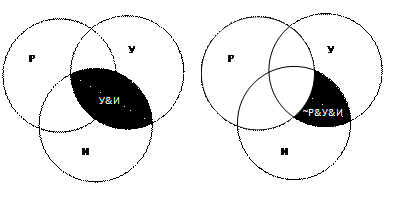
7) Отсюда: У&И = ~Р&У&И + Р&У&И = 20 + 30 = 50

8) по формуле включений и исключений: У + И = У|И + У&И находим:

У|И = У + И - У&И = 210 + 200 – 50 = 360

9) Ответ: 360.

Пример задания:

Р-07. В таблице приведены запросы и количество найденных по ним страниц некоторого сегмента сети Интернет:

Запрос	Количество страниц (тыс.)
США | Япония | Китай
Япония | Китай
(США & Япония) | (США & Китай)

Сколько страниц (в тысячах) будет найдено по запросу

США

Считается, что все запросы выполнялись практически одновременно, так что набор страниц, содержащих все искомые слова, не изменялся за время выполнения запросов.

Решение:

1) заметим, что в силу тождества последний запрос в таблице равносилен такому:

(США & Япония) | (США & Китай) Û США & (Япония | Китай)

2) тогда вводя обозначение для областей

A = США, B = Япония | Китай,

получаем стандартную задачу с двумя переменными:

Запрос	Количество страниц (тыс.)
А | B
B
А & B
А	?

3) имеем по формуле (см. решения ниже)

N_A = N_A|B - N_B + N_A&B = 450 – 260 + 50 = 240

4) Ответ: 240

Ещё пример задания:

Р-06. В таблице приведены запросы и количество найденных по ним страниц некоторого сегмента сети Интернет:

Запрос	Количество страниц (тыс.)
Ростов & (Орёл & Курск | Белгород)
Ростов & Белгород
Ростов & Орёл & Курск & Белгород

Сколько страниц (в тысячах) будет найдено по запросу

Ростов & Орёл & Курск

Считается, что все запросы выполнялись практически одновременно, так что набор страниц, содержащих все искомые слова, не изменялся за время выполнения запросов.

Решение:

1) заметим, что во всех четырёх запросах есть «сомножитель» «Ростов &», поэтому эта задача равносильна такой:

Запрос	Количество страниц (тыс.)
Орёл & Курск | Белгород
Белгород
Орёл & Курск & Белгород
Орёл & Курск	?

2) теперь обозначим A = Орёл & Курск и получим задачу с двумя областями:

Запрос	Количество страниц (тыс.)
A | Белгород
Белгород
A & Белгород
A	?

3) по формуле для задачи с двумя областями (см. задачи, разобранные ниже)

N_A|B = N_A + N_B - N_A&B

получаем

N_A = N_A|B - N_B + N_A&B

4) вычисляем: 370 – 204 + 68 = 234.

5) Ответ: 234.

Решение (вариант 2, Р.А. Еннер):

1) Обозначим множества: Р = Ростов, О = Орёл, К = Курск, Б = Белгород

2) по распределительному закону

Ростов & (Орёл & Курск | Белгород) = Р&(О&К | Б) = Р&О&К | Р&Б

3) Введем обозначения: A = Р&О&К, B = Р&Б, тогда A | B = Р&О&К | Р&Б

4) по закону повторения A&B = Р&О&К & Р&Б = Р&О&К&Б

5) по формуле включений и исключений (1) найдем A = A|B + A&B – B = 370 + 68 – 204 = 234

6) Р&О&К = A = 234

7) Ответ: 234.

Ещё пример задания:

Р-05. В таблице приведены запросы и количество найденных по ним страниц некоторого сегмента сети Интернет:

Запрос	Количество страниц (тыс.)
Ухо
Подкова
Наковальня
Ухо | Подкова | Наковальня
Ухо & Наковальня
Ухо & Подкова

Сколько страниц (в тысячах) будет найдено по запросу

Подкова & Наковальня

Считается, что все запросы выполнялись практически одновременно, так что набор страниц, содержащих все искомые слова, не изменялся за время выполнения запросов.

Решение (вариант 1, рассуждения по диаграмме):

1) построим диаграмму Эйлера-Венна

2) количество сайтов, удовлетворяющих запросу в области i, будем обозначать через N_i

3) здесь 5 областей, причём известны следующие данные:

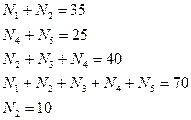
4) нас интересует область 4. Находим ответ прямой подстановкой:

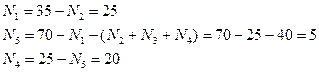
5) таким образом, ответ – 20.

Решение (вариант 2, рассуждения по диаграмме):

1) пп. 1-2 такие же, как в варианте 1

2) заметим, что в прямую сумму величин областей Ухо, Подкова и Наковальня дважды входят области 2 и 4, поэтому для вычисления 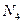достаточно вычесть из суммы Ухо+Подкова+Наковальня размер их объединения (Ухо | Подкова | Наковальня) и величину области 2 (Ухо & Наковальня).

3) тогда сразу получаем

.

4) ответ – 20.

Решение (вариант 3, Р.А. Еннер):

1) Обозначим множества: У = Ухо, П = Подкова, Н = Наковальня

2) Заметим: из того что У&П = 0 очевидно следует У&П&Н = 0

3) Подставляем все данные в формулу включений и исключений (2):

У + П + Н = У|П|Н + У&П + П&Н + У&Н – У&П&Н

35 + 25 + 40 = 70 + 0 + П&Н + 10 - 0

4) решая уравнение, получим П&Н = 20

5) Ответ: 20.

Еще пример задания:

Р-04. В таблице приведены запросы и количество страниц, которые нашел поисковый сервер по этим запросам в некотором сегменте Интернета:

Запрос	Количество страниц (тыс.)
пирожное & выпечка
пирожное
выпечка

Сколько страниц (в тысячах) будет найдено по запросу

пирожное | выпечка

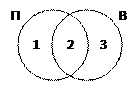Решение (вариант 1, рассуждения по диаграмме):

1) построим диаграмму Эйлера-Венна, обозначив области «пирожное» (через П) и «выпечка» (В):

2) количество сайтов, удовлетворяющих запросу в области i, будем обозначать через N_i

3) несложно сообразить, что число сайтов в интересующей нас области равно

N₁ + N₂ + N₃ = (N₁ + N₂) + (N₃ + N₂) – N₂

4) поскольку нам известно, что по условию

N₁ + N₂ = 8700

N₃ + N₂ = 7500

N₂ = 3200

сразу получаем

N₁ + N₂ + N₃ = 8700 + 7500 - 3200 = 13000

5) таким образом, ответ – 13000.

Решение (вариант 2, общая формула):

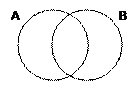
1) сначала выведем формулу, о которой идет речь; построим диаграмму Эйлера-Венна для двух переменных A и B:

2) обозначим через N_A, N_B, N_A&B и N_A|B число страниц, которые выдает поисковый сервер соответственно по запросам A, B, A & B и
A | B

3) понятно, что если области A и B не пересекаются, справедлива формула N_A|B=N_A+N_B

4) если области пересекаются, в сумму N_A+N_B область пересечения N_A&B входит дважды, поэтому в общем случае

N_A|B = N_A + N_B - N_A&B

5) в данной задаче

N_П = 8700, N_В = 7500, N_П&В = 3200

6) тогда находим число сайтов в интересующей нас области по формуле

N_П|B = N_П + N_B – N_П&B = 8700 + 7500 – 3200 = 13000

7) таким образом, ответ – 13000.

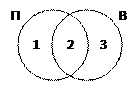Решение (вариант 3, решение системы уравнений):

1) нарисуем области «пирожное» (обозначим ее через П) и «выпечка» (В) в виде диаграммы (кругов Эйлера); при их пересечении образовались три подобласти, обозначенные числами 1, 2 и 3;

2) составляем уравнения, которые определяют запросы, заданные в условии:

пирожное & выпечка N₂ = 3200

пирожное N₁ + N₂ = 8700

выпечка N₂ + N₃ = 7500

3) подставляя значение N₂ из первого уравнения в остальные, получаем

N₁ = 8700 - N₂ = 8700 – 3200 = 5500

N₃ = 7500 - N₂ = 7500 – 3200 = 4300

4) количество сайтов по запросу пирожное | выпечка равно

N₁ + N₂ + N₃ = 5500 + 3200 + 4300 = 13000

5) таким образом, ответ – 13000.

Еще пример задания:

Р-03. В таблице приведены запросы и количество страниц, которые нашел поисковый сервер по этим запросам в некотором сегменте Интернета:

Запрос	Количество страниц (тыс.)
Динамо & Рубин
Спартак & Рубин
(Динамо | Спартак) & Рубин

Сколько страниц (в тысячах) будет найдено по запросу

Рубин & Динамо & Спартак

Решение (вариант 1, круги Эйлера, полная диаграмма):

1) в этой задаче неполные данные, так как они не позволяют определить размеры всех областей; однако их хватает для того, чтобы ответить на поставленный вопрос

2) обозначим области, которые соответствуют каждому запросу

Запрос	Области	Количество страниц (тыс.)
Динамо & Рубин	1+2
Спартак & Рубин	2+3
(Динамо | Спартак) & Рубин	1+2+3
Рубин & Динамо & Спартак		?

3) из таблицы следует, что в суммарный результат первых двух запросов область 2 входит дважды (1 + 2 + 2 + 3), поэтому, сравнивая этот результат с третьим запросом (1 + 2 + 3), сразу находим результат четвертого:

N₂ = (320 + 280) – 430 = 170

4) таким образом, ответ – 170.

Решение (вариант 2, круги Эйлера, неполная диаграмма):

1) заметим, что в этой задаче все запросы (в том числе и тот, результат которого нужно найти, имеют вид

X & Рубин

2) поэтому часть «& Рубин » в каждом из запросов можно просто отбросить, тогда останется только две области:

Запрос	Количество страниц (тыс.)
Динамо-1
Спартак-1
Динамо-1 | Спартак-1

здесь добавление «-1» в имени области обозначает «пересечение с областью Рубин »

3) требуется найти размер области «Динамо-1 & Спартак-1 »

4) для диаграммы с двумя областями можно использовать общую формулу

N_A|B = N_A + N_B - N_A&B

5) из которой следует

N_A&B = N_A + N_B - N_A|B

6) в данном случае получаем

N_A&B = (320 + 280) – 430 = 170

7) таким образом, ответ – 170.

Решение (вариант 3, Р.А. Еннер):

1) Обозначим множества: Д = Динамо, С = Спартак, Р = Рубин

2) по распределительному закону

(Динамо | Спартак) & Рубин = (Д|С)&Р = Д&Р | С&Р

3) Введем обозначения: A = Д&Р, B = С&Р, тогда A|B = Д&Р | С&Р

4) по формуле включений и исключений (1) найдем

A&B = A + B – A|B = 320 + 280 – 430 = 170

5) по закону повторения A&B = Д&Р&С&Р = Р&Д&С = 170

6) Ответ: 170.

Ещё пример задания:

Р-02. В таблице приведены запросы к поисковому серверу. Расположите номера запросов в порядке возрастания количества страниц, которые найдет поисковый сервер по каждому запросу. Для обозначения логической операции «ИЛИ» в запросе используется символ |, а для логической операции «И» – &.

1) принтеры & сканеры & продажа

2) принтеры & сканеры

3) принтеры | сканеры

4) принтеры | сканеры | продажа

Решение (вариант 1, рассуждение с использованием свойств операций «И» и «ИЛИ»):

1) меньше всего результатов выдаст запрос с наибольшими ограничениями – первый (нужны одновременно принтеры, сканеры и продажа)

2) на втором месте – второй запрос (одновременно принтеры и сканеры)

3) далее – третий запрос (принтеры или сканеры)

4) четвертый запрос дает наибольшее количество результатов (принтеры или сканеры или продажа)

5) таким образом, верный ответ – 1234.

Возможные проблемы: · нужно внимательно читать условие, так как в некоторых задачах требуется перечислить запросы в порядке убывания количества результатов, а в некоторых – в порядке возрастания · можно ошибиться в непривычных значках: «И» = &, «ИЛИ» = | (эти обозначения привычны для тех, кто программирует на языке Си) · можно перепутать значение операций «И» и «ИЛИ», а также порядок выполнения цепочки операций (сначала – «И», потом – «ИЛИ») · для сложных запросов не всегда удастся так просто расположить запросы по возрастанию (или убыванию) ограничений

Решение (вариант 2, через таблицы истинности):

1) каждое из условий можно рассматривать как сложное высказывание

2) обозначим отдельные простые высказывания буквами:

A: принтеры (на странице есть слово «принтеры»)

B: сканеры

C: продажа

3) запишем все выражения-запросы через логические операции

, , ,

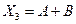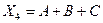
4) здесь присутствуют три переменные, А, B и C (хотя второе и третье выражения от С не зависят!), поэтому для составления таблицы истинности нужно рассмотреть 8 = 23²³³³ всевозможных комбинаций этих логических значений

5) выражение равно 1 (истинно) только при , в остальных случаях – равно 0 (ложно)

6) выражение равно 1 только при , в остальных случаях – равно 0

7) выражение 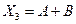равно 0 только при , в остальных случаях – равно 1

8) выражение 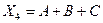равно 0 только при , в остальных случаях – 1

9) запишем результаты пп. 5-8 в виде таблицы истинности

A	B	C

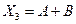
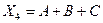
10) по таблице видим, что наименьшая «область действия» у первого выражения, поисковый сервер выдаст наименьшее число запросов

11) область, где 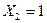, включает в себя[2] всю область, где 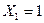и еще один вариант, поэтому «поисковик» выдаст больше запросов, чем для первого случая

12) аналогично делаем вывод, что область включает всю область 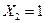и расширяет ее, а область 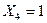– это расширение области

13) таким образом, верный ответ – 1234.

Возможные проблемы: · решение достаточно громоздко, хотя позволяет с помощью простых операций решить задачу, не рискуя ошибиться при вычислениях «в уме» в сложных случаях · если переменных более трех, таблица получается большая, хотя заполняется несложно

Решение (вариант 3, через диаграммы):

1) запишем все ответы через логические операции

, , ,

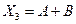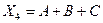
2) покажем области, определяемые этими выражениями, на диаграмме с тремя областями

3) сравнивая диаграммы, находим последовательность областей в порядке увеличения: (1,2,3,4), причем каждая следующая область в этом ряду охватывает целиком предыдущую (как и предполагается в задании, это важно!)

4) таким образом, верный ответ – 1234.

Возможные проблемы: · получается громоздкий рисунок, если используется более трех переменных (более трех кругов)

Еще пример задания:

Р-01. Некоторый сегмент сети Интернет состоит из 1000 сайтов. Поисковый сервер в автоматическом режиме составил таблицу ключевых слов для сайтов этого сегмента. Вот ее фрагмент:

Ключевое слово	Количество сайтов, для которых данное слово является ключевым
сканер
принтер
монитор
принтер | сканер
принтер & монитор
сканер & монитор

Сколько сайтов будет найдено по запросу

(принтер | сканер) & монитор

если по запросу принтер | сканер было найдено 450 сайтов, по запросу принтер & монитор – 40, а по запросу сканер & монитор – 50.

Решение (вариант 1, использованием свойств операций «И» и «ИЛИ»):

1) обратим внимание на такой факт[3] (справа указано количество сайтов по каждому запросу)

Сканер 200

Принтер 250

принтер | сканер 450

поскольку последнее число равно сумме двух предыдущих, можно сразу же придти к выводу, что в этом сегменте сети нет сайтов, на которых ключевыми словами являются одновременно принтер и сканер:

принтер & сканер 0

диаграмма Эйлера для этого случая показана на рисунке справа:

2) с этого момента все просто: для того, чтобы определить, сколько сайтов удовлетворяют заданному условию

достаточно просто сложить числа, соответствующие запросам принтер & монитор и
сканер & монитор

3) таким образом, правильный ответ: 40 + 50 = 90.

Возможные проблемы: · обратите внимание, что в условии была лишняя информация: мы нигде не использовали количество сайтов в данном сегменте Интернета (1000) и количество сайтов с ключевым словом монитор (450) · не всегда удается «раскрутить» задачу в уме, здесь это несложно благодаря «удачному» условию

Решение (вариант 3, таблицы истинности):

1) для сокращения записи обозначим через C, П, М высказывания «ключевое слово на сайте – сканер » (соответственно принтер, монитор)

2) если рассматривать задачу с точки зрения математической логики, здесь есть три переменных, с помощью которых можно составить всего 8 запросов, выдающих различные результаты

	С	П	М
?
?
?
?
?
?
?
?
всего

3) составим таблицу истинности, в которую добавим левый столбец и последнюю строку, где будем записывать количество сайтов, удовлетворяющих условиям строки и столбца (см. рисунок справа); например, первая строка соответствует сайтам, на которых нет ни одного из заданных ключевых слов; такая схема непривычна, но она существенно упрощает дело

4) сумма в последней строчке получается в результате сложения всех чисел из тех строк первого столбца, где в данном столбце стоят единицы. Например, сумма в столбце С – складывается из четырех чисел в последних четырех строчках первого столбца. Мы пока не знаем, сколько результатов возвращает каждый из восьми запросов отдельно, поэтому в первом столбце стоят знаки вопроса

5) добавим в таблицу истинности остальные запросы, которые есть в условии, в том числе и тот, который нас интересует:

П | С = принтер | сканер 450

П & М = принтер & монитор 40

C & М = сканер & монитор 50

(П | C) & М = (принтер | сканер) & монитор?

	С	П	М	П | С	П & М	C & М	(П | C) & М
?
?
?
?
?
?
всего

6) проанализируем столбец П | С в этой таблице: его сумма (450) складывается из суммы столбцов С (200) и П (250) – выделены ярким зеленым цветом – плюс последние две строчки (голубой фон), то есть, 450 = 200 + 250 + X, откуда сразу получаем, что X = 0, то есть, последним двум строчкам (запросам) не удовлетворяет ни одного сайта

7) теперь составим таблицы истинности для остальных запросов, отбросив заведомо «нулевые» варианты:

	С	П	М	П | С	П & М	C & М	(П | C) & М
?
?
?
?
всего

из оставшихся шести строк таблицы запросы П & М и С & М затрагивают только по одной строчке, поэтому сразу можем вписать соответствующие числа в первый столбец; в последнем запросе, который нас интересует, присутствуют именно эти две строки, то есть, для получения нужно сложить 40 и 50

8) таким образом, правильный ответ: 40 + 50 = 90.

Решение (вариант 3, через диаграммы и систему уравнений):

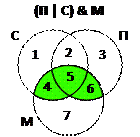
1) для сокращения записи обозначим через C, П, М высказывания «ключевое слово на сайте – сканер » (соответственно принтер, монитор) и нарисуем эти области виде диаграммы (кругов Эйлера); интересующему нас запросу (П | C) & M соответствует объединение областей 4, 5 и 6 («зеленая зона» на рисунке)

2) количество сайтов, удовлетворяющих запросу в области i, будем обозначать через N_i

3) составляем уравнения, которые определяют запросы, заданные в условии:

сканер N₁ + N₂ + N₄ + N₅ = 200

принтер N₂ + N₃ + N₅ + N₆ = 250

принтер | сканер N₁ + N₂ + N₄ + N₅ + N₃ + N₆ = 450

из первого и третьего уравнений сразу следует

200 + N₃ + N₆ = 450 Þ N₃ + N₆ = 250

далее из второго уравнения

N₂ + N₅ + 250 = 250 Þ N₂ + N₅ = 0

поскольку количество сайтов не может быть отрицательной величиной, N₂ = N₅ = 0

4) посмотрим, что еще мы знаем (учитываем, что N₅ = 0):

принтер & монитор N₅ + N₆ = 40 Þ N₆ = 40

сканер & монитор N₄ + N₅ = 50 Þ N₄ = 50

5) окончательный результат:

(принтер | сканер) & монитор N₄ + N₅ + N₆ = N₄ + N₆ = 40 + 50 = 90

6) таким образом, правильный ответ 90.

Возможные проблемы: · внимательнее с индексами переменных, очень легко по невнимательности написать N5 вместо N6 и получить совершенно другой результат · этот метод ярко демонстрирует, что в общем случае мы получаем систему уравнения с семью неизвестными (или даже с восемью, если задействована еще и область вне всех кругов); решать такую систему вручную достаточно сложно, поэтому на экзамене всегда будет какое-то условие, сильно упрощающее дело, ищите его

Еще пример задания:

Р-00. В таблице приведены запросы и количество страниц, которые нашел поисковый сервер по этим запросам в некотором сегменте Интернета:

	Запрос	Найдено страниц (тыс.)
	мезозой
	кроманьонец
	неандерталец
	мезозой | кроманьонец
	мезозой | неандерталец
	неандерталец & (мезозой | кроманьонец)

Сколько страниц (в тысячах) будет найдено по запросу

кроманьонец & (мезозой | неандерталец)

Решение (способ 1, круги Эйлера):

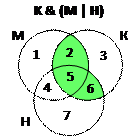
1) обозначим области «мезозой», «кроманьонец» и «неандерталец» буквами М, К и Н; пронумеруем подобласти, получившиеся в результате пересечений кругов (см. рисунок справа)

2) через N­_i обозначим количество сайтов в области с номером i

3) нас интересует результат запроса

кроманьонец & (мезозой | неандерталец)

то есть N­₂ + N₅ + N₆(зеленая область на рисунке)

4) из первых двух запросов следует, что

N₁ + N₂ + N₄ + N₅ = 50 (мезозой)

N₂ + N₃ + N₅ + N₆ = 60 (кроманьонец)

5) складывая левые и правые части уравнений, получаем

(1) N₁ + 2·N₂ + N₃ + N₄ + 2·N₅ + N₆ = 110

6) в то же время из запроса 4 получаем

(2) N₁ + N₂ + N₃ + N₄ + N₅ + N₆ = 80 (мезозой | кроманьонец)

7) вычитая из уравнения (1) уравнение (2), отдельно левые и правые части, получаем

N₂ + N₅ = 30 (мезозой & кроманьонец)

вспомним, что наша цель – определить N­₂ + N₅ + N₆, поэтому остается найти N₆

8) из запросов 1 и 3 следует, что

N₁ + N₂ + N₄ + N₅ = 50 (мезозой)

N₄ + N₅ + N₆ + N₇ = 70 (неандерталец)

9) складывая левые и правые части уравнений, получаем

(3) N₁ + N₂ + 2·N