Показатели, используемые для характеристики динамических свойств резины

Определение свойств резин при динамическом

Нагружении

Динамическое нагружение резин реализуется в амортизирующих, звукоизолирующих, противоударных и силовых резиновых технических изделиях, приводных ремнях, конвейерных лентах, уплотнениях подвижных соединений и др.

Различают упругогистерезисные и усталостнопрочностные свойства. Для характеристики упругогистерезисных свойств, описывающих взаимосвязь между напряжением и деформацией при многократном нагружении, обычно используются следующие показатели:
— эластичность по отскоку;
— динамический модуль упругости при растяжении или сжатии;
— модуль потерь при растяжении или сжатии;
— коэффициенты жесткости, характеризующие упругость и внутреннее трение;
— модуль внутреннего трения;
— коэффициент демпфирования;
— теплообразование-повышение температуры образца после многократной деформации;
— остаточная деформация после многократного сжатия.

Усталостнопрочностные свойства чаще всего характеризуют показателем усталостной выносливости, показывающим число циклов нагружения образца до разрушения. Работоспособность резин в большинстве изделии при различных условиях эксплуатации характеризуют комплексом упругогистерезисных и усталостнопрочностных показателей, взаимосвязанных между собой.

Определение упруго-гистерезисных свойств. При замкнутом процессе нагружение – разгружение (испытуемый образец возвращается к исходному состоянию нагружения) наблюдается несовпадение кривых нагружения и разгружения и образование петли гистерезиса. Площадь петли гистерезиса является мерой рассеянной механической энергии. В приборах для определения упруго-гистерезисных свойств чаще всего реализуется ударная деформация растяжения, а сами свойства оцениваются динамическим модулем, модулем внутреннего трения и эластичностью по отскоку.

Для быстрой оценки внутреннего трения и гистерезисных свойств используется их способность упруго возвращать энергию удара. На практике применяют маятниковые упругометры (эластометры), в которых замеряется угол отскока бойка от резиновой шайбы (маятник Шоба). Эластичность по отскоку - это отношение энергии, возвращенной резиновым образцом бойку после удара - W₂, к общей энергии, затраченной на удар -W_1, которое пропорционально отношению высот (углов) расположения центра тяжести бойка до и после удара:

Э = W₂/W₁ = [(1-cos a₂) / (1- cos a₁)]· 100 %,

где a₁ – угол падения маятника 90 или 60º;a₂– угол отскока маятника.

Для реальных резин этот показатель равен 40-60%.

Определение усталостно-прочностных свойств. Вследствие высокоэластических свойств резина обладает исключительно высокой способностью накапливать энергию при деформировании. При циклическом (динамическом) нагружении энергия, поглощенная при изменении конформаций молекул, разрушении связей между каучуком и наполнителем, между частицами наполнителя и др., выделяется в виде теплоты, что приводит к повышению температуры образца и снижению прочности материала. Это явление называется динамической усталостью или утомлением. Динамическая выносливость чаще всего оценивается числом циклов нагружения, которое образец выдерживает без разрушения в условиях динамических деформаций растяжения, сжатия, сдвига, изгиба, кручения или при их комплексном воздействии.

Испытания проводятся в разных режимах, которые характеризуются несколькими параметрами: амплитудой деформации, амплитудой напряжения, средними статическими значениями амплитуд, частотой нагружения при синусоидальном характере изменения переменных.

Наиболее распространен режим испытания, в котором задаются постоянными деформации – динамическая и статическая. Режим наиболее прост в конструктивном исполнении: эксцентриковые механизмы позволяют достичь постоянства амплитуды деформации, а предварительное растяжение образцов достигается линейным перемещением зажимов. Так работают машины для испытаний на многократное растяжение.

При испытаниях на многократное сжатие главной трудностью является исключение скольжения образца по рабочим площадкам прибора, что требует усложнения формы образца. При испытаниях на многократный сдвиг также возникают трудности с креплением образцов и созданием деформации, которая не должна быть больше половины высоты образца. В этих испытаниях чаще всего определяют температуру разогрева образца с помощью специальной игольчатой термопары.

В машинах для испытаний на многократный изгиб образцы закрепляются радиально в пазах диска, и при вращении диска каждый образец изгибается дважды за один оборот диска роликами, установленными по обе стороны диска. В машинах для испытаний на многократное кручение один зажим совершает возвратно-вращательное движение. Есть машины, в которых реализуется изгиб с кручением при перемещении одного зажима по дуге.

Во всех видах динамических испытаний процесс продолжается до появления первых трещин или выкрашивания мелких кусочков. Поэтому результатом испытания может быть также скорость разрастания трещин до определенной длины или площади. Момент появления трещины определяют визуально с помощью лупы, осматривая образцы через определенное время или число циклов нагружения. Из-за разброса показателей параллельно испытывают 12-18 образцов.

В отдельную группу выделяются динамические испытания в условиях концентрации напряжений на специально нанесенных повреждениях образцов - проколы, порезы, выемки и зигзагообразные канавки. Они называются испытаниями на сопротивление образованию и разрастанию трещин. Образцы подвергают изгибу и фиксируют скорость разрастания трещин до определенной длины или площади.

При динамических испытаниях за момент разрушения образца чаще всего принимают момент образования первой трещины, реже – момент разделения образца на части.

Во-первых, очень важными показателями являются жесткость и гистерезисные потери, которые можно охарактеризовать значениями G, Е и tg 5. Резины с высоким значением tg 5 используют в изделиях, предназначенных для гашения энергии колебаний (опоры двигателей, виброизоляция и др.), а резины с низким значением tg 5 применяют в машинах, работающих в резонансном режиме, предназначенных для транспортирования материалов (центрифуги, грохота, вибротранспортеры и др.). Считается, что значения tg 5 для резин с низкой и высокой степенью демпфирования должны приближаться к 0,1 и 1,0 соответственно. Эластичность по отскоку характеризует динамические свойства резин в условиях, при которых образец подвержен половинному циклу деформации. Значение S обратно пропорционально значениям G", Е", tg 5. Динамический модуль упругости возрастает при повышении твердости и снижении значения ер.

Во-вторых, при многократной деформации происходит повышение температуры (теплообразование), обусловленное гистерезисными потерями. Скорость повышения и установившаяся температура, а также ее распределение по образцу (изделию) зависят от гистерезисных потерь, теплофизических свойств резины, размера и формы образца (изделия). В режиме постоянной деформации увеличение динамической жесткости резин приводит к повышению теплообразования. Разогрев образца (изделия) важен не сам по себе, а вследствие его влияния на другие Свойства резин.

В-третьих, работоспособность изделия может понижаться в результате изменения его размеров или формы из-за процессов ползучести, релаксации напряжения или накопления остаточной деформации в процессе эксплуатации. Обычно скорости этих процессов при многократной деформации значительно выше, чем при статическом нагружении.

В-четвертых, возможно разрушение образца (изделия) вследствие усталостных процессов, ускоряемых теплообразованием.

Таким образом, влияние динамических условий нагружения на работоспособность резин неоднозначно. Например, высокие гистерезисные потери, которые необходимы для эффективного гашения колебаний, могут ускорять усталостное разрушение материала или приводить к нежелательному изменению его размеров или формы. При этом резины, механические свойства которых при статическом нагружении одинаковы, могут существенно различаться по результатам динамических испытаний.

Показатели, используемые для характеристики динамических свойств резины

Наименование показателя	Обозначение	Определение показателя
1. Динамический модуль упругости резины при растяжении или сжатии, Па (кгс/см)		Отношение составляющей нормального напряжения, совпадающей по фазе с деформацией, к деформации растяжения или сжатия (черт.2)
		1 - составляющая напряжения, совпадающая по фазе с деформацией; 2 - составляющая напряжения, сдвинутая по фазе относительно деформации на 90°; 3 - результирующее напряжение; - угол сдвига фаз между деформацией и напряжением Черт.2
2. Динамический модуль упругости резины при сдвиге, Па (кгс/см)		Отношение составляющей напряжения сдвига, совпадающей по фазе с деформацией, к деформации сдвига
3. Константа упругости (коэффициент жесткости) резины, Н/м (кгс/см)		Отношение составляющей приложенной силы, совпадающей по фазе с деформацией, к смещению
4. Средний модуль резины, Па (кгс/см)		Отношение среднего напряжения к средней деформации
5. Модуль потерь резины при растяжении или сжатии, Па (кгс/см)		Отношение составляющей нормального напряжения, сдвинутой по фазе относительно деформации на 90°, к деформации растяжения или сжатия (черт.2)
6. Модуль потерь резины при сдвиге, Па (кгс/см)		Отношение составляющей напряжения сдвига, сдвинутой по фазе относительно деформации на 90°, к деформации сдвига
7. Комплексный модуль резины при растяжении или сжатии, Па (кгс/см)		Отношение результирующего нормального напряжения к деформации растяжения или сжатия, которое представляет собой вектор, соответствующий комплексному числу
8. Абсолютная величина комплексного модуля резины при растяжении или сжатии, Па (кгс/см)
9. Комплексный модуль резины при сдвиге, Па (кгс/см)		Отношение результирующего напряжения сдвига к деформации сдвига, которое представляет собой вектор, соответствующий комплексному числу
10. Абсолютная величина комплексного модуля при сдвиге, Па (кгс/см)
11. Константа затухания резины, Н·с/м (кгс·с/м)		Отношение составляющей приложенной силы, сдвинутой по фазе относительно деформации на 90°, к скорости деформации
12. Тангенс угла механических потерь (фактор потерь) резины		Отношение модуля потерь к динамическому модулю упругости. При деформации растяжения или сжатия При деформации сдвига Векторное представление составляющих комплексного модуля () дано на черт.3
		Черт.3
13. Угол механических потерь, радиан (градус)		Угол сдвига фаз между напряжением и деформацией (см. черт.2 и 3)
14. Механический гистерезис резины	-	Несовпадение зависимостей напряжение-деформация за цикл при динамическом режиме нагружения и разгружения, имеющее следствием необратимое рассеяние энергии
15. Петля механического гистерезиса резины	-	Замкнутая кривая на диаграмме напряжение-деформация за цикл (см. черт.1)
16. Удельные механические потери резины за цикл, Дж/м(кгс·см/см)		Механическая энергия, рассеиваемая в единице объема резины за цикл деформации Это площадь петли механического гистерезиса, рассчитанная с учетом масштаба по координатам (см. черт.1)
17. Коэффициент механических потерь (относительный гистерезис) резины		Отношение механических потерь резины за цикл к полной энергии деформации цикла
18. Модуль внутреннего трения резины, Па (кгс/см)		Удвоенное значение механических потерь цикла при единичном значении амплитуды деформации
19. Эластичность по отскоку		Отношение возвращенной энергии к энергии, затраченной на деформацию образца резины при ударе
20. Логарифмический декремент затухания колебаний		Натуральный логарифм отношения двух последовательных амплитуд затухающих колебаний

1. Влияние длительности испытания на динамические свойства резин.

Динамические свойства резин могут быстро изменяться в первых циклах испытаний вследствие неустановившегося вязкоупругого поведения резины и тиксотропии структуры наполнителя. Этот эффект особенно резко проявляется в резинах, содержащих наполнители. Поэтому в начале испытаний несколько первых гистерезисных петель открыты и они асимптотически приближаются к устойчивой форме петли (петля , черт.1, приложение 1). Это изменение формы и положения петли механического гистерезиса иногда называют "дрейфом петли".

- амплитуда деформации; - средняя деформация; - петля механического гистерезиса; - минимальная деформация

При многократных деформациях механические потери могут привести к значительному разогреву резины, изменению ее динамических свойств и преждевременному разрушению образца. Это может быть при больших амплитудах, высоких частотах и длительных испытаниях.

Следовательно, динамические свойства резин не являются стабильными. При проведении стандартных динамических испытаний необходимо исключить результаты начальных циклов и результаты длительных испытаний резины.

2. Зависимость динамических свойств от амплитуды деформации.

Для ненаполненных резин наблюдается слабая зависимость динамического модуля упругости и модуля потерь от амплитуды деформации. Резины, наполненные активными наполнителями, обнаруживают сильную зависимость этих показателей от амплитуды деформации.

Динамический модуль упругости при сдвиге (G) при деформациях от 0,03 до 0,5 может быть вычислен по формуле

,

где G₀- динамический модуль упругости при сдвиге при малых значениях амплитуды деформации;

n- эмпирический коэффициент нелинейности.

Величина этого коэффициента изменяется от 0 для ненаполненных резин до 0,5 для высоконаполненных резин.

Зависимость G^II от амплитуды деформации более сложная, чем для G: в области малых амплитуд деформаций обнаруживается максимум модуля потерь при сдвиге.

3. Влияние температуры и частоты на динамические свойства.

Зависимость динамических свойств резин от частоты качественно обратна их изменению с температурой: влияние повышения частоты динамического нагружения эквивалентно влиянию понижения температуры. Частота и температура взаимозаменяемы, что следует учитывать в расчетах по прогнозированию работоспособности шин и резино-технических изделий.

Температурно-частотная эквивалентность явилась основой метода температурно-частотного приведения. В связи с тем, что определение динамических свойств резин в широком диапазоне частот вызывает экспериментальные трудности, как правило, их заменяют измерениями в широком интервале температур, что экспериментально гораздо проще.

Метод температурно-частотного приведения позволяет не только пересчитывать соответствующие температурные зависимости в частотные, но и существенно расширять диапазон охватываемых частот.

Модули G^I(или E^I) и G^II(или E^II) измерены при частоте ω и абсолютной температуре T для резины с плотностью p, могут быть преобразованы в приведенные модули и при абсолютной температуре и соответствующей плотности соотношениями:

; .

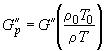Если вычертить зависимости приведенного модуля (или) от логарифма частоты при различных температурах, то они образуют семейство кривых, каждая из которых соответствует температуре. Эти кривые могут быть приведены к одной обобщенной кривой при температуре приведения путем горизонтального смещения их вдоль логарифмической оси частот на величину коэффициента приведения, данного эмпирическим уравнением Вильямса, Ландела и Ферри (ВЛФ)

,

где - температура приведения, характерная для данного полимера;

и - константы.

Уравнение ВЛФ может принимать различные формы; для применения рекомендуется следующее уравнение

,

где - температура стеклования, определяемая по ГОСТ 12254-66 или дилатометрически при скорости нагревания 0,05 °С/с.

На чертеже представлена схема построения обобщенной кривой приведенного модуля (1'-7') при температуре приведения из отдельных участков кривых (1-7), соответствующих различным температурам; кривая 4 получена при температуре. Величина определяет смещение каждой кривой (1-7) вдоль оси до кривой (1'-7') при температуре.