Элементы теории двойственности в
Пусть дана задача линейного программирования в симметричной форме записи:
(1)
Приведем определение еще одной задачи линейного программирования, тесно связанной с данной задачей.
Определение 1. Задача линейного программирования
при условиях
,
,
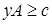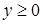где 
, называется двойственной к задаче (1).
При этом задачу (1)принятоназывать прямой.
Легко убедиться, что задача, двойственная к двойственной, является прямой задачей линейного программирования. В связи с этим часто пару задач линейного программирования: прямую и двойственную к ней называют парой взаимосопряженных задач линейного программирования.
Пусть теперь прямая задача линейного программирования записана в канонической форме:
(2)
Тогда задача двойственная к (2) определяется следующим образом:
при условиях
.
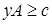Многогранную область пространства 
, определяемую ограничениями двойственной задачи, будем обозначать 
.
Запишем функции Лагранжа для прямой и двойственной задач линейного программирования:
, 
,
а также условия дополняющей нежесткости для этих задач:
и 
.
Следующие три теоремы формулируют свойства взаимосопряженных задач линейного программирования, вытекающие непосредственно из их определения.
Теорема 1. Пусть дана пара взаимосопряженных задач линейного программирования в симметричной форме, векторы 
и 
. Тогда
. (3)
Доказательство. Легко увидеть, что из ограничений прямой и двойственной задач линейного программирования следуют неравенства:
.
Из них и получаем неравенство (3).
Теорема 2. Пусть дана пара взаимосопряженных задач линейного программирования в симметричной форме, векторы 
и 
таковы, что
. (4)
Тогда векторы 
являются решениями, соответственно, прямой и двойственной задач линейного программирования.
Доказательство. Из теоремы 1 следует, что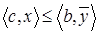 
для любого 
. Отсюда и из равенства (4) имеем 
для любого . Таким образом, 
– решение прямой задачи линейного программирования. Второе утверждение теоремы доказывается аналогично.
Теорема 3. Для того чтобы множество 
было пустым, достаточно, чтобы функция 
была неограниченна снизу на множестве .
Справедливость этого утверждения следует непосредственно из теоремы 1.
Очевидно, что утверждение Теоремы 3 в применении к двойственной задаче принимает вид:
Для того чтобы множество было пустым, достаточно, чтобы функция 
была неограниченна сверху на множестве .
Теорема 4. (Теорема двойственности). Пусть одна из пары взаимосопряженных задач линейного программирования в симметричной форме имеет решение. Тогда и двойственная к ней задача тоже имеет решение и для любых векторов 
и 
выполняется равенство
. (5)
Доказательство. Пусть имеет решение прямая задача линейного программирования. Тогда из теоремы 11.4 (теорема Кунна-Таккера в форме о седловой точке функции Лагранжа) следует, что найдется такой вектор 
, что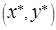 
является седловой точкой функции Лагранжа прямой задачи линейного программирования. Таким образом, 
. Отсюда и из определения функции Лагранжа следуют неравенства
Перепишем эти неравенства в следующем виде
Отсюда и из определения функции Лагранжа для двойственной задачи следуют неравенства 
. Последние неравенства означают, что вектор 
является седловой точкой функции Лагранжа для двойственной задачи. Тогда из теоремы 11.4 следует, что вектор 
– решение двойственной задачи линейного программирования.
Для доказательства второго утверждения теоремы положим и . Так как выполняются условия дополняющей нежесткости 
и 
, имеем 
. Таким образом, справедливо равенство (5). Что и требовалось.
Заметим, что все результаты этого параграфа были изложены применительно к задачам линейного программирования в симметричной форме. Аналогичные утверждения справедливы и для задач в других формах записи с небольшими изменениями, связанными только лишь с конкретной формой.
Подводя итоги полученным в этом параграфе результатам, можно сделать следующие выводы: либо обе взаимосопряженные задачи линейного программирования имеют решения, либо обе не имеют решений. При этом неограниченность целевой функции на допустимой области одной из задач возможна только в том случае, если допустимая область двойственной задачи пуста. Возможно также, что допустимые области обеих задач пусты.
Заметим, наконец, что, как следует из теорем 2 и 4, решение следующей системы:
эквивалентно решению пары взаимосопряженных задач линейного программирования. На этом факте базируются некоторые методы решения задач линейого программирования.