Процессы смешения полимера с различными добав-ками играют большую роль в технологии переработки пла-стмасс. При этом стремятся добиться равномерного распре-деления добавок по объему композиции, т.к. это обеспечи-вает однородность всех физических и химических характе-ристик материала (прочностные и деформационные показа тели, плотность, проницаемость, химическая и термическая стабильность, технологические характеристики).
Равномерность распределения компонентов характе-ризует качество смешения и зависит от суммарной деформа-ции сдвига реализуемой в процессе смешения.
Характер распределения компонентов в объеме ком-позиции можно определить методом оптической микроско-пии (при размере частиц от микрометра и выше), оценивают оптическую плотность пленок, изготовленных из компози-ций, электропроводность, а также распределение образцов композиции по плотности.
Плотности серии образцов малого размера достаточ-но точно и быстро можно определить методом флотацион-ного титрования, основанном на равенстве плотностей жид-кости и плавающего в этой жидкости образца. Если плот-ность образца больше плотности среды, то он тонет в ней и опускается на дно, если меньше – плавает на поверхности. Плотность среды можно регулировать, добавляя к исходной жидкости по каплям другую жидкость, с большей или мень-шей плотностью. Обе жидкости должны хорошо смачивать образец и быть совместимы друг с другом.
В соответствии с правилом аддитивности плотность смеси жидкостей пропорциональна их объемным долям в смеси:
(1)
где 
- плотности смеси жидкостей, плотность первой и второй жидкости;
;
.
Определив плотность гранул в достаточно широкой вы-борке из партии материала, можно построить кривую их рас-пределения по плотности, которая качественно характеризует распределение компонентов в результате смешения. Чем лучше качество смешения, тем уже распределение плотности образ-цов.
|
|
Количественно характеризовать качество смешения
можно по величине индексов смешения, расчет которых ве-дется на основе статистических параметров.
Если распределение компонентов в композиции соот-ветствует закону биномиального (идеального статистичес-кого) распределения, то генеральная дисперсия распределе-ния (σ) может быть определена по формуле:
σ 2 = q (1 – q)/ N, 
(2)
где q - доля частиц диспергируемой фазы в объеме смеси, т.е. N2 / N; а N - сумма частиц в пробе.
При анализе полимерной композиции можно предпо - ложить, что размеры частиц дисперсной фазы (например, наполнителя, стабилизатора, пластификатора или второго полимера) и «частиц» полимерной матрицы одинаковы. Тогда в каждой грануле полимерного материала при идеаль-ном смешении будет содержаться N1 частиц дисперсной фа-зы и N 2 частиц полимера (N1+ N2 = N).
Если средний размер гранул цилиндрической формы: L – длина, R – радиус, то объем гранулы Vг = πR2L, а объем каждой частицы дисперсной фазы и «частицы» полимера со-ставит Vч = π(dэкв)3/6. Общее число частиц в каждой гра-нуле N = Vu/ Vч = 6 R2L /(dэкв) 3.
При концентрации дисперсной фазы φд (объемные доли), занимаемый ею объем составит φVг или φπR2L, а число частиц дисперсной фазы в грануле N 1 = 6φR2L/(dэкв )3. Следовательно, q = φд.
Реальная дисперсия распределения находится на ос-нове оценки количества частиц дисперсной фазы в 20 - 25 образцах и рассчитывается по формуле:
|
|
(3)
где М - число образцов (гранул) в выборке, взятой для анализа;
Хi - доля диспергированного вещества в каждой грану-ле, которая численно равна φ iд.
Зная плотность гранулы, плотность полимера и плот-ность диспергированного вещества можно рассчитать его объемную долю вданной грануле из зависимости
, (4)
где 
- плотности композиции, полимера и дисперс-ной фазы; 
- объемная доля дисперсной фазы;
, (5)
а среднее значение концентрации диспергированного вещества в пробе 
(6)
Для оценки качества смеси можно использовать коэффициент вариации (в %):
, (7)
Необходимо выполнение случайности отбора проб и представительности выборки, которые контролируются от-клонением средней концентрации 
от общей концентрации компонента в смеси q. В качестве такой меры служит крите-рий значимости данного отклонения:
Z = 
Если значение Z больше табличного для оценки с заданной степенью надежности α (таблица), то отобранные пробы не удовлетворяют требуемым условиям и их надо заменить дру-гой выборкой, или принять для обработки большее число ис-пытаний.
| N - 1 | Коэффициент Стьюдента при α | ||
| 0,90 | 0,95 | 0,99 | |
| 1,81 | 2,23 | 3,17 | |
| 1,80 | 2,20 | 3,11 | |
| 1,78 | 2,18 | 3,05 | |
| 1,77 | 2,16 | 3,01 | |
| 1,76 | 2,14 | 2,98 | |
| 1,75 | 2,13 | 2,95 | |
| 1,75 | 2,12 | 2,92 | |
| 1,74 | 2,11 | 2,90 | |
| 1,73 | 2,10 | 2,88 | |
| 1,73 | 2,09 | 2,86 | |
| 1,72 | 2,09 | 2,85 | |
| 1,72 | 2,08 | 2,83 | |
| 1,72 | 2,07 | 2,82 | |
| 1,71 | 2,07 | 2,81 | |
| 1,71 | 2,06 | 2,80 | |
| 1,71 | 2,06 | 2,79 | |
| 1,71 | 2,06 | 2,78 | |
| 1,70 | 2,77 | ||
| 1,70 | 2,05 | 2,76 | |
| 1,70 | 2,05 | 2,76 | |
| 1,70 | 2,04 | 2,75 | |
| 1,68 | 2,02 | 2,70 |
Кроме того, мерой отклонения реальной смеси от со-стояния идеальных смесей могут служить следующие крите-рии:
|
|
индекс смешения I 1 = σ2/S2 (8)
критерий Лейси I 2 = (σo 2 - S 2)/(σo 2 - σ 2), (9)
где σo2 = q(1-q), т.е. генеральная дисперсия при наимень-шей пробе, когда число частиц в пробе N = 1.
Также можно рассчитать интенсивность разделения
I 3 = 
(10)
и коэффициент неоднородности
. (11)
Значения индекса смешения и критерия Лейси изме-няются от 0 до 1 при повышении качества смешения от абсо- лютно несмешенной системы до идеального (случайного) распределения компонентов. Индекс смешения и критерий Лейси показывают степень приближения качества смеси к предельно возможному состоянию случайной смеси, достигаемому при очень длительном смешении. Критерий Лейси удобно применять для оценки эффективности на стадии грубого смешения. При тонком смешении критерий теряет чувствительность и принимает значения практически равные единице.
Интенсивность разделения I 3 и коэффициент неод-нородности I 4 используют для сравнения полученной смеси с системой с однородным распределением компонентов. Их предельное значение равно нулю I 3 = I 4 = 0, но оно не достигается. Так значения показателя неоднородности I4 ограничены величиной коэффициента вариации. Поэтому, рассчитывая дисперсию плотности отобранных проб и дисперсию воспроизводимости, можно качественно оценить характер смешения и рассчитать индексы смешения.
Дисперсия воспроизводимости определения плотнос- ти проб рассчитывается как:
, (11)
где
N - общее число образцов (проб) в каждом опыте;
m - число параллельных опытов;
- среднее значение плотности образцов в каждом опыте;
- значение плотности в параллельных опытах.
Дисперсия плотности образцов рассчитывается как
, (12)
где N- число образцов в каждом опыте;
- плотность единичного образца;
- среднее значение плотности для N образцов, равное 
(13)
Цель работы: Оценка качества смешения полимерной композиции по распределению плотности образцов (гранул).
Оборудование: стакан (100 мл), мерная пипетка, мерная бюретка с ценой деления 0,1 мл, стеклянная палочка, мерный цилиндр, набор денсиметров, пинцет, титруемый раствор (ρ1) и титрующий раствор (ρ2).
Материалы: гранулы композиций на основе ПЭНП, ПЭВП, ПП с минеральными наполнителями или гранулы смесей полимеров, существенно отличающихся по плотности.
Для оценки качества смешения используются дан-ные оценки плотности не менее 25 образцов, полученные по трем параллельным замерам. Образцы (всего 75) отбира-ются случайным образом из объема композиции и делятся на три партии по 25 штук. Плотность образцов определяется методом флотационного титрования, основанном на равен-стве плотности жидкости и образца, находящемся в этой жидкости во взвешенном состоянии.
Определение плотности гранул:
В стакан с титруемой жидкостью (V1 = 50мл) поме-щаются 25 гранул, предварительно обезжиренных промыв-кой в спирте. Если плотность гранул меньше плотности жидкости в стакане, гранулы будут плавать на поверхности, а при добавлении жидкости с большей плотностью, чем на-ходящаяся в стакане, плотность смеси жидкостей будет уве-личиваться. В тот момент, когда плотность смеси жидкостей в стакане станет равной плотности гранулы, эта гранула опустится с поверхности. В том случае, когда плотность гранул выше, чем плотность жидкости, находящейся в ста-кане, они будут находиться на дне стакана. При выравни-вании плотности гранулы с плотностью смеси жидкостей, всплывýт.
Из мерной бюретки по каплям при перемешивании приливается в стакан титрующая жидкость до всплытия первой гранулы. Фиксируется количество титрующей жид-кости, затраченной на титрование, и количество всплывших гранул. Всплывшие гранулы вынимаются из стакана пин-цетом. Титрование ведется до всплытия последнего образца. Определение повторяется три раза (число параллельных опытов).
В протокол испытаний вносится:
- исходный объем титруемой жидкости (V1);
- плотности титруемой и титрующей жидкостей (ρ 1 и ρ 2);
- количество всплывших (утонувших) образцов (N i);
- количество титрующей жидкости, прилитой к моменту всплытия i-того образца; (V i).
Плотность образцов рассчитывается по формуле:
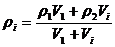, (10)
Результаты расчета плотности вносятся в протокол испытаний.
На основании полученных результатов строится кривая распределения плотности образцов в координатах «% всплыв-ших образцов – плотность» или «% утонувших образцов – плот-ность». Рекомендуемый интервал на шкале плотности 0,01кг/м3.
Таблица записи опытных данных:
| № п\п | Объем титруемой жидкости, (V1),см3 | Плотность титруемого раствора, (ρ 1), г /см3 | Плотность титрующей жидкости, (ρ 2), г/см3 | Число всплывших (утонувших) образцов (Ni) | Объем прилитой жидкости, см3 | Плотность всплывших (утонувших) образцов, (ρ i), г/см3 | |
1 На основании полученных результатов 3-х параллельных опытов построить кривые распределения плотности образ-цов в координатах «% всплывших образцов – плотность» или «% утонувших образцов – плотность». Путем графи-ческого усреднения найти вид кривой распределения плот-ности образцов данной композиции и качественно оценить степень смешения.
2. Рассчитать коэффициент вариации распределения плот-ности образцов исследованной композиции,
3. Рассчитать индексы смешения. По их величине оценить качество исследованных композиций.
Вопросы к лабораторной работе:
1 В чем состоит сущность процесса ламинарного смешения?
2 В чем состоит сущность процесса диспергирующего смешения?
3 Как осуществляется смешение с малым количеством добавок?
4. Как осуществляется введение пластификаторов вполимеры?
5 Основные закономерности смешения полимеров, связь размера частиц дисперсной фазы с реологическими свойствами компонентов.
6. Какие статистические критерии используются для оценки качества смешения?
7. Какие основные виды смесительного оборудования откры –того и закрытого типов Вы знаете? Приведите принципиаль-ные схемы этих устройств.
8 Приведите технологические схемы получения композиций с дисперсным наполнителем, с волокнистым наполнителем.
9 Какие методы используются для оценки распределения компонентов в объеме композиции?
10 Какие факторы в ходе определения плотности образцов могут привести к искажению результатов?
11 Какое влияние на качество смешения оказывает порядок введения компонентов композиции?
12. Имеется ли корреляция между качеством смешения и уровнем физико-механических показателей композиции?
Литература:
1 Основы технологии переработки пластмасс / Под ред. В.Н. Кулезнева и В.К Гусева - М.: Химия, 2006. – С.118 – 145.
2 Торнер Р.В. Теоретические основы переработки
полимеров - М., Химия, 1977. - С. 202-231.
3. Тадмор З., Гогос К. Теоретические основы переработки полимеров. Пер. с англ. – М.: Химия, 1984. – С.181 – 213.
4. Техника переработки пластмасс. / Под ред. Н.И. Басова и В. Броя – М.: Химия, 1985. – С. 79 - 114.
5 Богданов В.В. Смешение полимеров. - Л.: Химия, 1982. – 109 с.
Издание учебное
Ушакова Ольга Борисовна