Задачи для самостоятельного решения

1.1. По формуле % рассчитайте верхнюю и нижнюю гра­ни­цы y _max и y _min по­ля допуска радиокомпонентов с номинальными значениями параметров y _н=10⁴ ± 10%, y _н=510×10^–12 ± 20%, y _н=3,2×10 ⁹ ± 5%.

1.2. Для значений y _max и y _min , полученных в предыдущем примере, рассчитать и занести в таблицу число интервалов k и ширину интервала D k для построения гистограммы при различных объемах N выборки радиокомпонентов:

N
k
D k

Построить график зависимости k = f (N).

1.3. Построить гистограмму распределения емкости выборки конденсаторов объема N =20 со значениями емкостей, приведенными в таблице Рассчитать среднее значение и величину среднеквадратического отклонения емкости конденсаторов.

Значения емкостей выборки конденсаторов с С_н=1500 пФ±10%

1.4. Построить десятичный ряд предпочтительных чисел Е12. Доказать, что предельное отклонение значений членов ряда не превышают 10%.

1.5. Построить десятичный ряд предпочтительных чисел Е24. Доказать, что предельное отклонение значений членов ряда не превышают 5%.

1.6. Выведите формулу (1.9) для расчета относительного от­кло­не­­ния выходного параметра у методом наихудшего случая. Дайте оп­­ре­­де­ления коэффициентов влияния А_i и В_i.

1.7. Докажите на примере, что если выходной параметр y представлен функцией вида

,

то относительные коэффициенты влияния при входных параметрах x_i находятся по формуле

B_i=n_i.

 

1.8. Докажите на примере, что если выходной параметр y представлен дробно-рациональной функцией вида

,

то относительные коэффициенты влияния при входных параметрах x_i находятся по формуле

.

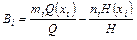(В качестве примера воспользуйтесь формулой для индуктивности катушки с броневым сердечником:

, Гн,

где А – постоянная величина; m_н – начальная магнитная проницаемость материала сердечника; l _c – длина магнитной силовой линии, см; l _з – величина зазора между половинками сердечника, см.).

1.9. Выведите формулу (1.10) для расчета температурного коэф­фи­­ци­ента выходного параметра.

1.10. Выведите выражение (1.12) для расчета относительного сред­­не­квадра­ти­че­ского отклонения выходного параметра.

1.11. С использованием метода наихудшего случая выведите формулы для расчета от­­кло­не­ний выходных параметров у, задан­ных сле­ду­ю­щи­ми фун­кциями:

а) ; б) ; в) .

1.12. С использованием вероятностно-статистического метода рас­­счи­тай­те отклонения выходных параметров, заданных фор­му­ла­ми а), б), в) п. 1.6.

1.13. Сопротивление проволочного резистора рассчитывается по формуле:

, Ом,

где r - удельное сопротивление провода, Ом мм²/м; l _пр – длина намоточного провода; d ₀ – диаметр провода без изоляции, мм.

Вывести выражение для расчета производственной погрешности и температурного коэффициента сопротивления резистора.

1.14. Определить длину нихромовой проволоки диаметром 0,5 мм, используемой для изготовления нагревательного устройства с сопротивлением 20 Ом при температуре 1000 ^оС, полагая, что при 20 ^оС параметры нихрома следующие:

1) удельное сопротивление ρ = 1,0 мкОм·м;

2) температурный коэффициент удельного сопротивления (ТК _ρ) α_{ρ, Т} =-1,5·10^-4 К^-1;

3) температурный коэффициент линейного расширения (ТКЛР) α _l =-1,5·10^-5 К^-1.

1.15. Сопротивление провода из константана при 20^оС равно 500 Ом. Определить сопротивление этого провода при 450^оС, если при 20^оС ТК _ρ константана α_{ρ, Т} =-15·10^-6 К^-1, а ТКЛР составляет 10^-5 К^-1.

1.16. Сопротивление вольфрамовой нити электрической лампочки при 20^оС равно 35 Ом. Определить температуру нити лампочки, если известно, что при ее включении в сеть напряжением 220 В в установившемся режиме по нити проходит ток 0,6 А. ТК _ρ вольфрама при 20^оС α_{ρ, Т} =5·10^-3 К^-1.

1.17. Стержень из графита соединен последовательно с медным стержнем того же сечения. Определить, при каком отношении длин стержней сопротивление этой композиции не зависит от температуры. Удельные сопротивления меди и графита равны, соответственно 0,017 и 8,0 мкОм·м, а значения α_{ρ, Т} для этих материалов составляют 4,3·10^-3 и –10^-3 К^-1.

1.18. Одинаковым ли будет относительное изменение удельного сопротивления меди для двух температурных интервалов: 20 – 60 ^оС и 60 – 100 ^оС (по отношению к начальному значению в каждом из этих интервалов)?

1.19. Удельное сопротивление чистой меди при 20 и 100 ^оС равно соответственно 0,0168 и 0,0226 мкОм·м. Пользуясь линейной аппроксимацией зависимости ρ(Т), определить температурный коэффициент сопротивления при ^оС.

1.20. Доказать, что между температурным коэффициентом сопротивления проводника α _{R , Т} , удельного сопротивления материала α_{ρ, Т} и линейного расширения α _{l , Т} существует следующая взаимосвязь: α_{ρ, Т} =α _{R , Т} +α _{l , Т} .

1.21. Определить температурный коэффициент линейного расширения α _{l , Т} и удлинение нихромовой проволоки, если известно, что при повышении температуры от 20 до 1000 ^оС электрическое сопротивление проволоки изменяется от 50 до 56,6 Ом. Длина проволоки в холодном состоянии l =50 м. Температурный коэффициент удельного сопротивления нихрома принять равным 15·10^-5 К^-1.

1.22. При нагревании провода из манганина длиной 1,5 м и диаметром 0,1 мм от 20 до 100 ^оС его сопротивление уменьшается на 0,07 Ом, а длина возрастает на 0,16 %. Определить температурный коэффициент удельного сопротивления. При расчетах принять, что при комнатной температуре для манганина удельное сопротивление ρ=0,47 мкОм·м.

1.23. Емкость трубчатого конденсатора в виде двух коаксиальных проводящих цилиндров, разделенных диэлектриком, равна

, Ф,

где l – длина перекрытия обкладок, м; D ₁ и D ₂ – внутренний и наружный диаметры изоляционного основания (про­к­лад­ки).

Вывести выражение для расчета производственной погрешности и температурного коэффициента емкости конденсатора.

1.24. Удельное электросопротивление диэлектрика изменяется с температурой по экспоненциальному закону: ρ=Аеxp(α_{ρ, Т} / Т), где А – постоянная, Т – абсолютная температура, К.

При изменении температуры от 60 до 127 ^оС удельное сопротивление радиофарфора уменьшается от ρ₁=10¹³ Ом·м до ρ₂=10¹¹ Ом·м. Определить ТК _ρ радиофарфора, считая его постоянным в рассматриваемом диапазоне температур. При этом же допущении найти удельное сопротивление ρ материала при комнатной температуре.

1.25. В комбинированном пленочном конденсаторе спиральной конструкции для получения высокой температурной стабильности емкости совместно используют диэлектрические пленки двух различных полимеров, имеющих разные знаки температурного коэффициента диэлектрической проницаемости (ТК _ε) α_{ε, Т} . Конструкция конденсатора содержит полистирольную и поликарбонатную пленки толщины h ₁ и h ₂, соответственно. Емкости двух диэлектрических лент С ₁ и С ₂ включены параллельно, общая емкость конденсатора С = С ₁+ С ₂. Определить, при каком отношении толщин пленок температурный коэффициент емкости α _С,Т близок нулю. Учесть, что температурные изменения емкостей лент обусловлены в основном температурными изменениями диэлектрических проницаемостей ε₁ и ε₂.

1.26. Керамический конденсатор емкостью 1,5 нФ при комнатной температуре имеет температурный коэффициент емкости α _С,Т =-750·10^-6 К^-1. Графически показать температурную зависимость емкости этого конденсатора. Чему будет равна его емкость при температуре Т =-40 ^оС?

1.27. Емкость слюдяного металлизированного конденсатора c плоскими обкладками рассчитывается по формуле С = ε_оε(n -1) S / d, где n - число обкладок, S –площадь обкладки, d - толщина слюдяного диэлектрика.

Пусть значение емкости составляет 200 пФ при 20 ^оС. Чему будет равна емкость этого конденсатора при 100 ^оС, если ТК _ε слюды принять равным 50·10^-6 К^-1, а ее ТКЛР – равным 14·10^-6 К^-1.

1.28.Рассчитать производственные допуски на элементы конструкции и материалы катушки с сердечником при следующих исходных данных:

1) индуктивность L =100мкГ %;

2) размеры катушки – диаметр D _к = 5 мм, длина l = 9 мм;

3) число витков катушки N =17,3;

4) начальная магнитная проницаемость сердечника m_н = 700 150.

1.29.Рассчитать производственные допуски на элементы конструкции и материалы катушки с сердечником при следующих исходных данных:

1) индуктивность L =35мкГ %;

2) размеры катушки – диаметр D _к = 4 мм, длина l = 7 мм;

3) число витков катушки N =22;

4) начальная магнитная проницаемость сердечника m_н = 400 150.

1.30. Формула для резонансной частоты колебательного контура имеет вид:

, Гц,

где L – индуктивность контурной катушки, Гн; C - емкость контурной конденсатора колебательного контура, Ф.

С использованием метода наихудшего случая и вероятностно-статистического метода вывести выражение для расчета производственной погрешности и температурного коэффициента резонансной частоты.

1.31.Рассчитать производственную погрешность d L _c индуктивности катушки с броневым сердечником при следующих исходных данных:

1) броневой сердечник типо­размера Б9;

2) габа­ри­тные размеры сердечника:

наружный диаметр D ₁ = 9,3 мм,

внутренний диаметр D ₂ = 7,5 мм,

диаметр центрального керна D ₃ = 3,9 мм,

высота сердечника H ₁ = 5,4 мм,

высота окна H ₂ = 3,6 мм;

3) начальная магнитная проницаемость сердечника m_н = 50 18%;

4) относительная маг­нит­­ная проницаемость сердечника m_отн = 26,2.

5) величина зазора между чашками l _з = 0,2 мм 30%.

1.32.Рассчитать температурный коэффициент индуктивности (ТКИ) и оценить значения индуктивности катушки с цилиндрическим сердечником в заданном диапазоне температур при следующих исходных данных:

1) индуктивность L =100мкГ %;

2) материал сердечника - феррит 700НМ;

3) начальная магнитная проницаемость сердечника m_н = 700;

4) ТК m=a_{m, T} = (–1,4...+8,4)×10^–4 К^–1;

5) ТКЛР материла каркаса катушки a _D,T 0,1×10^–4 1/К;

6) диапазон температур эксплуатации (–40¼+40) °С.

1.33.Рассчитать температурный коэффициент индуктивности (ТКИ) и оценить значения индуктивности катушки с цилиндрическим сердечником в заданном диапазоне температур при следующих исходных данных:

1) индуктивность L =15мкГ %;

2) материал сердечника - феррит 100НН;

3) начальная магнитная проницаемость сердечника m_н = 100;

4) ТК m=a_{m, T} = (0,5...4,5)×10^–4 К^–1;

5) ТКЛР материла каркаса катушки a _D,T 0,15×10^–4 1/К;

6) диапазон температур эксплуатации (–40¼+70) °С.

1.34.Рассчитать температурный коэффициент индуктивности (ТКИ) и оценить значения индуктивности катушки на кольцевом сердечнике в заданном диапазоне температур при следующих исходных данных:

1) индуктивность L = 15 0,5 мкГ;

2) материал сердечника - феррит 60НH;

3) ТК μ = (0,5...1,5)10^–4 К^–1.

4) рабочий диапазон температур катушки –60¼+50 °C

1.35.Рассчитать производственную погрешность емкости дискретного конденсатора с параллельным включением конденсаторов по схеме рис. 3.6 при следующих исходных данных:

1) количество ветвей n =3;

2) значения емкостей конденсаторов, включенных в ветви:

С1 =1 пФ±0,25%; С2 =2,2 пФ±0,25%; С3 =4,7 пФ±0,25%;

3) коэффициент перекрытия контура по частоте k_f =1,2;

4) максимальное значение эквивалентной емкости C_{э. max}=67 пФ;

1.36.Рассчитать производственную погрешность линейных размеров d l пластины ротора и статора, зазора d d между обкладками, ТКЕ (a _С,T)и температурную нестабильность емкости КПЕ при следующих исходных данных:

1) предельно допустимое отклонение емкости не более d С 5%.;

2) зазор между пластинами ротора и статора d = 0,5 мм;

3) средний размер пластины ротора и статора 20 мм

4) материал обкладки - алюминий с ТКЛР = 0,26×10^–4 К^–1;

5) диапазон температур эксплуатации (–60¼+40 °С).

1.37.Рассчитать температурный коэффициент емкости (a _С,T)и температурную нестабильность емкости КПЕ при следующих исходных данных:

1) зазор между пластинами ротора и статора d = 0,5 мм;

2) средний размер пластины ротора и статора 20 мм

3) материал обкладки - алюминий с ТКЛР = 0,26×10^–4 К^–1;

4) диапазон температур эксплуатации (–60¼+65 °С).

1.38. Формула для температуры перегрева D T трансформатора питания малой мощности имеет вид:

, К,

где А и Б –постоянные коэффициенты, К/Вт; P _м и P _c – соответственно, потери в меди и в стали, Вт/кг.

Вывести выражение для расчета относительной производственной погрешности v (D T) температуры перегрева трансформатора.

1.39. Рассчитать ТКС проволочного резистора, а также диапазон изменения сопротивления резистора в заданном диапазоне температур. Исходные данные для расчета:

1) номинальное сопротивление R _н = 56 кОм 5%;

2) температурный диапазон работы –45¼+70 °C;

3) ТКС материала провода (сплав Х20Н80) a_{r, T} = +0,9×10^–4 1/К.

4) ТКЛР обмоточного провода a _d,T = +0,14×10^–4 1/К;

5) ТКЛР материала каркаса a _D,T = +0,12×10^–4 1/К.