1. Найти пределы функций, не пользуясь правилом Лопиталя.
2. Найти производную функций.
3. Исследовать функцию f(x) и построить график.
4. Найти частные производные первого порядка функции Z = f(x, y) двух независимых переменных х, y.
5. Найти неопределенные интегралы.
6. Вычислить площадь фигуры, ограниченной графиками функций f(x) и g(x).
7. Найти частное решение дифференциального уравнения, удовлетворяющее указанному начальному условию.
8. Найти частное решение дифференциального уравнения второго порядка, удовлетворяющее указанным начальным условиям.
9. Исследовать ряд на сходимость.
10. Найти радиус и интервал сходимости степенного ряда.
Вариант 0
1. а)  б)
б) 

2. а)  б)
б) 
3.  4.
4. 
5. а)  б)
б) 
6. 
7. 
8. 
9.  10.
10. 
Вариант 1
1. а)  б)
б) 
2. а)  б)
б) 
3.  4.
4. 
5. а)  б)
б) 
6. 
7. 
8. 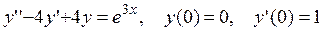
9.  10.
10. 
Вариант 2
1. а) 
 б)
б) 


2. а) 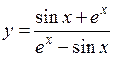 б)
б) 
3.  4.
4. 
5. а)  б)
б) 
6. 
7. 
8. 
9.  10.
10. 
Вариант 3
1. а) 
 б)
б) 
2. а)  б)
б) 
3.  4.
4. 
5. а)  б)
б) 
6. 
7. 
8. 
9.  10.
10. 
Вариант 4
1. а) 
 б)
б) 
2. а) 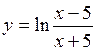 б)
б) 
3.  4.
4. 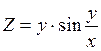
5. а)  б)
б) 
6. 
7. 
8. 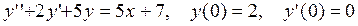
9.  10.
10. 
Вариант 5
1. а)  б)
б) 
2. а)  б)
б) 
3.  4.
4. 
5. а)  б)
б) 
6. 
7. 
8. 
9.  10.
10. 
Вариант 6
1. а)  б)
б) 
2. а)  б)
б) 
3.  4.
4. 
5. а)  б)
б) 
6. 
7. 
8. 
9.  10.
10. 
Вариант 7
1. а)  б)
б) 
2. а)  б)
б) 
3.  4.
4. 
5. а)  б)
б) 
6. 
7. 
8. 
9.  10.
10. 
Вариант 8
1. а)  б)
б) 

2. а)  б)
б) 
3.  4.
4. 
5. а)  б)
б) 
6. 
7. 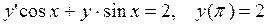
8. 
9.  10.
10. 
Вариант 9
1. а)  б)
б) 
2. а)  б)
б) 
3.  4.
4. 
5. а)  б)
б) 
6. 
7. 
8. 
9. 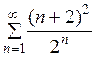 10.
10. 
3. Методические рекомендации
к выполнению контрольной работы №2
Для выполнения заданий необходимо, прежде всего, изучить методическую разработку автора из п.5 – методическое обеспечение.
Далее рекомендуется просматривать соответствующие разделы из любого пособия под редакцией Кремера Н.Ш. (электронные варианты пособий представлены в локальной сети филиала (на PABе: в материалах для студентов, в папке с фамилией лектора).
Печатные издания литературы, представленные в п.4, имеются в библиотеке филиала и могут быть использованы для решения задач.
Приведем решения некоторых задач типового варианта контрольной работы №2.
Задание 1. Найти пределы функций, не пользуясь правилом Лопиталя
а) 
Анализ
Так как для данных дробей степень числителя больше степени знаменателя, то
 и
и 
Получаем неопределенность 
Следовательно, теоремой о пределе разности воспользоваться нельзя. Необходимо провести тождественные преобразования выражения, находящегося под знаком предела.
Решение
Приведем выражение под знаком предела к общему знаменателю:

Значение дроби не изменяется, если её числитель и знаменатель разделить на одно и то же ненулевое выражение. Разделим на  .
.
Следовательно, 
Ответ: 3
б) 
Анализ
Непосредственное применение теоремы о пределе частного невозможно, поскольку
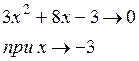 и
и 
Рассматриваемый предел представляет собой неопределенность вида  , надо освободиться от этой неопределенности. Для этого требуется провести тождественные преобразования выражения, находящегося под знаком предела.
, надо освободиться от этой неопределенности. Для этого требуется провести тождественные преобразования выражения, находящегося под знаком предела.
Решение
Если  – корни квадратного трёхчлена
– корни квадратного трёхчлена  то
то 
Найдём корни квадратного уравнения


где  - дискриминант,
- дискриминант, 

Отсюда, 
Аналогично, 
Преобразуем выражение, находящееся под знаком предела:

Использовали непрерывность функции
 в точке
в точке  т.е.
т.е. 
Ответ: 10
Задание 2. Найти производную функций
а) 
Решение
Задана сложная функция  , где
, где  .
.
Найдем  , применяя правило:
, применяя правило: 


Ответ: 
б) 
Анализ
Функция  представляет собой произведение трех функций
представляет собой произведение трех функций 

Решение
 Ответ:
Ответ: 