а) 
Решение
Преобразуем подынтегральную функцию 
Применим вначале метод замены переменной:
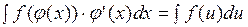 (*)
(*)

 – неправильная рациональная дробь
– неправильная рациональная дробь
Выделим целую часть, для этого выполним следующие преобразования:
 Использовали формулы таблицы интегралов:
Использовали формулы таблицы интегралов:


Ответ: 
б) 
Решение
Воспользуемся формулой интегрирования по частям:

Примем за 

Найдем дифференциал функции u:

По dv найдем функцию v: 
 (одна из первообразных; постоянную «с » не прибавляем)
(одна из первообразных; постоянную «с » не прибавляем)
Итак,  Полученный интеграл
Полученный интеграл  найдем, применяя метод замены переменной (формула (*))
найдем, применяя метод замены переменной (формула (*))
 Применили формулу таблицы основных интегралов
Применили формулу таблицы основных интегралов

Итак,
 Ответ:
Ответ: 
Задание 6. Вычислить площадь фигуры ограниченной графиками функций  и
и 
Решение
Изобразим фигуру, площадь которой надо найти, на координатной плоскости. Графиком функции g(x) является парабола, ветви которой направлены вверх. Найдем производную функции  . Находим координаты вершины параболы С:
. Находим координаты вершины параболы С:

Точки пересечения параболы с осями координат:
С осью ох: 
 ;
;
 ;
; 
C осью о у: х=0; 

Графиком функции  является прямая, которую можно построить по двум точкам с координатами
является прямая, которую можно построить по двум точкам с координатами 

Рисунок 2 – К задаче №6
Найдем точки пересечения графиков функций





 ;
; 
Площадь S фигуры ABC, ограниченной графиками функций, находим по формуле  .
.
Где  для всех
для всех 
Так как  при
при  , то
, то
 Ответ
Ответ 
Задание 7. Найти частное  решение дифференциального уравнения
решение дифференциального уравнения  , удовлетворяющее начальному условию:
, удовлетворяющее начальному условию: 
Решение
1) Разделим обе части уравнения на 
 - линейное неоднородное дифференциальное уравнение первого порядка, общий вид которого
- линейное неоднородное дифференциальное уравнение первого порядка, общий вид которого 
Общее решение данного уравнения найдем в виде  – неизвестные дифференцируемые функции которые надо найти.
– неизвестные дифференцируемые функции которые надо найти.
2) 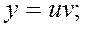
 , получаем уравнение:
, получаем уравнение:
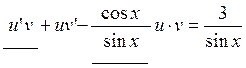 ;
; 
 (*)
(*)
3) Найдем какую-нибудь функцию u, для которой выполняется равенство  - дифференциальное уравнение первого порядка с разделяющимися переменными.
- дифференциальное уравнение первого порядка с разделяющимися переменными. 
|
|
 , разделим переменные
, разделим переменные 
Найдем неопределенные интегралы от обеих частей равенства:

 , так как
, так как 
 , полагаем с =0 (так как надо найти одну из функций u). Следовательно
, полагаем с =0 (так как надо найти одну из функций u). Следовательно 
4) Подставим 
 в уравнение
в уравнение 
 ;
;  ;
;  - разделим переменные
- разделим переменные
 , интегрируем обе части равенства:
, интегрируем обе части равенства: 
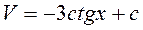
Общее решение данного дифференциального уравнения имеет вид:
 .Итак,
.Итак, 
5) Для отыскания частного решения необходимо и достаточно определить значения постоянной с по начальному условию, данному в задании.
 при
при  , получаем равенство
, получаем равенство
 , так как
, так как  , то
, то  .
.
Следовательно, 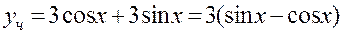
Ответ: 
Задание 8. Найти частное решение дифференциального уравнения второго порядка  , удовлетворяющее начальным условиям
, удовлетворяющее начальным условиям 
Решение
1) Составим характеристическое уравнение линейного однородного дифференциального уравнения второго порядка с постоянными коэффициента вида (ЛОДУ): 
Характеристическое уравнение: 

Характеристическое уравнение имеет комплексно-сопряженные корни. 

 - мнимая единица
- мнимая единица
Общее решение ЛОДУ: 
2) Так как правая часть данного линейного неоднородного дифференциального уравнения второго порядка с постоянными коэффициентами (ЛНДУ) имеет вид  – многочлен второй степени, еах показательная функция отсутствует, то есть а =0 – не является корнем характеристического уравнения, составленного выше, то частное решение ЛНДУ будем искать в виде многочлена второй степени с неизвестными коэффициентами:
– многочлен второй степени, еах показательная функция отсутствует, то есть а =0 – не является корнем характеристического уравнения, составленного выше, то частное решение ЛНДУ будем искать в виде многочлена второй степени с неизвестными коэффициентами:
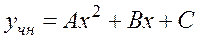


Подставим  в данное ЛНДУ уравнение:
в данное ЛНДУ уравнение:

Два многочлена равны тогда и только тогда, когда равны коэффициенты при одинаковых степенях x, находим:
|
|



Отсюда 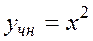 , поэтому общее решение ЛНДУ имеет вид
, поэтому общее решение ЛНДУ имеет вид

3) Находим частное решение ЛНДУ, удовлетворяющее начальным условиям, данным в задании:
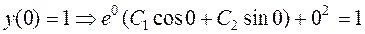




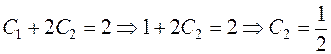
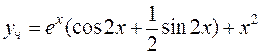
Ответ: 
Задание 9. Исследовать ряд на сходимость 
Напомним, что число n! (читается «эн-факториал» – это произведение всех натуральных чисел от единицы до n:
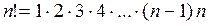
При вычислениях с факториалами представляется важными следующие соображения:


 и т.д.
и т.д.
Признак Даламбера. Если существует предел  , то числовой ряд
, то числовой ряд  сходится при q <1, и расходится при q >1.
сходится при q <1, и расходится при q >1.
Решение
 , найдем
, найдем 
Составим отношение:  следовательно, по признаку Даламбера данный ряд сходится.
следовательно, по признаку Даламбера данный ряд сходится.
Ответ: ряд сходится
Задание 10. Найти радиус и интервал сходимости степенного ряда 
Решение
Каждый степенной ряд  сходится внутри интервала
сходится внутри интервала
 - радиус сходимости, определяемый по формуле
- радиус сходимости, определяемый по формуле  , 0!=1 и 1!=1
, 0!=1 и 1!=1
Определяем радиус сходимости данного степенного ряда.

 Так как
Так как  то
то 

Интервал сходимости (-1; 7)
Ответ: R =4; (-1; 7)
Литература
Основная
1. Высшая математика для экономического бакалавриата: учебник и практикум / под ред. Н.Ш. Кремера. – М.: Юрайт, 2012.
2. Орел О.Е. Математический анализ: учеб. пособие. Ч. 1. Введение в анализ: учеб. пособие / под ред. В.Б. Гисина, Е.Н. Орла. – М.: Фин. ун-т, 2013.
3. Кремер Н.Ш. Математический анализ: Учебник и практикум / Финуниверситет; Под ред. Н.Ш.Кремера. – М.: Юрайт,2014.
4. Кремер, Н.Ш. Высшая математика для экономистов: учебник / Н.Ш. Кремер, Б.А. Путко, И.М. Тришин, М.Н. Фридман; под ред. проф. Н.Ш. Кремера – 3-е изд. – М.: ЮНИТИ – ДАНА, 2007. – 479 с.
|
|
5. Математика в экономике: учебник: В 2 ч. Ч.2. Математический анализ / А.С.Солодовников, В.А. Бабайцев, А.В. Браилов. – М.: Финансы и статистика, 2005.
Дополнительная
6. Высшая математика для экономистов: практикум для студентов вузов, обучающихся по экономическим специальностям. 2-е изд., перераб. и доп./ Н.Ш. Кремер и др.; под ред. проф. Н.Ш. Кремера – М.: ЮНИТИ-ДАНА, 2007. – 423с.
7. Коваленко Е.В. Сборник задач и тестов для совершенствования необходимых навыков по дисциплинам «Линейная алгебра и «Математический анализ». Учебно-методическое пособие для студентов по математике, программа подготовки бакалавров. М.: Фин. ун-т. Кафедра «Прикладная математика», 2014.
8. Липагина Л.В. Математический анализ: учеб. пособие. Ч.2. Дифференциальное исчисление функции одной переменной / под ред. В.Б. Гисина, Е.Н. Орла. – М.: Фин. ун-т, 2013.
9. Борцова Т.В. Математический анализ: учеб. пособие. Ч.3. Интегральное исчисление / под ред. В.Б. Гисина, Е.Н. Орла. – М.: Фин. ун-т, 2013.
10. Ягодовский П.В. Математический анализ: учеб. пособие. Ч.4. Функции нескольких переменных / под ред. В.Б. Гисина, Е.Н. Орла. – М.:Фин. ун-т, 2013.
11. Гончаренко В.М. Математический анализ: учеб. пособие. Ч.5-6. Ряды. Дифференциальные уравнения / под ред. В.Б. Гисина, Е.Н. Орла. – М.:Фин. ун-т, 2013.