для самостоятельной работы

для самостоятельной работы

по дисциплине «Математические методы исследования операций»

 

для студентов специальности

«Информационные управляющие системы и технологии»

 

Утверждено

на заседании кафедры автоматизированных систем обработки информации и управления Протокол № 1 от 29.08.2012

 

 

Киев 2012

Симплекс-метод. Методические указания для самостоятельной работы по дис­циплине «Математические методы исследования операций» для студентов специальности «Информационные управляющие системы и технологии» / Сост.: Е.Г. Жданова. – К.: НТУУ “КПИ”, 2012. – 70 с.

 

Учебное издание

Симплекс-метод

 

МетодичЕСКИЕ УКАЗАНИЯ

для самостоятельной работы

по дисциплине «Математические методы исследования операций»

 

для студентов специальности

«Информационные управляющие системы и технологии»

 

 

Составитель Жданова Елена Григорьевна

 

Ответственный редактор В.А. Тихонов

Рецензенты: C.Ф. Теленик

В.Н. Кузнецов

Методические указания содержат теоретические основы симплекс-метода – основного метода решения задач линейного программирования. Приведены основные теоремы линейного программирования, схемы алгоритмов симплекс-метода и табличного симплекс-метода. Рассмотрены методы нахождения начального допустимого базисного решения, особые случаи использования симплекс-метода. Приведены примеры решения задач линейного программирования и задания для контрольных работ.

 

 

Содержание

1. Формы ЗЛП................................................................................................................................... 4

2. Эквивалентность различных форм ЗЛП............................................................................. 5

3. Основные свойства ЗЛП.......................................................................................................... 8

4. Идея симплекс – метода......................................................................................................... 12

5. Преобразованная задача....................................................................................................... 12

6. Способ перехода от одного ДБР к другому....................................................................... 14

7. Условие оптимальности ДБР................................................................................................ 16

8. Схема симплекс-метода......................................................................................................... 18

9. Табличный симплекс-метод.................................................................................................. 21

9.1. Схема табличного симплекс-метода...................................................................... 22

10. Примеры реализации табличного симплекс-метода................................................... 23

11. Искусственное начальное решение.................................................................................. 34

11.1. М - метод...................................................................................................................... 35

11.2. Двухэтапный метод................................................................................................... 38

12. Вырожденность....................................................................................................................... 46

12.1 Вырожденное оптимальное решение................................................................... 46

12.2. Промежуточное вырожденное решение............................................................. 48

13. Альтернативные оптимальные решения........................................................................ 56

14. Неограниченность пространства решений и целевой функции............................... 59

15. Отсутствие допустимых решений..................................................................................... 63

16.Задания для контрольной работы...................................................................................... 68

Список литературы...................................................................................................................... 70

 

1. Формы ЗЛП

Задача математического программирования вида:

называется задачей линейного программирования (ЗЛП).

Основными допущениями, принимаемыми при построении линейных моделей, является пропорцио­нальность, аддитивность, неотрицательность.

В зависимости от вида ограничений различают три основные формы ЗЛП.

ЗЛП вида (1)–(5) называется общей ЗЛП.

ЗЛП вида:

называется стандартной ЗЛП. В матричном виде она записывается следующим образом:

где

ЗЛП вида:

называется канонической ЗЛП. Она может быть записана в матричном виде следующим образом:

Метод решения ЗЛП разработан для задачи в канонической форме.

 

2. Эквивалентность различных форм ЗЛП

Все перечисленные формы ЗЛП являются эквивалентными в том смысле, что простыми преобразова­ниями задачу, имеющую одну из форм, легко привести к задаче, имеющей одну из оставшихся форм, причем по оптимальному решению построенной задачи легко найти оптимальное решение исходной задачи. Следо­вательно, различные формы ЗЛП по существу являются различными формами записи ЗЛП.

Правила преобразования различных форм ЗЛП:

а) максимизация целевой функции эквивалентна минимизации целевой функции ;

б) ограничение-неравенство «≤» с помощью введения неотрицательной переменной можно заменить системой:

где s_i – остаточная переменная;

в) ограничение-неравенство «≥» с помощью введения неотрицательной переменной можно заменить сис­темой:

где s_i – избыточная переменная.

Остаточные и избыточные переменные называются еще свободными, балансовыми, дополнительны­ми;

г) ограничение-равенство можно заменить двумя неравенствами:

д) неравенство «≥» переводится в неравенство «≤» умножением его на –1.

е) m ограничений-равенств можно заменить на (m+1) неравенство:

ж) если на x_j не накладывается ограничение не отрицательности, то, введя новые две неотрицатель­ные переменные x_j⁺≥0, x_j^–≥0, исходную переменную x_j можно исключить путем замены: x_j=x_j⁺–x_j^–. Следовательно, всегда найдутся такие неотрицательные x_j⁺, x_j^–, что их разность даст x_j.

 

Пример 2.1

Привести ЗЛП к канонической форме:

z = 3x₁ – x₂ → max,

x₁ + 2x₂ ≥ 6,

– 2x₁ + 7x₂ ≥ 8,

3x₁ – 8x₂ ≤ 15,

– 4x₁ + x₂ = 10,

x₁, x₂ ≥ 0.

Решение

Так как первое ограничение имеет знак “≥”, то в левую часть ограничения вводим избыточную переменную s₁. Данное ограничение будет иметь вид:

x₁ + 2x₂ – s₁ = 6,

s₁ ≥ 0.

 

Второе ограничение также имеет знак “≥”, для приведения к канонической форме в левую часть ограничения вводим избыточную переменную s₂:

– 2x₁ + 7x₂ – s₂ = 8,

s₂ ≥ 0.

 

Так как третье ограничение имеет знак “≤”, то в левую часть ограничения добавляем остаточную переменную s₃:

3x₁ – 8x₂ + s₃ = 15,

s₃ ≥ 0.

 

Так как четвёртое ограничение имеет знак “=”, то ограничение оставляем без изменения, не добавляя дополнительных переменных. Данное ограничение в канонической форме имеет исходный вид:

-4x₁ + x₂ = 10.

 

Итак, в канонической форме данная ЗЛП будет выглядеть так:

z = 3x₁ – x₂ + 0s₁ + 0s₂ + 0s₃ → max

x₁ + 2x₂ – s₁ = 6,

–2x₁ + 7x₂ – s₂ = 8,

3x₁ – 8x₂ + s₃ = 15,

–4x₁ + x₂ = 10,

x₁, x₂, s₁, s₂, s₃ ≥ 0.

 

Пример 2.2

Привести ЗЛП к ЗЛП в канонической форме, в которой направление оптимизации - максимизация:

z = 3x₁ – 5x₂ → min,

4x₁ + 7x₂ ≤ 6,

5x₁ + 2x₂ ≥ 8,

3x₁ – 3x₂ ≥ 5,

x₁, x₂ ≥ 0.

Решение

Для изменения направления оптимизации нужно умножить целевую функцию задачи на (–1)). В первое ограничение введём остаточную переменную, а в два последних – избыточные переменные. Каноническая форма задачи выглядит таким образом:

z = –3x₁ + 5x₂ + 0s₁ + 0s₂ + 0s₃ → max,

4x₁ + 7x₂ + s₁ = 6,

5x₁ + 2x₂ – s₂ = 8,

3x₁ – 3x₂ – s₃ = 5,

x₁, x₂, s₁, s₂, s₃ ≥ 0.

 

Пример 2.3

Привести к канонической форме ЗЛП.

max z = 13x₁ – 20x₂,

x₁ + 2x₂ ≤ 6,

-2x₁ + 7x₂ ≥ 8,

x₁, ≥ 0,

x₂ <=> 0.

Решение

В этом случае на переменную x₂ не накладывается ограничение неотрицательности. Введя две новые неотрицательные переменные x₂⁺≥0, x₂^–≥0, исходную переменную x₂ можно исключить путём замены: x₂ = x₂⁺ – x₂^–.

Целевая функция будет иметь вид:

max z = 13x₁ – 20(x₂⁺ – x₂^–).

 

После раскрытия скобок:

max z = 13x₁ – 20x₂⁺ + 20x₂^–.

 

Так как первое ограничение имеет знак “≤”, то в левую часть ограничения вводим остаточную переменную s₁, а вместо переменной x₂ подставляем разность: x₂⁺ – x₂^–. Получим систему:

x₁ + 2x₂⁺ – 2x₂^– + s₁ = 6,

s₁ ≥ 0.

Второе ограничение имеет знак “≥”, значит в левую часть ограничения вводим избыточную переменную s₂, а вместо переменной x₂, как в и предыдущем ограничении, подставляем разность:

-2x₁ + 7x₂⁺ – 7x₂^– – s₂ = 8,

s₂ ≥ 0.

 

Итак, каноническая форма после всех преобразований имеет вид:

max z = 13x₁ – 20x₂⁺ + 20x₂^– + 0s₁ + 0s₂ → max,

x₁ + 2x₂⁺ – 2x₂^– + s₁ = 6,

-2x₁ + 7x₂⁺ – 7x₂^– – s₂ = 8,

x₁, x₂⁺, x₂^–, s₁, s₂, ≥ 0.

Упражнения

1) Укажите, какая из ниже приведенных форм задач является канонической?

а)	б)
в)	г)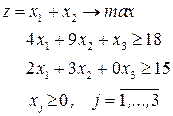
д)	е)

2) Укажите, какая из ниже приведенных задач является стандартной формой задачи линейного программирования(ЗЛП).

а)	б)
в)	г)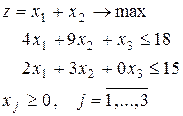

 

3. Основные свойства ЗЛП

Для ЗЛП справедлива следующая теорема.

Теорема (о существовании решения). Если допустимое множество X ЗЛП не пусто, а значение её конечно, то эта задача имеет решение.

 

Определение. Множество, образованное пересечением конечного числа полупространств и гипер­плос­костей, если оно не пусто, называется многогранным множеством.

Определение. Многогранником называется ограниченное многогранное множество.

Множество допустимых решений ЗЛП представляет собой многогранное множество.

Теорема. Пусть допустимое множество X ЗЛП max c^Tx, x X является многогранником. Тогда ЦФ c^Tx достигает своего максимума в вершине X. Если функция c^Tx принимает максимальное значение более чем в одной точке, то она достигает того же значения в любой точке, являющейся их выпуклой линейной комбинацией [5].

 

Из этой теоремы вытекает, что множество оптимальных точек не может быть конечным, если опти­мальная точка не единственна [9].

Алгебраическая запись ЗЛП в канонической форме такова:

Пусть задача (6) имеет допустимые решения и ранг матрицы A равен m (числу ограничений-равенств). Это предположение о ранге практически не является ограничивающим. Этого можно добиться, исключив из системы Ax=b линейно зависимые уравнения.

Кроме того, будем считать, что n>m, т.к. случай n=m не представляет интереса, а соотношение n<m невозможно, так как в этом случае ранг не может быть равен m.

Задачу (6) можно трактовать следующим образом: из всех представлений вектора b в виде линейной комбинации векторов a_*j, j= с неотрицательными коэффициентами выбрать такое (если оно сущест­вует), коэффициенты которого максимизируют значение функции c^Tx. [11]

Система ограничений ЗЛП (6) в векторной форме:

Определение. Базисом ß матрицы A называется набор линейно-независимых столбцов: ß= .

Определение. Базисной матрицей B называется матрица, составленная из столбцов, входящих в базис матрицы A: B .

Матрица B является невырожденной m ×m матрицей.

Определение. Базисным решением, соответствующим ß, называется вектор x Rⁿ, в котором:

– x_j=0 при a_*j ß,

– x_jk есть k-я компонента вектора B^–1b, где k=1,..,m.

Таким образом, базисное решение x можно найти с помощью следующей процедуры:

– выбрать множество линейно независимых столбцов в матрице A;

– положить все компоненты вектора x, соответствующие столбцам, не входящим в базис ß, равными 0. Эти переменные будем называть небазисными;

– решить m полученных уравнений для определения оставшихся m компонент вектора x. Они будут называться базисными переменными.

Определение. Решение x будем называть допустимым базисным решением (ДБР), если оно является базисным и все его компоненты неотрицательны.

Если нулевой вектор является допустимым, то его всегда будем считать базисным.

Определение. ДБР называется невырожденным, если оно имеет точно m положительных компонент (координат). Если число положительных компонент меньше m, то решение называется вырожденным.

Теорема. Вектор x=(x₁, x₂,…, x_n)^T тогда и только тогда является допустимым базисным решением задачи (6), когда точка x=(x₁, x₂,…, x_n)^T является вершиной его многогранного множества X.

Теорема (фундаментальная). Если ЗЛП имеет оптимальное решение (в ограниченной области всегда, а в неограниченной – в зависимости от ограниченности целевой функции ), то оно совпадает, по крайней мере, с одним из ДБР системы ограничений.

 

4. Идея симплекс – метода

Согласно фундаментальной теореме вместо исследования бесконечного множества допустимых решений, необходимо исследовать лишь конечное число ДБР. Таким образом, принципиальная схема решения ЗЛП такова[7]:

– найти все ДБР;

– вычислить для каждого из них соответствующее значение ЦФ z;

– сравнить и определить наилучшее.

Но, в общем случае при больших значениях n и m количество ДБР может быть огромным (порядка C_n^m) и практическое осуществление перебора всех ДБР станет невозможным. Эти трудности обусловлены тем, что указанная принципиальная схема связана с беспорядочным пе­ре­бором ДБР, без учета, насколько новое проверяемое ДБР изменяет ЦФ z и приближает ли оно нас к иско­мому оптимуму. Если же указанный перебор ДБР производить целеустремленно, добиваясь на каждом шаге монотонного изменения ЦФ z, т.е. чтобы каждое следующее ДБР было лучше предыдущего (или, по крайней мере, не хуже), то число анализируемых ДБР можно резко сократить.

Основной метод решения ЗЛП – симплекс-метод – базируется на идее последовательного улучше­ния решения. Очевидно, что для реализации этой идеи метод должен включать три основных элемента:

– способ определения исходного ДБР;

– правило перехода к следующему “лучшему” ДБР;

– критерий, по которому можно определить оптимальность найденного решения или необходи­мость его дальнейшего улучшения.

 

5. Преобразованная задача

Рассмотрим ЗЛП в канонической форме:

Пусть нам известно некоторые ДБР x системы ограничений (8). Не теряя общности, предположим, что первые m столбцов матрицы A образуют базис данного ДБР.

Обозначим через B базисную матрицу для ДБР x (первые m столбцов матрицы A), а через N – матрицу, составленную из остальных столбцов матрицы A. Тогда

В соответствии с представлением (10) разобьем вектор x на подвекторы x_B и x_N, т.е.

где x_B – вектор базисных переменных, а x_N – вектор небазисных переменных.

Систему (8) можно записать в виде:

Так как матрица B – невырожденная, то она имеет обратную матрицу B^–1 тогда

Система (12) эквивалентна системе (11).

Теперь разобьем вектор c на подвекторы c_B и c_N, в соответствии с разбиением (10) матрицы A.

Тогда задачу (7)–(9) можно записать в виде:

Подставим значение x_B в ЦФ задачи:

Тогда исходная задача может быть представлена в виде:

Получили так называемую преобразованную задачу. Обозначив

можно записать преобразованную задачу следующим образом:

Так как x_N=0, то x_B принимает числовое значение β, а ЦФ – значение c_B^Tβ. Однако, в преобразованную задачу включаются все члены правых частей уравнений (не смотря на то, что x_N=0), т.к. они указывают на то, что произойдет с ЦФ и x_B, если один из элементов вектора x_N увеличивается, начиная с нуля.

Иногда задачу (13)-(15) называют диагональной формой исходной задачи, соответствующей ДБР x, а система (14) называется диагональной системой относительно переменных x₁,x₂,…,x_m. Система названа диагональной, потому что представима в виде:

Очевидно, что наше ДБР .

 

6. Способ перехода от одного ДБР к другому

Пусть ДБР x⁰ соответствует преобразованной задаче (13)-(15). Перейдем от него к новому ДБР x¹. При этом рассмотрим возможность того, что только одна небазисная переменная станет возрастать, принимая по­ложительные значения, в то время как остальные небазисные переменные останутся нулевыми [10]. Обозначим

и запишем систему ограничений преобразованной задачи по столбцам:

.

Пусть начиная с нуля, возрастает переменная (xN) p, значит, вектор базисных переменных изменяется согласно уравнению

так как другие небазисные переменные остаются равными нулю. При этом, в зависимости от значений ком­понент вектора a
*p возможны 3 следующих случая:

– если ая компонента вектора равна нулю (), то соответствующий ей элемент вектора останется без изменений;

– если ая компонента вектора отрицательна (), то соответствующий ей элемент будет увеличиваться;

– если ая компонента вектора положительна () – соответствующий ей элемент будет уменьшаться и станет меньше нуля, когда величина (x_N)_p сделается достаточно большой. Этого допустить нельзя, т.к. будет нарушена допустимость x¹.

 

Отсюда получаем максимально допустимое увеличение значения (x_N)_p

где a_ip и β_i – элементы векторов a_*p и β соответственно.

Пусть минимум в этом уравнении достигается при i=q тогда, если , то в новом ДБР имеем:

Отметим, что выбор q однозначен. Если уже выбрана увеличиваемая небазисная переменная p-я, то базисная q-я, которая первая обратится в нуль, определяется величинами a _*p и β. Если в нуль обращаются одновременно две или более базисных переменных, мы имеем дело с вырожденным случаем, однако выбрать мы должны только одну из них.

Итак, мы пришли к следующей ситуации: переменная (x_N)_p стала базисной со значением , а переменная (x_B)_q – небазисной (со значением 0). Это означает такую перестановку в разбиении матрицы A, что столбец a_*p становится на место q-го столбца матрицы B. В этом случае будем говорить, что (x_N)_p «вводится» в базис, а (x_N)_p «выводится» из него.

Описанный способ перехода от одного ДБР к другому называется операцией замещения.

 

7. Условие оптимальности ДБР

Определение.Вектор-строка, на которую умножается слева x_N в уравнении для ЦФ (13), называется век­тором относительных оценок, т.к. он указывает, в какую сторону и насколько изменится ЦФ при изменении x_N.

Обозначим этот вектор через d_N. Его j-ый элемент определяется так:

Если относительная оценка (d_N)_j, то небазисной переменной (x_N)_j положительна или равна нулю, но значение ЦФ не увеличивается при увеличении (x_N)_j, начиная с нуля [11].

Теорема (условие оптимальности).Для ДБР x⁰ операция замещения, при которой (x_N)_p вводится в базис, изменяет значение ЦФ на величину

где

Если d_N≥0, то x⁰ оптимально.

ЗЛП будем называть невырожденной, если все ее ДБР не вырождены. Справедлива теорема, обратная последней теореме.

Теорема. Пусть ЗЛП является невырожденной, а x⁰ – ДБР, являющееся ее решением. Тогда d_N≥0.

В том случае, если ЗЛП не является невырожденной, предыдущая теорема приобретает вид:

Теорема. Для того, чтобы ДБР x⁰ являлось решением исходной ЗЛП, необходимо и достаточно су­ществование такого базиса для x⁰, для которого d_N≥0.

Теорема. Если некоторому ДБР исходной задачи соответствует задача, для которой существует не­базисная переменная (x_N)_p такая, что (d_N)_p<0 и (a_N)_*p≤0, то целевая функция исходной задачи не ограни­чена на множестве допустимых решений (θ не ограничено сверху и можно сколько угодно увеличивать целевую функцию).

 

Пример 7.1

Дана ЗЛП

.

Знайти всі компоненти перетвореної задачі для ДБР, який відповідає базису . Чи є оптимальним цей ДБР?

Розв’язок

Базисні, небазисні змінні та відповідні їм векторикоєфіцієнтів ЦФ:

.

Небазисна матриця та вектор правих частин обмежень:

.

Базисна матриця та матриця, обернена до неї:

.

Значення базисних змінних та ЦФ:

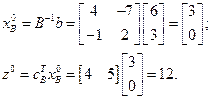
Вектор відносних оцінок небазисних змінних:

Оскільки вектор відносних оцінок небазисних змінних містить додатні компоненти, а задача на максимум, то поточний базисний розв'язок не є оптимальним.

 

8. Схема симплекс-метода

Рассмотренные в разделах 6-7 способы перехода от одного ДБР к другому и теоремы ЛП, позволяют построить так называемый симплекс-метод решения ЗЛП в канонической форме, который имеет сле­дующую схему:

 

Шаг 0. Построение начального ЗЛП.

Пусть задано ДБР x⁰ исходной ЗЛП (такое ДБР называется начальным). Пусть данному ДБР соот­ветствует базис ß, вектор базисных переменных x_B=B^–1β, небазисных переменных x_N, базисная матрица B, небазисная матрица N.

Шаг 1. Вычисление компонент вектора относительных оценок небазисных переменных.

Шаг 2. Проверка выполнения условия оптимальности.

Если выполняется d_N≥0, то прекратить вычисления – текущее ДБР является решением исходной задачи. Иначе – перейти на шаг 3.

Шаг 3. Выбор небазисной переменной (x_N)_p, вводимой во множество базисных переменных.

Выбрать p, для которого (d_N)_p<0 (обычно p соответствует максимальная по модулю отрицательная компонента d_N).

Шаг 4. Выбор базисной переменной, выводимой из множества базисных переменных.

Вычислить a_*p=B^–1 a_*p (пересчет столбца вводимого в базис).

Если a_*p<0, то прекратить вычисления – целевая функция не ограничена сверху.

Выбрать q, для которого выполняется , т.е. переменная (x_B)_q будет выведена из множества базисных переменных.

Шаг 5. Операция замещения.

Построить базис нового ДБР путем замены q-го столбца a_*p текущего базиса ß на столбец a_*p. Построить новые базисную матрицу B и небазисную матрицу N. Найти новые значения базисных переменных x_B=B^–1b и ЦФ c_B^Tβ.

Перейти на шаг1.

 

 

Пример 4

Дана система ограничений:

Являются ли базисами данной системы, следующие множества векторов,

– ,

– ,

– .?

если да, то какие решения им соответствуют:

Решение. Базисом β матрицы А называется набор из линейно-независимых столбцов β= .

Решение называется допустимым базисным решением если оно является базисным и все его компоненты не отрицательны.

В нашей задаче m= 3, n= 5. То есть количество претендентов на базис в нашей задаче будет не более, чем .

а) Рассмотрим первое множество векторов - . Составим матрицу из этих векторов, если её детерминант будет отличен от нуля, то эти векторы составляют базис:

.

Значит, совокупность векторов является базисом исходной системы уравнений. Выпишем уравнения системы с учетом того, что небазисные переменные принимают нулевые значения:

Соответствующее базисное решение имеет вид:

- небазисные переменные переменные

b) Рассмотрим множество векторов - .

Теперь составим матрицу из соответствующих векторов и найдём её определителю:

Значит множество векторов является базисом. Найдём соответствующее ему базисное решение, для этого выпишем уравнения системы с учетом того, что :

Итак, данному базису соответствует решение:

базисные переменные

небазисная переменная

базисная переменная

небазисная

По условию нашей задачи , а в решении только две базисные переменные положительны, следовательно, имеем вырожденное ДБР (так как у него количество положительных координат меньше ).

с) Рассмотрим множество векторов - .

Составим матрицу из этих векторов,

Значит множество векторов является базисом.

Выпишем уравнения системы с учетом того, что :

Таким образом, соответствующее базисное решение таково:

- небазисые переменные

- базисные переменные

- базисная переменная

Итак, базису соответствует решение, у которого одна переменная отрицательна, следовательно, имеем недопустимое базисное решение.

 

9. Табличный симплекс-метод

Пусть для исходной ЗЛП задано начальное ДБР, базис которого образуют первые m столбцов матри­цы A. Введем новую переменную z и с помощью элементарных преобразований Жордана-Гаусса преобразуем расширенную систему к диагональной форме относительно переменных z, x₁, x₂,…, x_m:

,

,

Диагональная форма (19) исходной системы ограничений, полученная при помощи преобразований Жордана-Гаусса, совпадает с диагональной формой (13)-(15), полученной матричным способом.

Диагональной форме (19) можно поставить в соответствие следующую таблицу, которая получила название симплекс-таблицы:

Таблица 1

БП	z	x1	…	xm	xm+1	…	xn	Решение
z			…			…		b0
x1			…		a1,m+1	…	a1,n	b1
…	…	…	…	…	…	…	…	…
xm			…		am,m+1	…	am,n	bm

 

В левом столбце таблицы перечислены базисные переменные. В общем случае в этом столбце таблицы в i-ой строке будет записана переменная (x_B)_i.

Слева от таблицы указаны базисные переменные.

В общем случае в левом столбце таблицы в i-ой строке будет записана переменная .

 

Построенная таблица называется симплекс-таблицей. Она содержит всю информацию, необходимую для осуществления одной итерации симплекс-метода. Реализация симплекс-метода с помощью симплекс-таблицы называется табличным симплекс-методом.

По сути, симплекс-метод и табличный симплекс-метод соотносятся между собой как метод и алгоритм.

В дальнейшем столбец будем опускать, так как от итерации к итерации он не изменяется.

 

9.1. Схема табличного симплекс-метода

Шаг 0. Начальный шаг

Построить начальное ДБР исходной задачи.

Построить соответствующую этому ДБР симплекс-таблицу.

 

Шaг 1. Проверка условия оптимальности

ЕСЛИ коэффициенты z -строки

неотрицательны - в случае задачи на максимум

(неположительны - в случае задачи на минимум),

ТО прекратить вычисления: текущей симплекс-таблице соответствует оптимальное ДБР.

 

Шаг 2. Выбор переменной, вводимой в базис.

Среди коэффициентов выбрать отрицательный.

Пусть мы выбрали .

Переменная будет вводиться во множество базисных переменных, а -й столбец будет ведущим.

 

Шаг 3. Выбор переменной, выводимой из базиса

ЕСЛИ все коэффициенты ведущего столбца неположительные, то прекратить вычисления: целевая функция не ограничена сверху.

ИНАЧЕ выбрать переменную , которой соответствует минимум в выражении

.

-ая строка называется ведущей.

Элемент таблицы на пересечении ведущих строки и столбца называется ведущим элементом.

Шаг 4. Переход к новому ДБР <