Внешнюю нагрузку, приложенную к кольцу, представим в виде ряда:
 . (2.14)
. (2.14)
Коэффициенты ряда (2.14) определяются при интегрировании левой и правой его частей в пределах от 0 до 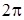 :
:
Таблица 2.1 – Безразмерные силовые факторы и перемещения для кольца
| φ, ° | Q | M | N | v | w |
| 0.00 | 0.0000 | 0.1271 | -0.3579 | 0.0000 | -0.0346 |
| 10.00 | -0.1118 | 0.1173 | -0.3628 | 0.0059 | -0.0322 |
| 20.00 | -0.2218 | 0.0882 | -0.3776 | 0.0110 | -0.0253 |
| 30.00 | -0.3285 | 0.0401 | -0.4022 | 0.0145 | -0.0149 |
| 40.00 | -0.2563 | -0.0110 | -0.4215 | 0.0161 | -0.0029 |
| 50.00 | -0.1825 | -0.0493 | -0.4206 | 0.0156 | 0.0088 |
| 60.00 | -0.1106 | -0.0748 | -0.4006 | 0.0131 | 0.0189 |
| 70.00 | -0.0437 | -0.0882 | -0.3637 | 0.0091 | 0.0261 |
| 80.00 | 0.0155 | -0.0905 | -0.3124 | 0.0042 | 0.0299 |
| 90.00 | 0.0648 | -0.0833 | -0.2500 | -0.0011 | 0.0300 |
| 100.00 | 0.1024 | -0.0686 | -0.1800 | -0.0061 | 0.0268 |
| 110.00 | 0.1274 | -0.0483 | -0.1061 | -0.0103 | 0.0206 |
| 120.00 | 0.1394 | -0.0249 | -0.0324 | -0.0132 | 0.0124 |
| 130.00 | 0.1389 | -0.0004 | 0.0375 | -0.0145 | 0.0030 |
| 140.00 | 0.1267 | 0.0229 | 0.1001 | -0.0142 | -0.0065 |
| 150.00 | 0.1045 | 0.0433 | 0.1522 | -0.0123 | -0.0151 |
| 160.00 | 0.0744 | 0.0590 | 0.1914 | -0.0090 | -0.0219 |
| 170.00 | 0.0386 | 0.0689 | 0.2157 | -0.0048 | -0.0263 |
| 180.00 | 0.0000 | 0.0723 | 0.2239 | 0.0000 | -0.0278 |
| 190.00 | -0.0386 | 0.0689 | 0.2157 | 0.0048 | -0.0263 |
| 200.00 | -0.0744 | 0.0590 | 0.1914 | 0.0090 | -0.0219 |
| 210.00 | -0.1045 | 0.0433 | 0.1522 | 0.0123 | -0.0151 |
| 220.00 | -0.1267 | 0.0229 | 0.1001 | 0.0142 | -0.0065 |
| 230.00 | -0.1389 | -0.0004 | 0.0375 | 0.0145 | 0.0030 |
| 240.00 | -0.1394 | -0.0249 | -0.0324 | 0.0132 | 0.0124 |
| 250.00 | -0.1274 | -0.0483 | -0.1061 | 0.0103 | 0.0206 |
| 260.00 | -0.1024 | -0.0686 | -0.1800 | 0.0061 | 0.0268 |
| 270.00 | -0.0648 | -0.0833 | -0.2500 | 0.0011 | 0.0300 |
| 280.00 | -0.0155 | -0.0905 | -0.3124 | -0.0042 | 0.0299 |
| 290.00 | 0.0437 | -0.0882 | -0.3637 | -0.0091 | 0.0261 |
| 300.00 | 0.1106 | -0.0748 | -0.4006 | -0.0131 | 0.0189 |
| 310.00 | 0.1825 | -0.0493 | -0.4206 | -0.0156 | 0.0088 |
| 320.00 | 0.2563 | -0.0110 | -0.4215 | -0.0161 | -0.0029 |
| 330.00 | 0.3285 | 0.0401 | -0.4022 | -0.0145 | -0.0149 |
| 340.00 | 0.2218 | 0.0882 | -0.3776 | -0.0110 | -0.0253 |
| 350.00 | 0.1118 | 0.1173 | -0.3628 | -0.0059 | -0.0322 |
| 360.00 | 0.0000 | 0.1271 | -0.3579 | 0.0000 | -0.0346 |
 ;
;
 ;
; 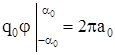 ;
;
 ;
; 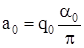 .
.
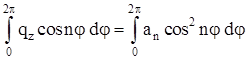 ;
;
 ;
;
 ;
;
 ;
;
 .
.
В результате ряд для 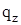 принимает вид:
принимает вид:
 . (2.15)
. (2.15)
Дифференциальное уравнение для перемещения v имеет вид [1, с. 108]:
 . (2.16)
. (2.16)
Перед слагаемым  стоит знак «–», так как погонные нормальные силы
стоит знак «–», так как погонные нормальные силы 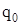 , направлены в сторону, противоположную принятому при выводе этого уравнения положительному направлению для
, направлены в сторону, противоположную принятому при выводе этого уравнения положительному направлению для 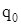 .
.
Подставляя в уравнение (2.16)
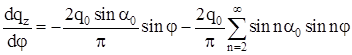 ,
,
 ,
,
получим:
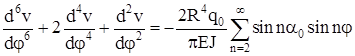 . (2.17)
. (2.17)
Подставив в это уравнение выражение для перемещения v в виде ряда

и приравняв коэффициенты при соответствующих функциях в уравнении
 ,
,
получим:
 ;
;
 . (2.18)
. (2.18)
Из условия нерастяжимости кольца
 ;
;
 . (2.19)
. (2.19)
Представим эти перемещения в безразмерном виде
 и
и 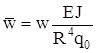 .
.
Окончательно
 (2.20)
(2.20)
Эпюры безразмерных перемещений и форму деформированного кольца построим с помощью пакета MathCAD (приложение 4). Результаты приведены в таблице 2.1 и представлены на рисунках 2.2 и 2.3.
Определение размеров поперечного сечения шпангоута
Выберем [3, с. 304] поперечное сечение шпангоута в виде двутаврового профиля (рисунок 2.4). Определим размеры этого сечения, если кольцо изготовлено из сплава В95 [2, с. 43], для которого с учетом коэффициента запаса

Рисунок 2.3 – Форма деформированного кольца

Рисунок 2.4 – Геометрические параметры сечения шпангоута
по пределу текучести ( ) допускаемые напряжения
) допускаемые напряжения  . Расчет проведем для сечения шпангоута при
. Расчет проведем для сечения шпангоута при  (приложение 5). Здесь
(приложение 5). Здесь
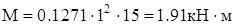 ;
;
 ;
;
 .
.
Задаемся [3, с. 306]:
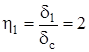 ;
;  ;
;
 ;
;  .
.
Площадь сечения шпангоута
 ;
;
 ,
,
расстояние до нейтральной оси
 ;
;
 ,
,
собственный момент инерции сечения
 ;
;
 .
.
Напряжения в наружной полке
 , (2.21)
, (2.21)
во внутренней полке
 . (2.22)
. (2.22)
M и N подставляются в формулы (2.21) и (2.22) с теми знаками, которые получаются при их вычислении.
Назначим толщину стенки  и найдем
и найдем  .
.
Теперь толщина и ширина полок:
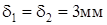 ;
;  ;
; 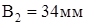 .
.
Сечение шпангоута в масштабе 1:1 изображено на рисунке 2.5.
Нормальные напряжения в полках:
 ;
;  .
.
Определим максимальные касательные напряжения в стенке шпангоута для сечения при  (
( ):
):
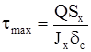 . (2.23)
. (2.23)
Статический момент части площади сечения, расположенной выше нейтральной оси, относительно этой оси
 ;
;
 .
.
После расчета получим
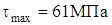 .
.

Рисунок 2.5 – Сечение шпангоута в масштабе 1:1