Шкала интервалов - позволяет находить разницу между двумя величинами. Позволяет указать количественное значение измеряемого признака. Состоит из интервалов одинаковой длины, называемых единицей измерения. Обладает всеми свойствами порядковой и номинальной шкал. Недостаток шкалы - отсутствие абсолютного нуля как точки отсчета. Интервальные шкалы делимы теоретически до бесконечности и являются непрерывными в отличии от номинальной и порядковой шкал, которые являются дискретными. Дискретные числовые данные - это отдельные значения признаков, общее число которых конечно или если оно бесконечно, то является счетным. Непрерывные числовые данные могут принимать любые значения в заданном интервале. Непрерывные шкалы позволяют проводить точные измерения значений признака, с которыми можно проводить арифметические операции.
Шкала отношений - обладает абсолютным нулем в качестве точки отсчета, что позволяет ей иметь все свойства интервальной шкалы. Для данных этой шкалы применимы все арифметические операции.
Признак - это некоторая общая для всех изучаемых объектов характеристика или свойство, конкретное проявление которого могут меняться от объекта к объекту.
Проявления признака называют значениями, альтернативами, градациями.
Признаки делятся на:
- качественные и количественные
- Основные (существенные) и второстепенные
- Первичные и вторичные
Под качественными признаками понимают такие признаки, определенные значения которых отличаются друг от друга атрибутивными свойствами или существенными моментами.
Количественные признаки - это те, отдельное значение которых отличается друг от друга по величине. Выражается числом.
Основные признаки определяют главное содержание процесса.
Второстепенные дают добавочные сведения о свойствах и несвязанных непосредственно с внутренним содержанием явлений.
Первичные получают при сборе статистических данных, а вторичные при обработке этих данных.
При статистическом исследовании рассматривается распределение переменной, то есть совокупность различных значений, которые переменная принимает для различных изучаемых объектов.
Социологи чаще всего не имеют возможности рассматривать всю интересующую их совокупность. Вполне достаточно изучить некую выборку, чтобы получить информацию о всей совокупности.
Генеральная совокупность - эта вся интересующая исследователя совокупность изучаемых объектов. Выборка (выборочная совокупность) - часть генеральной совокупности, отбираемая специальным образом и исследуемая с целью получения выводов о свойствах генеральной совокупности.
Показатель - обобщающая количественная характеристика явлений (процессов) в их качественной определенности в условиях конкретного места и времени.
Систему показателей образует несколько показателей, всесторонне отражающих развитие явления.
Вариация - колеблемость, многообразие, изменяемость величин признака у отдельных единиц совокупности.
Пределы, в которых возможны изменения величины количественного признака, называются границами вариаций.
Лекция 2. Основы применения методов прикладной статистики в социологических исследованиях. Группировки социологических исследований.
Процесс научного познания складывается из трех компонентов:
1) методология - это совокупность основополагающих представлений, идей, принципов познания, которые являются теорией метода.
2) Методика исследования - пути и способы их реализации, набор соответствующих правил и процедур
3) Техника - конкретный инструмент исследования
Все компоненты взаимосвязаны и не могут существовать в отрыве друг от друга.
В основе современных математико-статистических теорий лежит понятие вероятность, то есть мера возможности того или иного результата, характеризующая с количественной определенностью возможность появления данного события. Вероятность = отношение число возможных случаев, благоприятствующих данному событию к числу всех равнозначных случаев. Для вероятностных событий необходимо выполнение ряда условий:
1) наблюдаемые явления либо могут повторены неограниченное число раз, либо сразу осуществляется наблюдение за одинаковыми явлениями в большом количестве.
2) Независимость событий
3) Наличие постоянных условий при создании базы данных
Закономерности бывают динамическими, которые проявляются в единичном случае и статистическими, которые проявляются в группе явлений. Характер динамической закономерности устанавливает поведение каждого признака, а статистическое наряду с признаками, присущими индивидуальным явлениям характеризуют общие для всех признаки. Общественные явления складываются из масс индивидуальных и найти закономерность значит найти повторяемость внутри всей массы явлений, где наряду с главными действует множество второстепенных, неустойчивых, случайных факторов.
Следовательно, в обществе нет строго определенных динамических закономерностей.
Статистические закономерности теоретически базируются на законе больших чисел - только при большом количестве наблюдений формируются и проявляются многие объективные закономерности общественных явлений. Влияние случайных факторов второстепенно тем меньше, чем больше рассмотрено единичных явлений.
В научной литературе нет единого понимания роли статистических закономерностей в социологии. Чаще всего, говоря о статистичности социальных закономерностей, имеется в виду законы развития больших социальных групп и общество в целом. Но статистические модели вполне могут использоваться при попытке понять отдельного человека. Например, применение статистического подхода к изучению представлений одного человека - использование статистических распределений для описания неоднозначности мнения одного респондента относительного одного объекта. Такой подход используется во многих методах шкалирования. Например, терстоунская модель метода парных сравнений или модель подражательного поведения Рашевского. Статистическая модель не всегда имеет смысл.
В процессе исследования соотношение количественного и качественного анализа проходит 4 этапа:
1) постановка проблемы, подготовка и проведение эмпирического исследования, определение интересующих нас признаков, которые мы считаем существенными (преобладает качественный анализ)
2) Выбор математических методов (и качественный, и количественный)
3) Количественный анализ - расчет показателей по формуле
4) Интерпретация полученных результатов, построение на их основе теоретических выводов
Каждый предыдущий этап влияет на последующий и наоборот. Изменение количественных параметров может происходить в рамках одного качества, а может приводить к приобретению явлением нового качества.
Метод группировки заключается в разбиении исходной совокупности данных на группы, каждая из которых объединена общими показателями. Группировка является основным начальным этапом обработки данных и основой для большинства приемов статистического анализа.
Сгрупированные данные чаще всего предоставляются в виде таблиц или графиков. Построение таблицы - это первый этап статистического изучения вариации признаков.
Правила составления таблицы:
1) каждая таблица должна иметь заголовок, отражающий ее внутреннюю структуру.
2) В одной таблице не должно быть много признаков, чтобы не ухудшать наглядность и не осложнять анализ.
3) Итого - это итог для определенной части совокупности, а всего - итог для совокупности в целом.
4) Громоздкие числа нужно округлять.
5) Каждая клетка таблицы должна соответствовать определенному числу. Если сведений нет, то ставится прочерк или многоточие. Если сведения выражены крайне малой величиной, то в таблицу вносится значение 0,0. Если значение получено в результате приближенных вычислений, оно заключается в круглые скобки.
6) Таблицы сопровождаются сносками и примечаниями. Сноски относятся к части таблицы и указывают на ограниченные обстоятельства, которые нужно иметь в виду при чтении отмеченных фрагментов. Примечания относятся ко всей таблице в целом, чаще всего в нем указывается источник информации. Если таблица авторская, в примечании пишете "составлено по данным...". Если таблица взята в готовом виде, указывать источники информации.
Для того, чтобы не потерять информацию и в то же время составить компактную таблицу, используются интервальные ряды. Здесь возникает проблема определения границ интервалов. Необходимо найти оптимальное число групп, количество интервалов признака и установить их размер. Решение этих вопросов зависит от степени однородности совокупности. Если совокупность однородна, берутся равные интервалы. При описании тенденций их лучше укрупнить, а когда значение имеет конкретные данные относительно каждой группы, их лучше уменьшить. Величина интервала - это его разность между верхней и нижней границей. Существует несколько формальных способов определения оптимальной величины интервала, то есть такого его значения, при котором рассматривается специфика явления и в то же время группировка не выглядит громоздкой.
Формула Стерджеса: k = x max - x min / 1 + 3,2 lg n, где к - величина интервала, х мах - наибольшее значение признака, n - число элементов совокупности, х мин - наименьшее значение признака.
Пример: дано 100 рабочих со стажем от одного до 42 лет. Нужно определить оптимальную величину интервала для группировки рассматриваемой совокупности по стажу.
42-1/1+3,2 lg 100 = 5,5
Таким образом, оптимальная величина интервала 5,5.
Границы интервалов для дискретных признаков устанавливаются без совпадений крайних показателей смежных интервалов, чтобы ни одно значение признака не попало в промежуток между интервалами и не было потеряно. Например, группировка учащихся группы. Это объясняется свойствами самого признака, принимающего только целые значения. Для непрерывных признаков или дробных обязательно совпадение смежных границ интервалов. Согласно правилу о совпадении границ интервалов распределение предполагает наличие предлогов от и до. Статистика различает открытые и закрытые интервалы. В первом случае определяется только верхняя или нижняя граница. Во втором случае указывается верхняя и нижняя граница.
В случае неоднородной совокупности в основу строения группировки кладется качественный критерий, призванный выявить однородные типы. Границы интервалов определяются там, где количественное изменение признака приводит к появлению нового качества. В случае необходимости совокупность разбивается на однородные группы, внутри каждой строится своя шкала интервалов. Например, городское население, в основу группировки мы кладем признак принадлежности к различным социальным группам, в случае необходимости каждую эту группу распределяют по какому-то качественному или количественному признаку.
Метод группировки позволяет сложные явления представить через ряд более простых. Им характеризуются типы явлений во взаимных отношениях или взаимосвязях и раскрывается причинная зависимость между отдельными факторами и общими закономерностями.
Различают три основных вида группировок: типологические, структурные и аналитические.
Типологические делят качественно разнородную совокупность на однородные группы. В основе таких группировок лежит качественный признак.
Структурные группировки представляют качественно однородную совокупность в виде количественных групп. В основе лежит количественный признак.
Аналитические позволяют установить и на определенном уровне изучить взаимосвязь между признаками. Такие группировки называют факторными. При этом один из группировочных признаков рассматривается как результат, а другой как фактор. Изучение данных такой группировки должно начинаться с выяснения возможности существования связи между этими признаками. 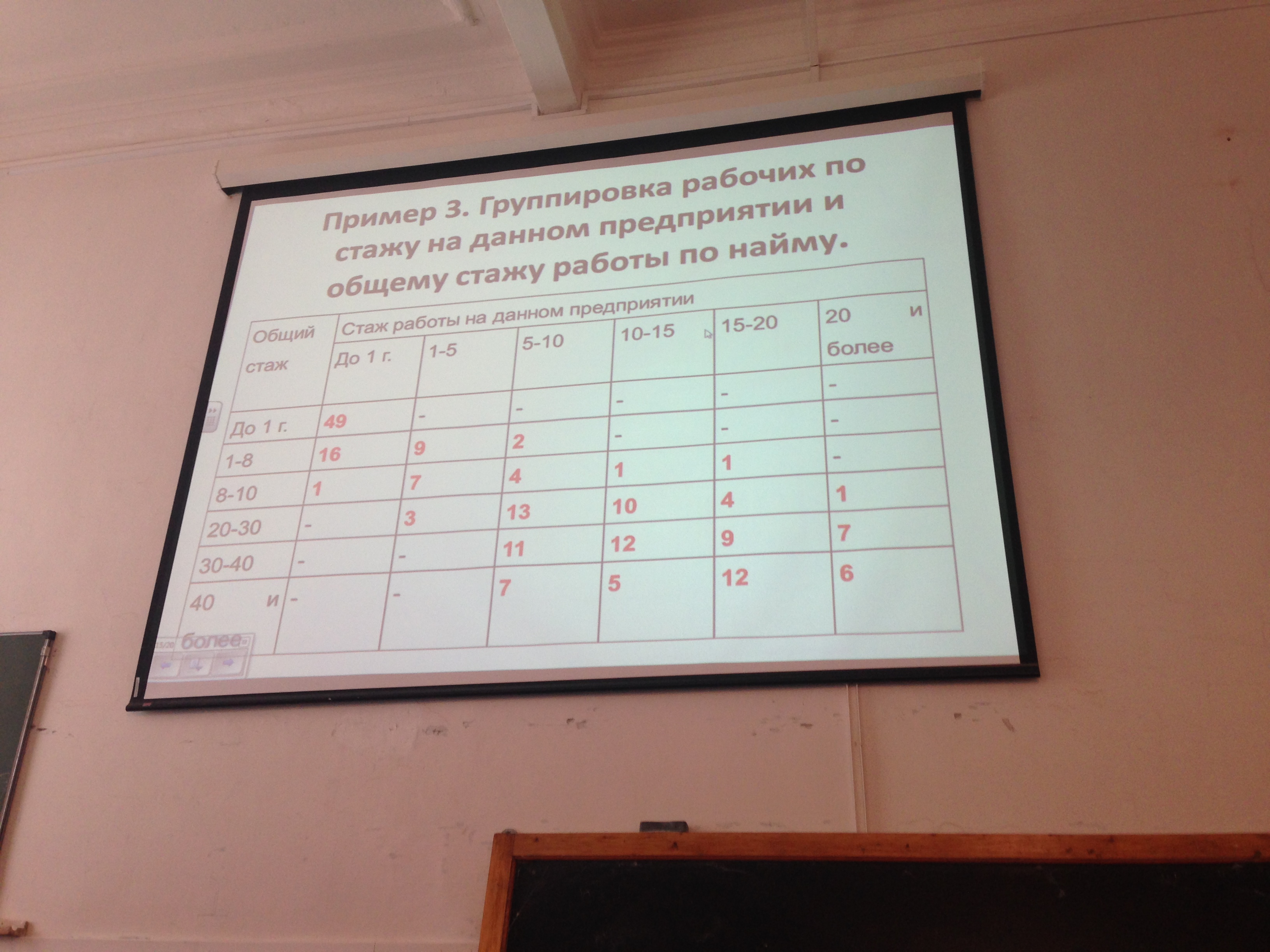
Когда данные в таблице концентрируются по диагонали, это говорит о наличии существенной тесной связи между признаками, а направление диагонали говорит о характере выявленной связи. Если диагональ идет сверху вниз, то связь между признаки прямая. Если снизу вверх - обратная. Прямая связь означает, что увеличение значений одного факторного признака, приведет к увеличению значений второго признака результативного. При обратной связи росту значения факторного признака соответствует уменьшение значений результативного.
Метод группировки позволяет примерно определить роль того или иного признака в изучаемом явлении в силу его влияния на другие характеристики. Для этого используют безусловное распределение (структурная группировка). Если в структурной группировке данные концентрируются в одной группе, то этим признаком можно пренебречь при дальнейшем изучении явлений на уровне взаимосвязи, так как он не будет оказывать заметного влияния на другие. Если показатели безусловного распределения равномерно охватывают изучаемую совокупность объектов, скорее всего этот признак оказывает активное влияние на изучаемые явления. С помощью безусловного распределения можно выявить группу факторов, определяющих изучаемые явления и выделить признаки, имеющие место, но не играющие значительной роли.
Одним из важных моментов использования данного метода является выбор группировочного признака. От приема группировки и базового признака во многом зависят выводы, которые можно получить на основе одних и тех же материалов изучаемых одним и тем же методом группировки. Главное требование группировочного признака - достоверность отражения структуры изучаемого явления в зависимости от времени и конкретных условий.
Особое место среди группировок занимают динамические ряды. Они бывают моментные (в которых время задано в виде конкретных дат) и интервальные (где время задано в виде промежутков).
Показатели временного ряда (уровни, элементы) Xt, где t - время.
Изучение динамических рядов начинается с доказательства требований, использовавшихся при их построений:
1) Однородность явлений относительно каждой динамической группы, то есть в один временной промежуток должны включаться одни и те же явления.
2) Неизменность территории, к которой относятся показатели.
3) Единство методологии учета показателей. Уровни динамического ряда могут задаваться абсолютными, относительными или средними величинами. Соответственно и уровни динамического ряда.
4) Временной показатель, положенный в основу динамического ряда, в случае его интервальной разбивки должен иметь сопоставимые временные промежутки.
Показатели динамического ряда считаются сравнимы ми при выполнении всех четырех условий.