Изучение нового материала
В большинстве случаев тело взаимодействует не с одним телом, а с несколькими телами одновреме́нно. К примеру, на машину действует сила тяжести со стороны Земли, сила реакции опоры со стороны дороги на колёса, силы сопротивления движению и, конечно же, сила тяги двигателя. Поэтому в механике важную роль играют понятия результирующая сила и равнодействующая сила.
Результирующая двух или нескольких сил — это сила, равная их векторной сумме.
А равнодействующей двух или нескольких сил называется сила, которая оказывает такое же действие, как эти силы совместно. Иначе говоря, равнодействующая может полностью заменить исходные силы.
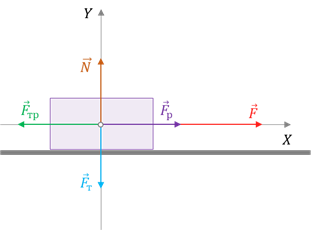
Если посмотреть на эти два определения, то кажется, что они довольно-таки похожи. То есть результирующая и равнодействующая силы — это одна и та же сила. Но так ли это? Пусть у нас с вами есть брусок, к концам которого приложены две одинаковые по модулю, но разные по направлению силы. Очевидно, что под действием этих двух сил брусок начнёт вращаться.

Но ведь их результирующая равна нулю. А сила, которая равна нулю, не может вызвать вращение тела. Следовательно, в этом примере результирующая сила не является равнодействующей, так как она не заменяет действия данных сил. Это надо учитывать при решении задач, несмотря на то, что мы с вами чаще всего будем рассматривать задачи, в которых тело можно принять за материальную точку. В этом случае допускается считать, что силы приложены к телу в одной точке.
Мы уже с вами знаем, что в результате действия силы тела приобретают ускорение. Поэтому логично предположить, что между этими величинами должна существовать какая-то количественная взаимосвязь. Установим её. Для этого рассмотрим поступательное движение металлического бруска, так как только при поступательном движении ускорение всех точек тела одинаково и мы можем говорить об ускорении тела в целом. Чтобы свести к минимуму действие силы трения, положим брусок на тележку с лёгкими колёсами. Пусть на тележку со стороны нити, к концу которой прикреплён груз, действует внешняя сила, модуль которой мы можем измерять при помощи динамометра.
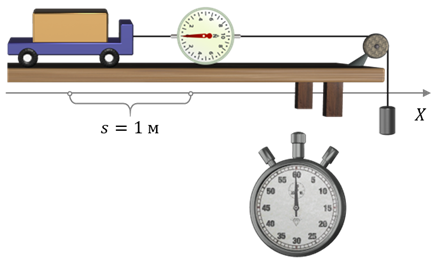
Если отпустить груз, то тележка придёт в движение. Если предположить, что ускорение во время движения было постоянным, то, измерив время движения тележки и путь, пройденный ею за это время, мы по формулам кинематики сможем легко определить её ускорение.
Повторим опыт ещё пару раз, увеличив внешнюю силу в два и три раза путём увеличения массы груза, подвешенного на нити.

Не трудно заметить, что увеличение модуля внешней силы в несколько раз приводит к увеличению модуля ускорения тележки во столько же раз. Значит, отношение модуля силы к модулю ускорения тела является постоянной величиной, не зависящей от силы. Эту величину мы с вами будем называть массой тела.
На прошлом уроке мы с вами говорили о том, что масса является количественной мерой инертности тел. То есть, чем больше масса тела, тем оно более инертно и тем медленнее меняется его скорость под действием постоянной силы. Следовательно, модули ускорений, приобретаемых телами под действием одинаковых сил, обратно пропорциональны массам этих тел.
Полученные нами закономерности можно выразить одной формулой:
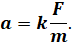
Мы уже вспоминали о том, что единицей силы в СИ является ньютон. Один ньютон — эта сила, которая сообщает телу массой 1 кг ускорение 1 м/с2.
Поэтому в СИ коэффициент k = 1.
Таким образом, ускорение, приобретаемое телом под действием приложенных к нему сил, прямо пропорционально равнодействующей силе, обратно пропорционально массе тела и направлено в сторону равнодействующей силы.
Это утверждение является основным законом динамики — вторым законом Ньютона.
Формула, выражающая математическую запись этого закона, подчёркивает, что сила является причиной, а ускорение — следствием. Поэтому её часто называют уравнением движения тела.
Второй закон Ньютона — это фундаментальный закон природы, которому с удивительной точностью подчиняются движения макроскопических тел: от маленьких снежинок до огромных космических объектов.
Обратим ваше внимание на то, что второй закон Ньютона выполняется только для материальных точек, движущихся в инерциальных системах отсчёта.
Теперь давайте мы с вами более подробно поговорим о массе. Что нам о ней известно на данный момент?
Во-первых, это то, что масса является количественной мерой инертности тел.
А во-вторых, мы знаем, что единицей массы в СИ является килограмм, эталон которого выполнен из сплава платины и иридия.
Имея на руках эталон килограмма, мы с вами можем определить массу любого тела, например, с помощью рычажных весов. Ведь очевидно, что если какое-либо тело, располагающееся на одной чашке весов, уравновешивает эталон, то его масса равна одному килограмму. Теперь мы можем измерять тело массой два килограмма и так далее.

Если мы разделим эталон на две равные части, то получим два тела по 500 грамм каждое, которые тоже можно использовать для измерения. А разделив пополам одно из таких тел, мы получим ещё меньшие массы и так далее.
В рассмотренном примере измерение массы основано на том, что на тела действует сила притяжения Земли. Поэтому измеряемую таким способом массу называют гравитационной массой.
Измерить массу тела также можно на основе явления инерции. Мы уже с вами знаем, что ускорение прямо пропорционально силе, действующей на тело, и обратно пропорционально его массе. Тогда, если на любых два тела действуют одинаковые силы, то отношение их масс равно обратному отношению ускорений:
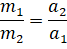
Из формулы видно, что если есть тело известной массы, то, измерив ускорения этого тела и тела с неизвестной массой, движущихся под действием одинаковых сил, легко найти неизвестную массу:
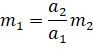
Определяемая таким способом масса называется инертной массой.
Многочисленные опыты показали, что гравитационная масса равна массе инертной.
Также в классической механике Ньютона считают, что:
· масса тела не зависит от скорости его движения;
· масса тела равна сумме масс всех частиц (или материальных точек), из которых оно состоит;
· и для данной системы тел выполняется закон сохранения массы: при любых процессах, происходящих в системе тел, её масса остаётся неизменной.
Для закрепления материала решим с вами небольшую задачу. Тело массой 50 кг тянут по горизонтальному участку пути, прикладывая силу под углом 60о к горизонту. Модуль прикладываемой силы равен 200 Н), а модуль силы трения скольжения — 100 Н. Определите модуль ускорения тела.

Домашнее задание: выучить пар. 21-22, А2 на стр.79 и №3 на стр.82 выполнить письменно, проработать ссылку: https://www.youtube.com/watch?v=msqK-5pg76k&list=PLvtJKssE5NrjCwT9X0Pty3ZIgb0fFLUsZ&index=10