СОДЕРЖАНИЕ
СОДЕРЖАНИЕ. 2
ВВЕДЕНИЕ. 3
1 ПОНЯТИЕ МНОЖЕСТВА.. 4
1.1 Определение множества. 4
1.2 Способы задания множества. 6
1.3 Подмножества. 7
2 ОПЕРАЦИИ НАД МНОЖЕСТВАМИ.. 8
2.1 Объединение. 8
2.2 Пересечение. 9
2.3 Разность. 10
Заключение. 11
Список использованной литературы.. 12
ВВЕДЕНИЕ
Теория множеств как математическая дисциплина создана Кантором. Теория множеств стала основой многих разделов математики — общей топологии, общей алгебры, функционального анализа и оказала существенное влияние на современное понимание предмета математики. В первой половине XX века теоретико-множественный подход был привнесён и во многие традиционные разделы математики, в связи с чем стала широко использоваться в преподавании математики, в том числе в школах.
Людям постоянно приходится иметь дело с различными совокупностями предметов, что повлекло за собой возникновение понятия числа, а затем и понятия множества, которое является одним из основных простейших математических понятий и не поддается точному определению.
Множества это – специальная самостоятельная тема, которая относится к области основ математики.
Множества как тип данных оказались очень удобными для программирования сложных жизненных ситуаций, так как с их помощью можно точно моделировать объекты реального мира и компактно отображать сложные логические взаимоотношения.
Интуитивно под множеством понимается совокупность определенных, вполне различимых объектов, рассматриваемых как единое целое. Как правило, термин множество объясняется с помощью примеров, а потом указываются правила его использования в математических применениях.
.
1 ПОНЯТИЕ МНОЖЕСТВА
1.1 Определение множества
Множество не имеет точного определения, и его следует отнести к аксиоматическим понятиям. Одним из наиболее устоявшихся определений множества является следующее: под множеством понимают любое собрание определённых и отличных друг от друга объектов, мыслимых как единое целое. Создатель теории множеств немецкий математик Георг Кантор (1845-1918) говорил так: "Множество есть многое, мыслимое нами как целое".
В математике изучаются множества чисел, например, состоящие из всех:
- натуральных чисел 0, 1, 2, 3, 4,...
- простых чисел
- чётных целых чисел
Универсальность этого понятия в том, что под него можно подвести любую совокупность предметов. Здесь годится все – марки, числа, люди, точки, звезды, тигры, векторы, функции и т.д. Даже сами множества могут объединяться во множества. Например, математики говорят про множество фигур на плоскости, про множество тел в пространстве, но каждую фигуру, каждое тело они представляют как множество точек.
Следует подчеркнуть, что о множестве можно вести речь только тогда, когда элементы множества различимы между собой. Например, нельзя говорить о множестве капель в стакане воды, т.к. невозможно четко и ясно указать каждую отдельную каплю.
Множества, все элементы которого являются числами, называются числовыми множествами. Множества, элементами которого являются другие множества, называются классом или семейством.
Для ряда числовых множеств в математике приняты стандартные обозначения:
- N – множество натуральных чисел;
- Z – множество целых чисел;
- Q – множество рациональных чисел;
- R – множество действительных чисел;
- C – множество комплексных чисел.
Множество, не содержащее ни одного элемента, называется пустым множеством. Например, множество всех действительных корней уравнения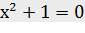 
есть пустое множество. Пустое множество в дальнейшем будем обозначать через Æ.
Например, множество русских слов, начинающихся на букву Ъ. Таких слов нет, поэтому это пустое множество, численность его элементов равна нулю.
Таким образом, когда мы говорим о множестве, то объединяем некоторые объекты в одно целое, а именно в множество, элементами которого они являются.
1.2 Способы задания множества
Существует два основных способа задания множества: перечисление и описание.
Например, множество отличников группы можно задать, перечислив студентов, которые учатся на “отлично”. Например: {Иванов, Сидоров, Петров,…}. Для сокращения записи А={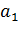 
, 
, … 
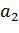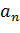} вводят множество индексов I={1,2,….n} и пишут А={ 
}.
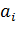Если множество бесконечно, то его элементы перечислить нельзя. В таких случаях указывают характеристическое свойств о его элементов.
Характеристическое свойство – это такое свойство, которым обладает каждый элемент, принадлежащий множеству, и не обладает ни один элемент, который ему не принадлежит.
А={х|P(x)}–множество А состоит из элементов х, удовлетворяющих свойству Р(х). Например, если А состоит из точек интервала 1 < х ≤ 2, то запишем: А={x| 1< х ≤ 2}.
| Q A |
| 1 2 3 4 5 |
В математике приходится постоянно сталкиваться с бесконечными множествами (нельзя сказать, сколько элементов в этих множествах, нельзя их полностью перебрать). Например: множества натуральных, целых, четных, нечетных чисел и многие другие.
1.3 Подмножества
При факторном рассмотрении множества могут выделяться его отдельные части. Это называется выделением подмножеств:
Множество В называется подмножеством множества А, если все элементы В принадлежат и А: В Ì А – В включено (или содержится) в А. Если хотя бы один элемент В не содержится в А, то B Ë A – В не подмножество (не включено в) А. (см. рисунок 1.1.).
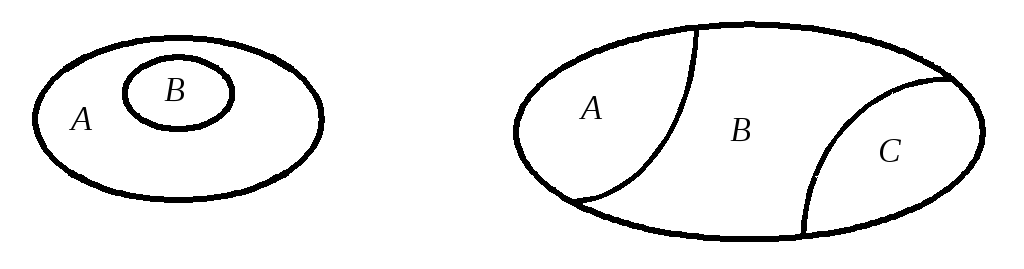
Рисунок 1.1 - Подмножества
Считают, что каждое множество А является подмножеством самого себя. A Ì A.
Любое непустое подмножество В множества А, не совпадающее со множеством А, называется собственным подмножеством. Для множества А пустое множество Æ и само множество А называются несобственнымиподмножествами множества А. Множество, которое включает все рассматриваемые множества, называется универсальным. Обозначается U.
Любое множество можно изобразить графически, нарисовав замкнутый контур и представив себе, что элементы этого множества изображены точками, находящимися внутри этого контура. Показывать на рисунке точки не обязательно. Универсальное множество изображается в виде прямоугольника. Такой способ изображения множеств носит название диаграмм Венна (или кругов Эйлера). Чаще называется диаграммами Эйлера-Венна.
ОПЕРАЦИИ НАД МНОЖЕСТВАМИ
2.1 Объединение
Объединением (суммой) двух множеств А и В называется множество, состоящее из всех элементов, принадлежащих хотя бы одному из данных множеств. Объединение записывается как:
AÈB={x:xÎ А или хÎ В или обоим множествам}
Если представить множества А и В при помощи кругов Эйлера, то объединение данных множеств изобразится заштрихованной областью (см. рисунок 2.1.).
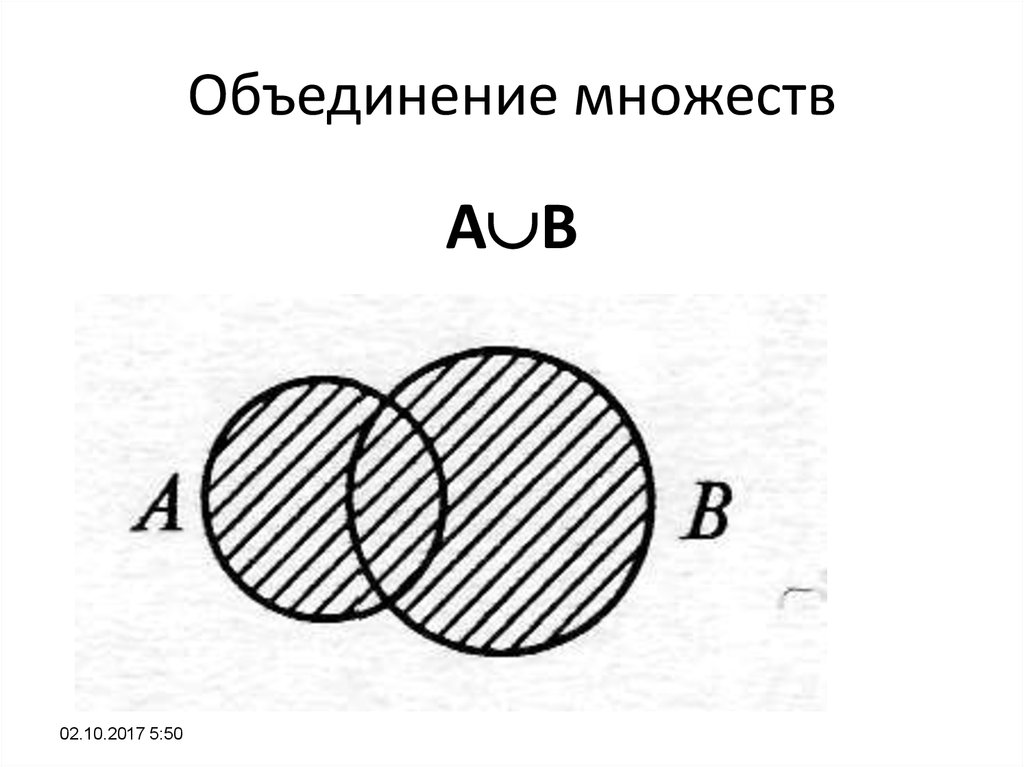
Рисунок 2.1 - Объединение
Пример:
Пусть А={1,3,6,8} и В={2,4,6,8}, тогда Объединение А и В есть АÈВ={1,2,3,4,6,8}. При этом элементы 6 и 8 принадлежат обоим множествам.
Аналогично определяется объединение более чем двух множеств. Объединение трех множеств АÈВÈС, каждый, из элементов которого принадлежит хотя бы одному из множеств А, В и С:
АÈВÈС={х:хÎА или хÎВ или хÎС}
Объединение множества положительных чётных чисел и множества положительных нечётных чисел является множество натуральных чисел.
Если в выражении есть С и Е множеств, но нет скобок, то сначала выполняют С.
2.2 Пересечение
Пересечением множеств А и В называется множество, состоящее из элементов, которые принадлежат множествам А и В одновременно.
Пересечение записывается как:
АÇВ={х:хÎ А хÎ В}
Если представить множества А и В при помощи кругов Эйлера, то пересечение данных множеств изобразится заштрихованной областью (см. рисунок 2.2)
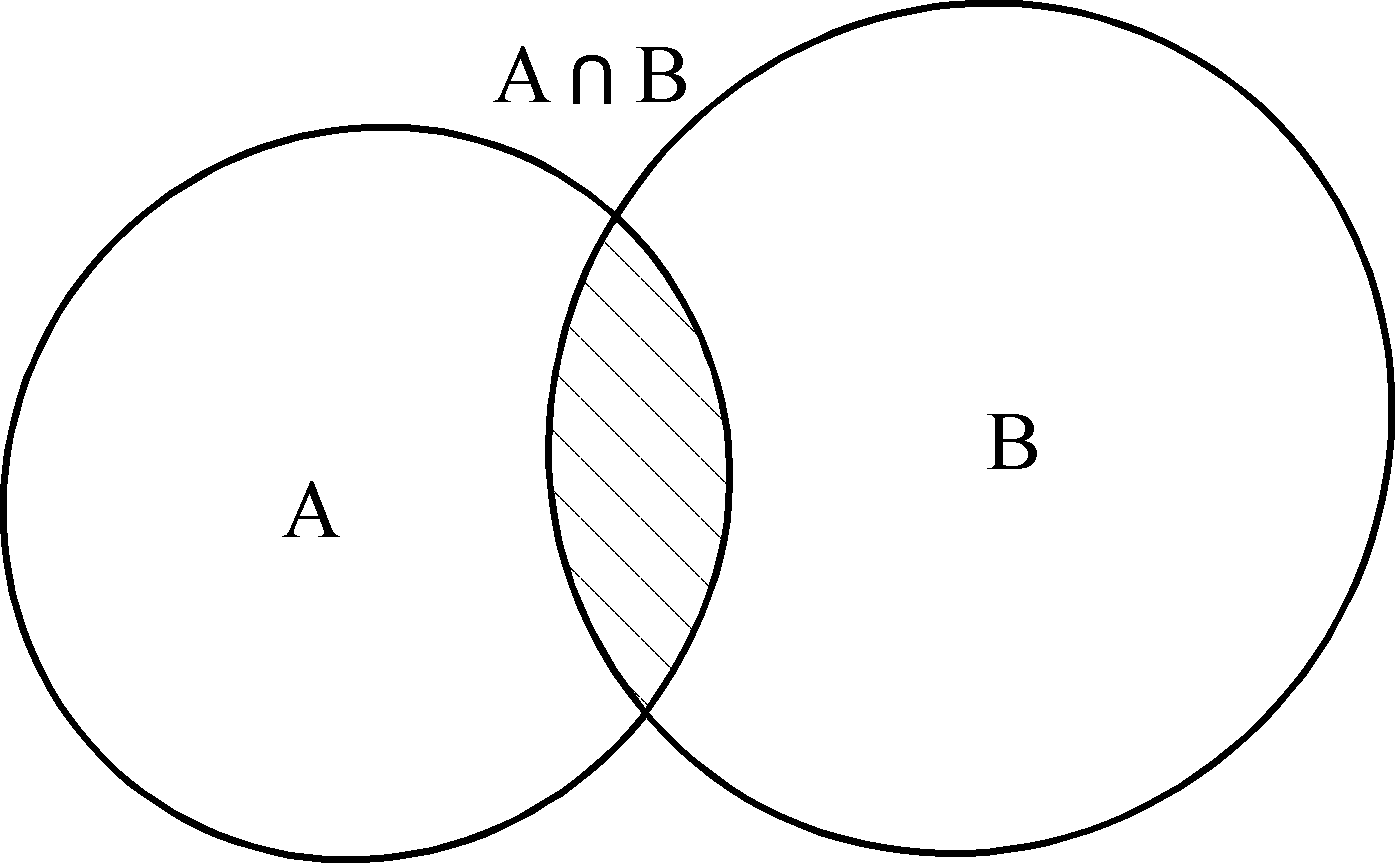
Рисунок 2.2 - Пересечение
Пример:
А={1,2,3,4,5}; В={4,5,6,7}
АÇВ={4,5}
Пересечение более чем двух множеств определяется аналогичным образом. Пересечение трех множеств А, В и С есть множество элементов, которые принадлежат А, В и С: АÇВÇС={х:хÎ А и хÎ В и хÎ С}.
Если множеств А и В не имеют общих элементов, то их пересечение пусто: АÇВ=Æ. Такие множества А и В называются непересекающимися.
Пусть А – множество целых положительных чисел, а В – множество целых отрицательных чисел. Тогда А и В – непересекающиеся множества, так как не существует целых чисел, которые были бы одновременно и положительными, и отрицательными.
2.3 Разность
Разностью двух множеств А и В называется множество, элементами которого являются те и только те элементы множества А, которые не принадлежат В. При этом предполагается, что множество В не является частью множества А. Разность множеств А и В обозначается А/В и по определению А/В={х:хÎ А и хÏ В}. Таким образом, при вычитании множества В из множества А из А удаляют пересечение А и В:
А/В=А/(АÇВ).
Пример:
Пусть А – множество студентов данной группы института, В – множество девушек, обучающихся в этом институте, тогда А/В – множество всех юношей, обучающихся в данной группе этого института.
Пусть а={1,5,9,10}, В={1.3,8,9}, тогда А/В={5,10} и В/А={3,8}.
В случае, когда В – часть множества А, А/В называют дополнением к B в множестве А и обозначают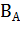 
.
Пример:
Пусть В – множество четных чисел, А – множество целых чисел, тогда 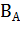– множество нечетных чисел.
Часто все множества, с которыми имеют дело в том или ином рассуждении, являются подмножествами некоторого определенного фиксированного множества. Это множество называют универсальным и обозначают U.
Заключение
Тема моего проекта: «Применение понятия множества». Мы рассмотрели основные понятия множества, а также способы его задания, подмножества и операции над множествами. Кроме того, в моей проектной работе даны такие определения, как: непересекающиеся множества, универсальное множество, собственное подмножество, характеристическое свойство, пустое множество и т.д.
Теория множеств может быть активно использована на практике и в теории управления системами, в финансах и экономике для решения задач при условии неопределенности основных показателей. Например, такая техника, как фотоаппараты и некоторые стиральные машины, оборудована нечеткими контроллерами. Также множества как тип данных оказались очень удобными для программирования сложных жизненных ситуаций, так как с их помощью можно точно моделировать объекты реального мира и компактно отображать сложные логические взаимоотношения. Множества применяются в языке программирования Паскаль.
Таким образом, мы убедились, что теория множеств имеет важное прикладное значение и может применяться в различных областях.
Список использованной литературы
1. Аматова Г.М. Математика: в 2 кн. Кн. 2: учеб. Пособие для студ. высш. пед. учеб. заведений / Г.М. Аматова, М.А. Аматов. – М.: Издательский центр «Академия», 2008. – 240 с.
2. Истомина Н.Б. Математика: учимся решать комбинаторные задачи (1-3 кл.)/ – Ассоциация XXI век, 2014.
3. К. Куратовский, А. Мостовский. Теория множеств / Перевод с английского М. И. Кратко под редакцией А. Д. Тайманова. — М.: Мир, 1970. — 416 с.
4. Петерсон Л.Г. Математика. Учебники для 1–4 классов. – М., 2000.
5. Стойлова Л.П. Математика: Учеб. пособие для студ. высш. пед. учеб.заведений М.: Издательский центр «Академия», 2004. – 424 с.
6. Столл Р. Р. Множества. Логика. Аксиоматические теории. / Перевод с английского Ю. А. Гастева и И. Х. Шмаина под редакцией Ю. А. Шихановича. — М.: Просвещение, 1968. — 232 с.
7. Столяр А.А., Лельчук М.П. Математика. – Минск, 1975.