Часть 4. Дифференциальные уравнения
Глава 12.
Элементы общей теории обыкновенных
Дифференциальных уравнений
Задачи, приводящие к дифференциальным уравнениям
Дифференциальное исчисление позволяет исследовать свойства заданной функции. Обратная задача состоит в нахождении неизвестной функции по ее заданным свойствам. При решении таких задач мы приходим к уравнениям, связывающим неизвестную функцию и ее производные различных порядков. Такие уравнения называются дифференциальными. Примером задачи, приводящей к дифференциальным уравнениям, может служить следующая задача.
Скорость распада радия пропорциональна конечному количеству радия. Найти закон, выражающий изменение количества радия с течением времени.
Решение. 
- количество радия в момент времени 
.
- скорость изменения количества радия.
По условию 
, где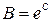 
. Если в момент времени 
имелось 
радия, то 
. Окончательно 
.
Обыкновенные дифференциальные уравнения и их решения
Обыкновенным дифференциальным уравнением называется уравнение, связывающее независимую переменную, неизвестную функцию этой переменной и ее производные различных порядков.
Порядком дифференциального уравнения называется наивысший порядок входящих в него производных. Например, 
-обыкновенное дифференциальное уравнение второго порядка.
Общий вид обыкновенного дифференциального уравнения 
-го порядка: 
, где 
некоторая функция 
переменных.
Определение. Всякая функция 
, при подстановке которой обыкновенное дифференциальное уравнение обращается в тождество, называется решением этого дифференциального уравнения.
Например, решением дифференциального уравнения 
является функция 
; т.к. 
, т.е. 
.
Всякое обыкновенное дифференциальное уравнение имеет, вообще говоря, бесконечное множество решений. Например, дифференциальное уравнение наряду с решением имеет решение 
, где 
-произвольная постоянная. Позднее увидим, что для обыкновенного дифференциального уравнения 
-го порядка существует решение, содержащее произвольных постоянных. Такое решение называется общим решением. Например, для дифференциального уравнения решение 
является общим решением. Придавая произвольным постоянным общего решения различные числовые значения, будем получать частные решения дифференциального уравнения. Частное решение дифференциального уравнения не содержит произвольных постоянных.
Операцию нахождения решений дифференциального уравнения называют интегрированием дифференциального уравнения. Взятие интеграла будем называть квадратурой. Общее решение дифференциального уравнения, особенно если оно записано в неявной форме, часто называют общим интегралом.
График решения дифференциального уравнения называю интегральной кривой этого дифференциального уравнения. Общее решение, например, дифференциального уравнения первого порядка содержит произвольную постоянную. Значит, ему соответствует бесконечное множество интегральных кривых 
. Каждому значению 
соответствует определенная кривая этого семейства. Говорят, что уравнение , 
, задает однопараметрическое семейство кривых.
Пусть дифференциальное уравнение первого порядка задано в виде
(1)
где 
определена в некоторой области 
. Это уравнение ставит в соответствие каждой точке 
определенное значение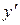 
. Иначе говоря, уравнение (1) задает в каждой точке области 
некоторое направление, совпадающее с направлением касательной к интегральной кривой, проходящей через эту точку. Совокупность этих направлений называется полем направлений уравнения (1). Для наглядного изображения поле направлений в каждой точке области проводят отрезок с угловым коэффициентом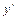 
.
Задачу интегрирования дифференциального уравнения (1)теперь можно поставить так: найти каждую кривую, чтобы ее касательная в каждой точке имела направление, совпадающее с направлением поля в этой точке.
При построении поля направлений удобно рассматривать геометрические места точек, в которых 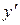имеет постоянное значение. Множество таких точек называют изоклинами.
Пример. 
. Если 
, то 
, т.е. 
. Так как угловые коэффициенты поля и прямых связаны соотношением 
, то направление поля перпендикулярно изоклине в любой точке. Значит, интегральные кривые – концентрические окружности с центрам в начале координат. Поле направлений иногда используют для приближенного определения интегральных кривых.
Начальные условия
Пусть дано дифференциальное уравнение первого порядка . Его общее решение содержит одну произвольную постоянную: 
. Часто требуется найти то частное решение которое при 
принимает значение 
. Эти условия называются начальными условиями. Чтобы удовлетворить начальным условиям, нужно определить соответствующее значение постоянной 
. Начальные условия записывают: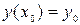 
или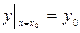 
.
Частное решение, удовлетворяющее начальным условиям, называется решением с начальными условиями. Ему соответствует интегральная кривая, проходящая через точку 
.
Пример. 
. Общее решение 
. Частное решение 
проходит через точку 
.
Общее решение дифференциального уравнения второго порядка содержит две произвольных постоянных: 
. Здесь соответственно нужно иметь две пары условий: найти то частное решение, которое при принимает значение 
и имеет производную 
. Пишут 
или 
.
Для определения значений произвольных постоянных 
и 
продифференцируем общее решение и решим систему 
.
Общее решение дифференциального уравнения -го порядка содержит произвольных постоянных: 
. Их можно найти, если иметь условий 
. Соответствующие значения постоянных находим из системы
Задачу нахождения решения дифференциального уравнения , удовлетворяющего начальным условиям 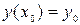, называют задачей Коши (аналогично и для дифференциального уравнения порядка 
, 
).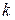