Лабораторная работа № 4
Определение ускорения свободного падения с помощью
математического маятника
Цель: определить ускорение свободного падения с помощью математического маятника.
Оборудование, средства измерения: 1) штатив с держателем; 2) шарик с нитью; 3) пробка
с прорезью в боковой поверхности; 4) секундомер; 5) измерительная линейка;
6) штангенциркуль.
Теоретическое обоснование:
Для измерения ускорения свободного падения применяются маятниковые приборы. С их помощью удается измерить ускорение свободного падения с абсолютной погрешностью порядка 10-5м/с2.
В работе используется простейший маятник – шарик на нити. Если отклонить маятник от точки О в точку А, т.е. от положения равновесия, на угол a и отпустить, то он будет колебаться (рис.1). Маятник совершит полное колебание, если он из точки А перейдёт в точку В и вернётся обратно. Время полного колебания называют периодом.
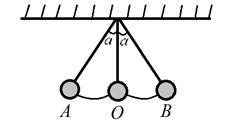
Рис. 1
При малых размерах шарика по сравнению с длиной нити и небольших отклонениях (50-100) от положения равновесия период колебаний равен периоду колебаний математического маятника:
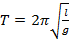
Из формулы видно, что период колебаний математического маятника не зависит от массы подвешенного груза и амплитуды колебаний.
Для увеличения точности измерения периода нужно измерить время t достаточно большого числа n полных колебаний маятника. Тогда период:
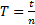
и ускорение свободного падения может быть вычислено по формуле:
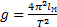
Порядок выполнения работы:
1. Поместите штатив с держателем на край стола.
2. Укрепите свободный конец шарика в прорези и зажать в держателе.
3. Измерьте диаметр шарика штангенциркулем: dш =
длину нити линейкой: 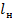 1 =
1 =
4. Отклоните шарик на небольшой угол (5-100) (примерно на 5 см) и отпустить. По секундомеру определить время, t1= с, за которое маятник совершит n полных колебаний, например, 50.
5. Вычислите период колебаний математического маятника:
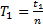
6. Используя формулу периода колебаний математического маятника
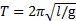 , вычислите ускорение свободного падения:
, вычислите ускорение свободного падения:
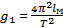 , где l= lн + dш/ 2.
, где l= lн + dш/ 2.
7. Опыт повторите 2 раза, меняя длину маятника (протягивая нить через пробку) и число полных колебаний его.
t2=
n2=
T2=
lн2=
l2=
g2=
8. Определите среднее значение:
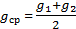
9. Сравните результаты опыта с табличным значением ускорения свободного падения для данной географической широты gт= 9,816 м/с2.
10. Найдите относительную погрешность:
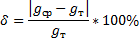
11. Результаты всех измерений и вычислений занесите в таблицу.
| № | Длина нити | Диаметр шарика | Длина маятника | Число полных колебаний | Время полных колебаний | Период полного колебания | Ускорение свободного падения | Среднее значение ускорения свободного падения | Относительная погрешность |
| lн | dш | l | n | t | T | g | gср | d | |
| м | м | м | с | с | м/с2 | м/с2 | % | ||
| 1. | |||||||||
| 2. |
Вывод:
Контрольные вопросы:
1. Подтвердил ваш эксперимент теоретически предсказанную зависимость частоты колебаний математического маятника от его длины?
2. Будет ли верным выражение: 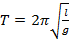 для определения частоты колебаний маятника при больших углах отклонения от положения равновесия?
для определения частоты колебаний маятника при больших углах отклонения от положения равновесия?
3. Чему равно ускорение свободного падения?
4. Где находят применение маятники?