Практическая работа 13
Признаки взаимного расположения прямых. Угол между прямыми. Взаимное расположение прямых и плоскостей
Цель работы: Обеспечить закрепление аксиом стереометрии и их следствий
Дидактический материал для выполнения практической работы:
Методические рекомендации для выполнения практических работ, тетрадь для практических работ, конспект лекций.
Задание:
1. Прямые а и b пересекаются в точке О, А а, В b, Р АВ. Докажите, что прямые а и b и точка Р лежат в одной плоскости.
2. На данном рисунке плоскость содержит точки А, В, С, Д, но не содержит точку М. Постройте точку К – точку пересечения прямой АВ и плоскости МСД. Лежит ли точка К в плоскости.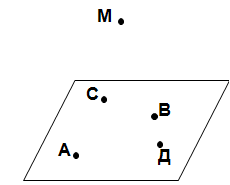 
Вариант 1.
1.Прямая а, параллельная прямой b, пересекает плоскость α. Прямая с параллельна прямой b, тогда:
а) прямые а и с пересекаются; б) прямая с лежит в плоскости α;
в) прямые а и с скрещиваются; г) прямые а и с параллельны.
2. Каким может быть взаимное расположение прямых а и b, если через прямую а можно провести плоскость, параллельную прямой b?
а) скрещиваются или пересекаются;
б) скрещиваются или параллельны;
в) только скрещиваются;
г) только параллельны.
3. Прямые а и в лежат в параллельных плоскостях, следовательно эти прямые
а) скрещиваются или пересекаются; б) скрещиваются или параллельны;
в) только скрещиваются; г) только параллельны.
Каким может быть взаимное расположение двух прямых, если обе они параллельны одной плоскости?
а) только параллельны; б) все случаи взаимного расположения;
в) только скрещиваются; г) только пересекаются.
5. Прямая а параллельна плоскости α. Какое из следующих утверждений верно?
а) Прямая а параллельна любой прямой, лежащей в плоскости α;
|
|
б) прямая а не пересекает ни одну прямую, лежащую в плоскости α;
в) прямая а скрещивается со всеми прямыми плоскости α;
г) прямая а имеет общую точку с плоскостью α.
6. Плоскость проходит через середины боковых сторон АВ и CD трапеции ABCD – точки М и N.
а) Докажите, что AD || плоскости.
б) Найдите ВС, если AD = 10 см, MN = 8 см.
7. Прямая MA проходит через вершину квадрата ABCD и не лежит в плоскости квадрата.
Докажите, что МА и ВС – скрещивающиеся прямые.
8. Точка М не лежит в плоскости трапеции ABCD (AD || BC).
а) Докажите, что треугольники МАD и МВС имеют параллельные средние линии.
б) Найдите длины этих средних линий, если AD: BC = 5: 3, а средняя линия трапеции равна 16 см
Вариант 2
1.Прямая с, параллельная прямой а, пересекает плоскость β. Прямая b параллельна прямой а, тогда:
а) прямые b и с пересекаются; б) прямая b лежит в плоскости β;
в) прямые b и с скрещиваются; г) прямые b и с параллельны.
2.Каким может быть взаимное расположение прямых а и b, если любая плоскость, проходящая через а, не параллельна b?
а) скрещиваются; б) параллельны; в) пересекаются; г) определить нельзя.
3.Прямые а и в лежат в параллельных плоскостях, следовательно эти прямые
а)скрещиваются или пересекаются; б) скрещиваются или параллельны;
в) только скрещиваются; г) только параллельны.
4.Прямая а параллельна плоскости α. Какое из следующих утверждений верно?
а) Прямая а параллельна любой прямой, лежащей в плоскости α;
б) прямая а не пересекает ни одну прямую, лежащую в плоскости α;
в) прямая а скрещивается со всеми прямыми плоскости α;
|
|
г) прямая а имеет общую точку с плоскостью α.
5.Каким может быть взаимное расположение прямых а и b, если прямая а лежит в плоскости α, а прямая b параллельна этой плоскости?
а) Параллельны или пересекаются;
б) скрещиваются или пересекаются;
в) параллельны или скрещиваются;
г) определить нельзя.
6. Плоскость проходит через основание AD трапеции ABCD. M и N – середины боковых сторон трапеции.
а) Докажите, что MN || плоскости.
б) Найдите AD, если ВС = 4 см, MN = 6 см.
7. Прямая CD проходит через вершину треугольника АВС и не лежит в плоскости АВС. E и F – середины отрезков АВ и ВС.
Докажите, что CD и EF – скрещивающиеся прямые.
8. Треугольник АВС и трапеция KMNP имеют общую среднюю линию EF, причем KP || MN, EF || AC.
а) Докажите, что АС || К Р.
б) Найдите КР и MN, если КР: MN = 3: 5, AC = 16 см.
Требования к отчету:
Отчет должен содержать решение заданий с указаниями на теоретические факты, использованные при решении.
Теоретические положения.
А1. Через любые три точки, не лежащие на одной прямой, проходит плоскость, и притом только одна.
| А   В (точки А, В, С лежат в плоскости ) С
|
А2. Если две точки прямой лежат в плоскости, то все точки прямой лежат в этой плоскости
| АB  Прямая АВ лежит в плоскости
|
Замечание. Если прямая и плоскость имеют только одну общую точку, то говорят, что они пересекаются.
а  =М Прямая а и плоскость пересекаются в точке М.
| |
|
А3. Если две плоскости имеют общую точку, то они имеют общую прямую, на которой лежат все общие точки этих плоскостей.
| и  пересекаются по прямой а.
|
Следствие 1. Через прямую и не лежащую на ней точку проходит плоскость, и притом только одна.
|
|
Следствие 2. Через две пересекающиеся прямые проходит плоскость, и притом только одна.
Критерии оценки
Все этапы заданий выполнены верно, логически грамотно, нет неточностей – оценка 5; оценка 4 ставится, если была допущена неточность или не указана аксиома или ее следствие, которые использованы при решении задач; если была допущена серьезная ошибка, повлекшая неверный ответ, то ставится оценка 3, во всех остальных случаях ставится оценка 2.