Т.е. с помощью криволинейный интеграл по замкнутому контуру L можно вычислить площадь области ограниченный данным контуром.

Приложение криволинейных интегралов.

1. Некоторые приложения криволинейного интеграла I рода.

а. Длина кривой

Если подынтегральная функция тождественно равна единице, то интеграл равен длине плоской или пространственной линии АВ:

б. Площадь цилиндрической поверхности.

Если цилиндрическая поверхность, каждая образующая которой параллельна оси Oz имеет своей направляющею линию АВ, лежащую в плоскости хОу, то площадь поверхности z=f(x,y) равен

в. Масса плоской кривой

Если АВ материальная кривая, а функция γ=γ(х,у) непрерывно дифференцируемая в каждой точке данной кривой, задает функцию распределения плотность, то масса всей плоскости или пространственной линии есть:

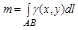
г. Статические моменты, центр тяжести.

Статические моменты относительно осей Ох и Оу определяются равенством:

Координаты центра тяжести данной кривой равны:

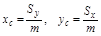
д. Моменты инерции.

Моменты инерции кривой АВ относительно осей Ох, Оу и начала координат соответственно равна

 

Формула Остроградского–Грина

Пусть в плоскость хОу задания правильная в направлении осей область D, ограниченная контуром L=AnBmA. Установим связь между двойным интегралом по области D и криволинейным по границе L.

Теорема1. Если функции Х(х,у) и Y(х,у) непрерывны вместе со своими частными производными и в некоторой области D ограниченной кривой L, то имеет место формула.

Доказательство: Пусть дуги АnB и AmB заданные уравнениями:

АnB: , AmB:

Двойной интеграл в формуле Остраградского–Грина, можно разбить на разность двух интегралов. Рассмотрим один из них:

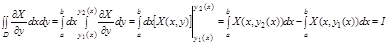
Заменим данные определенные интегралы соответствующим криволинейным:

Аналогично выводится, что

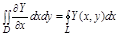теорема доказана.

Замечание. Из свойств двойного интеграла известно, что если подынтегральная функция тождественно равна единицы, то интеграл равен площади области D, т.е. если

то из формулы Остроградского–Грина получим:

Т.е. с помощью криволинейный интеграл по замкнутому контуру L можно вычислить площадь области ограниченный данным контуром.

 

Пример. Вычислить криволинейный интеграл

, где L –контур прямоугольника с вершинами A(3,2), B(6,2), C(6,4), D(3,4).

1. ,

2.

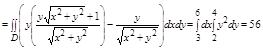
3. Условия независимости криволинейного интеграла II рода от пути интегрирования.

Пусть криволинейный интеграл II рода не зависит от пути интегрирования, а зависит только от положения начальной и конечной точек А и В. В этом случае:

Изменяя направление интегрирования во втором интеграл получим:

Таким образом, из условия независимости криволинейного интеграла от пути интегрирования следует равенство нулю криволинейного интеграла по любому замкнутому контуру соединяющие точки А и В и лежащему в области D.

Теорема 2. Для того чтобы криволинейный интеграл

не зависел от пути интегрирования в односвязной (без дыр) области D, в которой функции Х(х,у) и Y(х,у) непрерывны вместе со своими производными, необходимо и достаточно, чтобы выполнилось условие:

Доказательство: Из формулы Остроградского–Грина и предыдущих рассуждений имеем, что для независимости криволинейного интеграла II рода от пути интегрирования необходимо

Теорема доказана.

Если криволинейный интеграл II рода не зависит от пути интегрирования, то достаточно зафиксировать его начальную точку и конечную , записывают:

Пример. Вычислить .

1. , а следовательно данный интеграл не зависит от пути интегрирования, тогда, пусть АВ есть прямая: , тогда

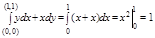
Следствие. Если выполняется условие то выражение , по ранее полученным выкладкам при решении дифференциальных уравнений является полными дифференциалом некоторой функции U=U(x,y), т.е.

и следовательно

т.е. криволинейный интеграл II рода, независящий от пути интегрирования, соединяющего точки А и В, равен разности значений функции в этих точках.

Замечание.

1. Чтобы не спутать переменную интегрирования х с верхним пределом х, переменную интегрирования следует обозначить иначе.

2. Функцию U=U(x,y) удовлетворяющую условию

можно найти используя формулу . В качестве начальной точки обычно берут точку (0,0).

Т.к. криволинейный интеграл не зависит от пути интегрирования, выберем путь параллельный осями координат, при этом

3. Аналогичный результат справедлив и для криволинейного интеграла

по пространственной кривой, при этом условие независимости интеграла от пути интегрирования формулируются

Пример: Найти функцию, заданную своим полным дифференциалом

1.

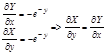
2.

4. Приложение криволинейного интеграла II рода.

В процессе рассмотрения криволинейного интеграла II рода мы пришли к некоторым его приложениям:

а. Площадь плоской фигуры.

Площадь области D плоскости хОу ограниченной линией L можно найти по формуле

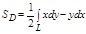
Пример. Найти площадь фигуры, ограниченной астроидой , .

1.

, при

2.

б. Работа переменной силы.

Работа при перемещении точки из положения А в положение В под действием силы 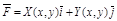вычисляется по формуле:

Пример. Найти работу силы вдоль кривой от точки О(0,0) до точки В(1,1).

1.

, при

2.

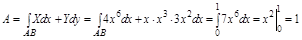
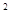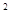Пример. Найти работу силы по перемещению материальной точки из положения M(R;0) в положение N(–R;0) вдоль кривой L: x +y =R 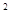(y=>0)

1.

2. Зададим уравнение линии параметрически: x=Rcos t, y=Rsin t, используя уравнения линии, преобразуем криволинейный интеграл в обыкновенный с переменной t: dx=–R sintdt, dy=R 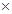costdt