Группа №21. Математика.
№41 27.10.2020
Отработать материал в домашних тетрадях, выполнить домашнее задание, сфотографировать (скан.) отправить на электронную почту преподавателя m.kayuck@yandex.ua
Учебник геометрии 10-11 класс Атанасян Л.С. и др.
https://school-zaozernoe.ru/files/10-11_kl._geometriya._atanasyan_l.s._i_dr_2013_-255s.pdf
Тема: Параллельность прямой и плоскости в пространстве.
Цели: ввести определение параллельности прямой и плоскости в пространстве. Рассмотреть признак параллельности прямой и плоскости в пространстве.
Способствовать развитию внимания, пространственного воображения, умению анализировать, применять знания в стандартных ситуациях.
Воспитывать интерес к изучению математики, развивать культуру письменной математической речи.
Прямая и плоскость называются параллельными, если они не имеют общих точек.
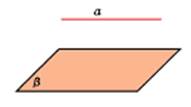
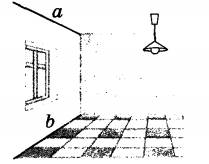
Наглядный пример, который дает представление о прямой, параллельной плоскости- это линия пересечения стены и потолка - она параллельна плоскости пола.
(Прочитать) Геометрия, которую мы изучаем, называется евклидовой, по имени древнегреческого ученого Евклида (3 век до нашей эры), который создал целый труд по математике под названием «Начала». В данной книге есть раздел о параллельных прямых.В энциклопедическом словаре слово «параллельность» переводится с греческого языка, как «идущий рядом».В средние века параллельность обозначалась знаком «=». В 1557 году Р. Рекордом для обозначения равенства был введен знак «=», которым мы пользуемся сейчас, а параллельность стали обозначать «║».
В книге «Начала» определение параллельных прямых звучало так «прямые, лежащие в одной плоскости и будучи бесконечно продолжены в обе стороны, ни с той, ни с другой стороны не пересекаются». Это определение почти не отличается от современного.
В области параллельных прямых работало очень много учёных: Н.И. Лобаческий (18-19 век); Аббас ал-Джаухари (работал в Багдаде в 9 веке); Фадл ал-Найризи (Богдад 10 век); Герард (Италия 12 век); Иоганн Генрих Ламберт (Берлин) и многие другие.
Укажем некоторые пары параллельных прямых:
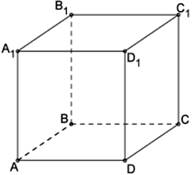
AB||A₁B₁; AB|| CD; A₁B₁||C₁D₁; CD||C₁D₁; AD||A₁D₁; BC||B₁D₁; AD||BC; A₁D₁||B₁C₁.
А теперь рассмотрим некоторые пары скрещивающихся прямых:
AB и A₁D₁; AB и B₁C₁; CD и A₁D₁; CD и B₁C₁; BC и C₁D₁; BC и A₁B₁; AB и B₁C₁;
AB и A₁D₁.
Теорема. Через любую точку пространства, не лежащую на данной прямой, проходит прямая, параллельная данной, и притом только одна.
М и а задают плоскость α
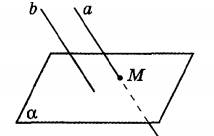
1. Прямая, проходящая через точку М, параллельно прямой а, должна лежать в одной плоскости с точкой М и прямой а, т.е. в плоскости α.
2.В плоскости α через точку М проходит прямая, параллельная прямой а, и притом только одна - это нам известно из курса планиметрии.
3.На чертеже эта прямая обозначена буквой b.
Следовательно, b -единственная прямая, проходящая через точку М параллельно прямой а.
Признак параллельности прямой и плоскости.
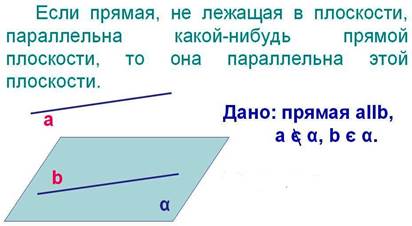
Доказательство.
Доказательство проведем от противного. Пусть a не параллельна плоскости α, тогда прямая a пересекает плоскость в некоторой точке A. Причем A не находится на b, так как a∥b. Согласно определению скрещивающихся прямых, прямые a и b скрещивающиеся.
Пришли к противоречию. Так как согласно данной информации a∥b, они не могут быть скрещивающимися. Значит, прямая a должна быть параллельна плоскости α.
Задача№1.
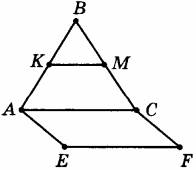
Дано: в ∆ АВС. КМ − средняя линия, КМ=5;
ACFE- параллелограмм.
Найти: EF
Решение
Т.к. КМ − средняя линия, то АС= 2·КМ, то АС=2· 7 = 10
Т.к. ACFE − параллелограмм, то АС=EF= 10
Ответ: EF= 10
Задача№2.

Решение.
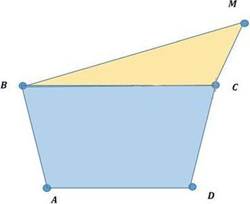


Что и требовалось доказать.
Домашнее задание: §1,п.4,5,6 №26,28