Изменение давления в стволе скважины.

Оптимальное положение для скважин работающих напостоянном давлении в стволе.

Rodolfo Camacho-V., PEMEX/UNAM, Fernando Rodriguez, PEMEX/UNAM, Agustin Galindo-N., IMP/UNAM and Michael Prats, MICHAEL PRATS & ASSOCIATES.

SPE Members

Аннотация

Данная работа рассматривает определение оптимального положения нескольких скважин, работающих с разным постоянным давлением в скважине из двумерных замкнутых пластов, чтобы максимизировать совокупную выработку или общий дебит. Для достижения этой цели мы используем улучшенную версию аналитического решения, недавно предложенного Родригезом и Синколи [1] и алгоритм оптимизации, основанный на квази-ньютоновской процедуре с линейным поиском. На каждой итерации алгоритм аппроксимирует отрицательные значения целевой функции квадратичным соотношением, полученным из ряда Тейлора.

Улучшение решения Родригеса и Синко достигнуто четырьмя способами. Во-первых, достигается аппроксимация, которая работает на ранних временах (до начала периода с преобладанием границы) лучше, чем предыдущее решение. Во-вторых, бесконечные суммы, присутствующие в решении, выражаются в сжатой форме, которая имеет значение для сокращения времени вычисления при использовании алгоритма оптимизации. В-третьих, решение модифицировано, чтобы учесть возможность того, что скважины начинают работать в разное время. Этот вопрос позволяет нам решить проблему получения оптимального положения для программы бурения скважин. Наконец, решение расширяется, чтобы иметь возможность изменить значения давления в стволе или стимулировать любую из скважин в любое время.

Когда скважины работают при различных давлениях, установлено, что оптимальное положение является функцией времени, в противном случае оптимальное положение фиксируется.

 

Введение

Существует два подхода к получению прогноза поведения снижения дебита для скважин, работающих при постоянном давлении: аналитический и эмпирический. Аналитический подход в основном применяется к слегка сжимаемым потокам жидкости [2-6]. Несмотря на это, существуют некоторые исследования, связанные с многофазными системами потока, в течение переходных периодов и периодов с преобладанием границы, как для ламинарных [7-13], так и для неламинарных условий потока, а также для сухих газовых коллекторов [15-20].

Арпс [21] описывает тройку эмпирических кривых снижения. Феткович показал, что эмпирические кривые Арпса могут быть совмещены с решениями [2-4] экспоненциального падения, получая, таким образом, единственный набор типовых кривых для прогнозирования снижения дебита. Камачо и Рагхаван [9] выражали параметры уравнений Арпса с точки зрения физических свойств, а так же указывали условия, при которых могут использоваться эти уравнения.

Тем не менее, мы можем привести некоторые работы (по гомогенным системам) по трещиноватым коллекторам [23-28], скважинам с ГРП [29-30] и слоистым пластам [31-33] с аналитическим подходом, в которых Жанг и другие [34] изучали скважину в составном и нерегулярном пласте.

Несмотря на всю проделанную работу по прогнозированию снижения дебита, большая часть этих исследований была направлена на случай одной скважины. Недавно Родригез и Синко-Лей [1] представили аналитическое исследование для систем с несколькими скважинами. Отличный обзор исследований оптимизации существующих в нефтяной промышленности дается Кэрроллом и Хорном [35].

Рассматриваемая здесь модель учитывает поток жидкости внутри пласта постоянной толщины. Она не учитывает гравитацию и поточные эффекты не связанные с законом Дарси. В Статье 1 было представлено новое аналитическое решение для характеристики работы любого количества скважин с постоянным, но разным давлением в стволе добывающих из прямоугольного замкнутого пласта.

На Рисунке 1 представлено описание системы.

Рис. 1 Система Скважины – Пласт

На Рис.1 предположено, что все скважины начинают работу в одно и то же время и с постоянным состоянием скважины (поврежденным или стимулированным). Было показано, что экспоненциальное падение получается для общего дебита на длительных периодах времени, пока давления поддерживаются постоянными. Было обнаружено, что коэффициент снижения D, одинаков для пласта и для каждой из скважин. Этот коэффициент зависит от размера и формы пласта, количества работающих скважин, положения этих скважин в пласте и от их повреждений. Так же в Статье 1 было показано, что состояние каждой скважины влияет на характеристики работы остальных скважин.

В данной статье мы смягчим некоторые предположения, выдвинутые в Статье 1, мы допустим, что скважины начали работать в разное время, на них может меняться давление в стволе в течении времени их работы и они могут быть простимулированы в любое время. Поэтому, мы разрабатываем более общее аналитическое решение. Цель этой работы показать приложение этих аналитических решений, включив их в алгоритм оптимизации для поиска оптимальных позиций скважин. В некоторых отношениях эта статься является продолжением идей, которые были заложены в Статье 1. Однако, представление этой статьи должно быть самодостаточным, избегая ненужных повторений. Данные, общие для случаев, представленных в этом исследовании, представлены в Таблице 1.

Таблица 1. Параметры Пласта и Скважин

Измерения пласта, футы:

x ₀ = 14000; y₀ =7000

Радиус скважины, футы: 0.25

Начальное давление, psi: 3000

Пористость, доля: 0.15

Проницаемость, мД: 100

Толщина пласта, футы: 100

Сжимаемость нефти, л/psi: 2.Е-05

Объёмный коэффициент заполнения: 1.558

Вязкость нефти, сПз: 0.5364

Результаты

Аналитические модели

Скважины начинают работать в разное время. Используя преобразования Лапласа смещенной функции и следуя Статье 1, мы получаем решения для нескольких скважин, работающих при постоянном, но различном давлении, и при различных временах начала работы на прямоугольном замкнутом пласте, как:

(1)

Где – это Функция Грина сопряженной задачи в пространстве Лапласа и – это безразмерное время на котором j-ая скважина начинает работу.

В данной статье мы используем те же определения безразмерных переменных, что и в Статье 1, т.е.

(2)

и

(3)

Эти определения остаются в силе для безразмерного давления и безразмерного дебита скважины, соответственно. Безразмерные координаты заданы: и . Безразмерное время:

(4)

Для уплотняющих сетку скважин, то есть скважин, начинающих работать в разное время, в месте расположения i-ой скважины, ставят следующее условие:

Где 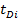– это безразмерное время, на котором скважина начинает работу, – это ступенчатая функция Хевисайда, и 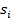– это коэффициент повреждения для i-ой скважины.

Преобразование Лапласа из приведённого выше условия даёт,

(6)

Мы можем использовать теорему о среднем значении для интегралов, чтобы получить:

(7)

Где 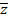- это вещественное число от нуля до единицы. Мы заметили, что 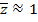даёт хорошие результаты.

Используя (6) и (7) в (1) уравнении, мы получаем следующую систему уравнений в

 

(8)

 

Где: – это безразмерное время, до начала работы i-ой скважины, и

 

(9)

 

С

(10)

И

 

(11)

 

Решая систему уравнений полученную из (8), мы получаем

 

(12)

Где это минор от квадратной матрицы -го порядка имеющей элементы и – определитель матрицы .

Используя аппроксимацию функции Грина на больших временах (дано в приложении А уравнением (А-7)) в (9) и подставляя получившееся уравнение вместе с и в (12), мы получаем

 

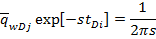
(13)

 

Где: это количество скважин, работающих на момент , , 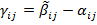задается уравнением (А-8), 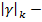определитель матрицы, содержащий как элементы, исключая строку k, которая содержит единицы, это минор и получается путем замены строки k на единицы. И Заметим, что мы использовали вместо (дается в Статье 1) потому, как объясняется в Приложении А, это новое определение функций позволяет конечному выражению конечного дебита работать в более широком диапазоне времени, чем с предыдущим определением, данным в Статье 1.

Инверсия Лапласа выражения (13) дает:

(14)

 

Где

(15)

Безразмерное может быть получено подстановкой долговременной аппроксимацией функции Грина и (А-7) в (1) и перевернём, т.е.

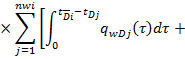
(16)

 

 

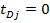Уравнение (14) дает безразмерный дебит j-ой скважины, начинающей работать в момент времени . Для случая, когда для всех j, (14) такое же как и полученное в Статье 1, т.е.

 

(17)

 

Результаты расчёта истории добычи выполненные на основе аналитического решения, заданного в (14) и то, что задано численным симулятором, сравниваются на рисунках 2-4. Для случая на Рисунке 2, координаты скважин

Скважины 1 и 2 начинают работу на , скважина 3 начинает на Для случая на Рисунке 3, ,

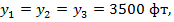
скважина 1 начинает работу на , скважины 2 и 3 на

Рис. 2. Сравнение аналитического и численного решений. Случай одной скважины.

На рисунке 4, , скважины 1 и 2 начинают работу на , скважина 3 начинает на Для всех случаев, кроме тех, которые близки к тем, когда начинается работа скважин, совпадение хорошее.

Рис. 3. Сравнение аналитического и численного решений. Случай двух скважин.

Рис. 4. Сравнение аналитического и численного решений. Случай трёх скважин.

Интересно заметить, что если мы получим полулогарифмический график дебита, мы можем наблюдать экспоненциальное падение общего дебита, , как об этом говорилось в Статье 1. Это показано на рисунках 5 и 6, которые соответствуют рисункам 2 и 4 соответственно. Так же на рисунке 5 видно, что если все скважины работают с одинаковым давлением в стволе, то падение дебита экспоненциально, с тем же показателем, что и общий дебит. Эти наблюдения являются расширением положений, приведенных в Статье 1 и, следовательно, можно использовать методологию анализа производственных данных, предложенная в этой статье, может быть использована для системы со скважинами, начинающими работу в разное время.

Рис. 5. Полулогарифмический график, случай равного давления, одна скважина.

 

Рис. 6. Полулогарифмический график, случай неравного давления, две скважины.

 

Заметим, что показатель снижения изменяется со временем, потому что этот показатель зависит от количества работающих скважин.

Изменения давления в стволе. В приложении С мы представили аналитическое решение, для случая когда перепад давления на каждой скважине может быть изменен со временем. Все скважины начинают работать в одно и то же время. Это решение выражается как

 

 

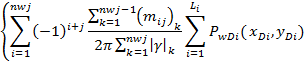
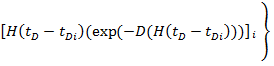
(18)

Где: количество изменений в давлении для i-ой скважины, и

Заметим, что последние члены суммирования в (18) равны:

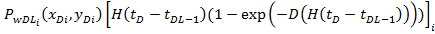
И

 

(18) сводится к (17) когда 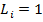для всех i. График на рисунке 7 показывает сравнение аналитического решения, заданного (18) и численного решения для случая, когда , т.е. две скважины симметрично расположены в пласте.

Рис. 7. Сравнение аналитического и численного решений. Изменения в скважинном давлении.

На первой скважине, показанной треугольниками и сплошной линией, изменение происходит на , а на второй скважине, показанной квадратами и пунктирной линией, изменение происходит на 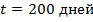. Согласование между двумя решениями очень хорошее.

Рис. 8. Полулогарифмический график с изменениями в скважинном давлении

На рисунке 8 показан полулогарифмический график соответствующий рисунку 7. Мы наблюдаем, что общий дебит экспоненциально уменьшается. Ситуация опять предполагает, что методология анализа, данная в Статье 1 может быть использована, когда давление в стволе скважины изменяется со временем. Заметим, что показатель снижения для не изменяется во времени, потому что не является функцией перепада давления скважин.

 

Изменение состояния скважин. В приложении D представлено аналитическое решение, позволяющее изменять состояние любой скважины в любое время в течении времени работы. Снова предположено, что все скважины начинают работать в одно и то же время с постоянным перепадом давления которое действовало на каждой скважине с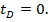

Скважина i имеет изменение в её значении механического скина от до в момент времени . Аналитическое решение для этого случая заданно

 

(19)

Уравнение (19) сводится к (17) когда 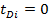для всех i. Рисунок 9 показывает сравнение решений, полученного из (19) и численного результата для случая двух скважин, симметрично расположенных в пласте. Первая скважина была простимулирована в момент времени 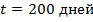, вторая в . Для всех случаев, кроме близких к тем, где происходит изменение состояния любой из двух скважин, согласование между решениями хорошее.

Рис. 9. Сравнение аналитического и численного решений. Изменение состояния скважин.

На рисунке 10 представлен полулогарифмический график, соответствующий рисунку 9.

Рис. 10. Полулогарифмический график с изменением состояния скважин.

Как и ожидалось, основываясь на результатах Рисунков 5,6 и 8, общий дебит снова показывает экспоненциальное падение, подразумевающий, что использование методологии Ссылки 1 может так же быть использовано для случая, когда состояние скважины меняется со временем. Для этого случая показатель снижения, для , это функция времени, потому что она зависит от повреждения скважин.

 

Результаты оптимизации

В этом разделе представлены некоторые результаты, связанные с процедурой оптимизации, которая включает в себя поиск экстремальных значений функции нескольких переменных. Шаблон, используемый в этом исследовании, для оптимизации использует квази-Ньютоновский алгоритм, разработанный для неограниченной минимизации вещественной функции n переменных. В нашем случае переменными являются координаты скважин, уплотняющих проектную сетку разработки, и целевая функция является отрицательной суммой совокупного дебита или отрицательным общим объемом дебита, что эквивалентно максимизации или в определённое время , полученной из интегрирования (4), т.е.

(20)

Или сумме всех безразмерных дебитов скважин

(21)

Следует отметить, что в этой статье и выбрали полную добычу и общий дебит в качестве оптимизируемых функций, но можно было выбрать любую другую функцию в качестве целевой, такую как значение сетки в указанное время.

Отметим, что (14) (и таким образом (20)-(21)) аппроксимировано потому что мы использовали долговременное приближение в его выводе, который подразумевает, что мы проигнорировали наличие ранних переходных процессов, которые возникают, когда скважина начинает работать.

Шаблон, используемый в этом исследовании, основан на методе градиентного спуска, и он использует только значения градиента, а не вторые производные. Производная совокупного дебита по отношению к координатам скважин, уплотняющих проектную сетку разработки, рассчитаны методом конечных разностей, аппроксимируя отрицательную часть целевой функции квадратичным отношением, полученным из ряда Тейлора.

Чтобы ускорить алгоритм оптимизации вместо использования бесконечного ряда, представленного в членах , мы используем сокращенные формы, полученные в приложении B (Уравнение (B-4)).

Рисунок 11 показано использование алгоритма оптимизации для случая, когда скважина начинает работу в нулевое время, а скважина, уплотняющая проектную сетку, начинает работу в момент времени с меньшим перепадом давления, чем на первой скважине. Зависимость и сравнены, они соответствуют линиям с символами и без них, соответственно. Пунктирная линия показывает аналитическое решение с двумя симметрично расположенными скважинами в пласте (). И сплошная линия соответствует случаю, когда и оптимизированы в каждый момент времени. Мы наблюдаем, что влияние процедуры оптимизации меньше, если целевой функцией является , и оно максимизировано, когда целевой функцией является . Фактически, увеличение дебита из-за оптимального положения скважин, является незначительным, этого больше добиваются за счёт ускорения добычи. Так же мы можем наблюдать, что эффект оптимального расположения с обеими целевыми функциями увеличивается со временем.

Рис. 11.Оптимизация суммарного дебита и суммарной добычи. Случай одной скважины.

На рисунке 12 показаны x -координаты, рассчитанные алгоритмом с обеими целевыми функциями, для скважины, уплотняющей проектную сетку.

Рис. 12.Вычисленная безразмерная координата X для обеих целевых функций.

Начальное расположение для обоих случаев было 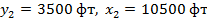. Вычисленная у -координата оставалась постоянной. Мы наблюдаем, что оптимальная позиция второй скважины сдвигалась к правой границе () по мере увеличения времени. Это смещение быстрее когда является целевой функцией, нежели .

Рис. 13.Оптимизация суммарного дебита и суммарной добычи. Случай двух скважин.

Поскольку на практике положение скважины не изменяется, мы можем сделать вывод, основанный на рисунках 11 и 12, что оптимальная позиция скважин будет очень близка к правой границе, чтобы получить максимум и . Этот результат можно было ожидать на основе физических обоснований.

График 13 показывает такой же вид сравнения, как и Рисунок 11 для другого примера. Основной случай, показаный пунктирной линией, соответствует рисунку 3. Сплошная линия, как с символами, так и без, соответствует оптимизированному случаю с обеими величинами и , соответственно. И снова эффект оптимизационной процедуры больше, когда используется в качестве целевой функции, нежели

Рисунок 14 показывает рассчитанные координаты для двух скважин с обеими целевыми функциями и , представленные линиями с символами и без, соответственно. Поскольку обе скважины имеют более высокое давление в стволе, чем исходная скважина, алгоритм выдает х- координату, движущуюся к правой границе. Первоначально, у -координата одинакова для двух скважин, но, когда х- координата приближается, алгоритм производит другие у -координаты.. И снова, как и в предыдущем примере, движение к правой границе быстрее, когда используется в качестве целевой функции, нежели

Рис. 14.Вычисленные безразмерные координаты для обеих целевых функций.

Рисунок 15 показывает случай, когда четыре скважины начинают работать в момент времени с одинаковым давлением в стволе. Начальное расположение, заданное в алгоритме для четырёх скважин:

Целевой функцией является общий совокупный дебит нефти. Заметим, что поскольку все скважины работают с одинаковым перепадом давления, оптимальное положение зафиксировано по времени. В противном случае, оптимальное положение будет функцией времени. Этот результат можно было ожидать, потому что области питания скважин зафиксированы, они зависят только от состояния скважин.

Рис. 15.Рассчётные безразмерные координаты, оптимизирующие совокупную добычу.

Когда скважины работают с одинаковым давлением в стволе, оптимальное расположение, полученное с помощью алгоритма одинаково, независимо от того, является ли суммарный отбор или общий дебит целевой функцией.

Заметим, что если состояние скважины будет известно заранее, то будет возможно узнать оптимальное расположение для бурения скважин в этом случае.

В этом исследовании было найдено, что обе целевые функции, , очень гладкие поверхности с точки зрения скважинных координат. Таким образом, очень часто алгоритм оптимизации находил относительный градиент очень близким к нулю, и предполагалось, что текущая итерация является решением.

Следует упомянуть, что алгоритм оптимизации может гарантировать сходимость локального минимума, но он не гарантирует нахождение глобального. Метод итерационный и находит только приближенные решения задачи. Помимо алгоритма оптимизации, упомянутого выше, другие процедуры оптимизации были применены без успеха. Среди них стоит упомянуть симплекс-метод Нелдера - Мида, а так же метод Пауэлла, основанный на отбрасывании направления наибольшего снижения.

На основании приведенных выше результатов увеличение добычи за счет оптимального расположения скважин, для однородной системы, рассмотренной в данном исследовании, является незначительным. Тем не менее, мы считаем, что наличие разрывов пласта, таких как разломы и линзовидные залежи, изменения условий осадконакопления, анизотропия проницаемости сланцевого прослоя и многофазный поток, сделают процедуру оптимизации более актуальной. Разумеется, использование аналитических целевых функций, как и полученных в этом исследовании, будет невозможно.

 

Заключения

Основываясь на результатах этой работы, обосновываются следующие заключения:

1) Представлены новые выражения для функции Грина на больших временах, присутствующие в аналитических решениях. Эти выражения позволяют уравнению дебита на ранних временах работать лучше, чем предыдущие выражения.

2) Мы продолжили рассматривать аналитическое решение, данное в Статье 1: разное время начала работы скважин, изменения давления в стволе любой скважины в течении их времени работы и изменения состояния любой скважины в любое время.

3) Методология анализа данных добычи, предложенная в Статье 1, может быть использовано для любых из трёх случаев, упомянутых выше. Общий дебит показывает экспоненциальное падение для всех этих случаев, и поведение экспоненциального падения, изложенное в Статье 1, по-прежнему сохраняется для них.

4) Для ускорения алгоритма оптимизации, бесконечные суммы, которые представлены в решении, выражены в сжатой форме.

5) Оптимальное расположение, необходимое для максимизации добычи или общего дебита, является функцией времени, когда скважины работают с разным давлением в стволе. В противном случае, оптимальное положение фиксировано.

6) Влияние оптимизации сильнее, когда целевой функцией является суммарный дебит скважины, а не суммарная добыча. Обе целевые функции дают гладкую поверхность.

Номенклатура

A = площадь пласта, фт² [м²]

B = объёмный коэффициент

Ct = общая сжимаемость, psi^-1 [кПа]^-1

D = коэффициент падения

h = толщина пласта, фт [м]

k = абсолютная проницаемость, Дарси [м²]

nw = число скважин

= давление, psi [кПа]

= безразмерное давление в пространстве Лапласа

= начальное давление, psi [кПа]

= безразмерное забойное давление скважины j

= текущее забойное давление скважины j, psi [кПа]

= рабочее давление на забое скважины, psi [кПа]

= общий дебит пласта, баррель/день [м³/день]

= безразмерный дебит пласта

= дебит скважины j, баррель/день [м³/день]

 

= безразмерный дебит скважины

= безразмерный дебит скважины j в пространстве Лапласа

= радиус ствола скважины

s = параметр пространства Лапласа

S = коэффициент повреждения скважины

t = время, часы, дни

= безразмерное время основанное на А

x,y = пространственные координаты фт [м]

= длина пласта по x, фт [м]

= безразмерная длина пласта по x

= длина пласта по y, фт [м]

= безразмерная длина пласта по y

= вязкость жидкости сП [Па.с]

= пористость

Нижние индексы

D = безразмерный

e = внешний

s = свойство скин-зоны

w = относящийся к стволу скважины

 

Ссылки

1. Rodriguez, F. and Cinco-Ley, R: "A New Model for Production Decline," Paper SPE 25480, presented at the Production Operations Symposium, Oklahoma, OK, March 21-23, 1993.

2. Hurst, W.: “Unsteady Flow of Fluids in Oil Reservoirs," Physics (Jan. 1934) 5, 20.

3. van Everdingen, A.F. and Hurst, W.: “The Application of the Laplace Transformation to Flow Problems in Reservoirs," Trans. AIME( 1949) 186,305-324.

4. Jacob, C.E. and Lohman, S.W.: “Nonsteady Flow to a Well of Constant Drawdown in an Extensive Aquifer”, Trans.. AGU (Aug. 1952) 559-569.

5. Uraiet, AA and Raghavan, R: "Unsteady Flow to a Well Producing at a Constant Pressure," JPT (Oct. 1980), 1803­-1812.

6. Ehligh-Economides, C.A and Ramey, HJ., Jr.: ‘Transient Rate Decline Analysis for Wells Produced at Constant Pressure," SPEJ (Feb. 1981)98-104.

7. Camacho-V., R. G.:" Constant Pressure Production in Solution Gas-Drive Reservoirs: Transient Flow, " SPEFE (June 1991), 199-208.

8. Jones, J. R. and Raghavan, R: “Interpretation of Flowing Well Response in Gas Condensate Wells, " SPEFE (Sept. 1988) 578-594.

9. Camacho-V., R G. and Raghavan, R: " Boundary- Dominated Flow in Solution-Gas-Drive Reservoirs, " SPERE, (Nov. 1989), 503-12.

10. Fraim, M. L. and Wattenbarger, R A: “Decline Curve Analysis for Multiphase Flow," Paper SPE 18274 presented at the 63rd Annual Technical Conference and Exhibition of the Society of Petroleum Engineers held in Houston, TX. Oct. 2-5, 1988.

11. Camacho-V., R G. and Raghavan, R: “Some Theoretical Results Useful in Analyzing Well Performance Under Solution-Gas Drive," SPEFE, (Jun. 1991), 190-198.

12. Chen, H Y. and Poston, S. W.:" Application of a Pseudotime Function to Permit Better Decline-Curve Analysis, " SPEFE (Sept. 1989) 421-28.

13. Vo, D.T. and Raghavan, R: "An Approximate Analysis Method for Multiphase Flow Data," SPEFE (March, 1991), 121-28.

14. Camacho-V., R G., Vasquez-C., M.A, and Padilla-S., R: "New Results on Decline Curves Considering Non-Darcy Flow Effects," Paper SPE 24058 presented at Western Regional Meeting held in Bakersfield, CA March 30-April 1, 1992.

15. Fraim, M. L. and Wattenbarger, R A: “Gas Reservoir Decline-Curve Analysis Using Type Curves With Real Gas Pseudopressure and Normalized Time," SPEFE (Dec., 1987), 671-682.

16. Schmid, S.H, Caudle, B.H, and Miller, M.A: “Gas Well Decline Analysis Incorporating Rea] Gas Behavior and Non-

Darcy Flow," Paper SPE 15521, presented at 61st SPE Annual Technical Conference, New Orleans, LA

17. Harrington, A G. et. al.: “Application of Type-Curve Techniques to Decline Analysis and Forecasting of Gas Wells, " Paper SPE 16936 presented at the 62nd Annual Technical Conference and Exhibition of the SPE held in Dallas TX, Sept. 27-30, 1987.

18. Berumen, C.S., Samaniego, F., and Cinco-Ley, H: "Transient Pressure Analysis and Performance of Gas Wells Producing Under Constant Pressure Conditions," Paper SPE 19098 presented at the 1989 SPE Gas Technology Symposium, Dallas TX, June 7-9.

19. Aminian, K., Ameri, S., Puon, P.S., and Rieke, RR: "Production History Analysis in Predicting Dry Gas-Well Performance," Journal of Petroleum Science and Engineering, 2 (1989) 13-26. Elsevier Science Publishers B.V., Amsterdam.

20. Fraim, M.L. and Lee, W.J.: “Determination of Formation Properties From Long-Term Gas Well Production Affected By Non-Darcy Flow,” Paper SPE 16934 presented at the 62th Annual Technical Conference and Exhibition of the SPE, Dallas TX, 1987.

21. Arps, J.J.: “Analysis of Decline Curves," Trans.. AIME (1945) 160, 228-247.

22. Fetkovich, M. J.: “Decline Curve Analysis Using Type Curves, " JPT (June 1980) 1065-1077.

23. Mavor, M.J. and Cinco-Ley, H.: "Transient Pressure Behavior of Naturally Fractured Reservoirs," Paper SPE 7977 presented at the California Regional Meeting, Ventura, April 18-20, 1979.

24. Raghavan, R and Ohaeri, C.U.: "Unsteady Flow to a Well Produced at Constant Pressure in a Fractured Reservoir," Paper SPE 9902 presented at the California Regional Meeting, Bakersfield, March 25-26, 1981.

25. Da Prat, G., Cinco-Ley, R, and Ramey, RJ. Jr.: "Decline Curve Analysis Using Type Curves for Two-Porosity System," SPEJ (June 1981), 354-362.

26. Ozkan, E, Ohaeri, C.U., and Raghavan, R: "Unsteady Flow to a Well Produced at Constant Pressure in a Fractured Reservoir," SPEFE (June 1987), 186-200.

27. Sageev, A, Da Prat, G., and Ramey, RJ., Jr.: "Decline Curve Analysis for Double-Porosity Systems," Paper SPE 13630 presented at the California Regional Meeting, Bakersfield, March 27-29, 1985.

28. Olarewaju, J.S. and Lee, W.J.: "Rate Behavior of Composite Dual-Porosity Reservoirs," Paper SPE 21703 presented at the Production Operation Symposium, Oklahoma City, OK, April 7-9,1991.

29. Guppy, K. R, Cinco-L., R, and Ramey, R J.Jr.: "Effect of Non-Darcy Flow on the Constant-Pressure Production of Fractured Wells," SPEJ (June 1981).

30. Resurreiсao, C.E and Rodriguez, F.: “Production Decline Analysis of Finite-Conductivity Fractured Wells," SPE 23704 presented at IILAPEC, Caracas, Ven., 8-11 March 1992.

31. Russell, D.G. and Prats, M.: "Performance of Layered Reservoirs with Crossflow - Single-Compressible-Fluid Case," SPEJ, (March, 1962).

Katz, M.L. and Tek, M.R: "A Theoretical Study of Pressure Distribution and Fluid Flux in Bounded Stratified Porous Systems with Crossflow," SPEJ, (March, 1962).

32. Olarewaju, S.A and Lee, W.J.: "The Rate Performance of a Layered Reservoir with Unsteady-State Interlayer Crossflow," Paper SPE 18544 presented at the Eastern Regional Meeting, Charleston, WV, November, 1988.

33. Zhang, W.G., Chu, L., and Grader, AS.: "Rate Decline of an Arbitrarily Positioned Well in Composite and Irregular Reservoirs," Paper SPE 26913 presented at the Eastern Regional Conference a