Тема 2.1.3.1 Средняя арифметическая величина и ее средняя квадратическая погрешность.
Арифметическое среднее
Если имеется ряд результатов равноточных измерений l1; l2; …; ln одной и той же величины, то за окончательное значение принимают среднюю арифметическую величину X из всех результатов.
Xср =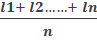 
= 
Если неизвестно истинное (точное) значение измеряемой величины, что обычно и бывает на практике, то возникает вопрос, какую же величину принимать за вероятнейшее значение?
Для ответа на этот вопрос запишем результаты ряда равноточных измерений в виде. Если истинное значение измеряемой величины х, то абсолютные ошибки (∆) будут равны:
Δ 1= l1- X;
Δ 2= l2- X;
Δ n= ln- X,
Сложив левые и правые части этих равенств получим
[ Δ ] = [ l ] – nX.
Разделив обе части этого равенства на п, будем иметь
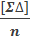= Xср-X
где
Хср - X = η| — истинная погрешность арифметического среднего.
По третьему свойству случайных ошибок (среднее арифметическое ряда ошибок равноточных измерений при неограниченном возрастании числа измерений стремится к нулю), т. е.
= 
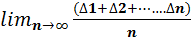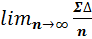=0
поэтому при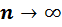 
Хср 
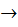Xист.
Следовательно, при неограниченно большом числе измерений и отсутствии систематической ошибки, арифметическое среднее стремится к истинному значению измеряемой величины. По этой причине его называют вероятнейшим значением измеряемой величины. В практике число измерений естественно ограничено, поэтому арифметическое среднее может заметно отличаться от истинного значения.
Средняя квадратическая ошибка(погрешность) измерений
Для оценки точности измерений, т. е. для определения степени близости результата измерения к истинному значению измеряемой величины, чаще всего определяют среднюю квадратическая ошибку. Точность измерений характеризуется СКП измерения по формуле, предложенной Гауссом:
|
|
m =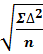 
Величина т (точность измерений) является также случайной величиной, зависит от числа измерений и сама определяется с ошибкой:
mm=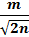 
Для определения допустимости полученной ошибки вычисляют предельную ошибку ∆пр, больше которой ошибки относятся уже к грубым.
Величину предельной ошибки определяют по формуле
∆пр=km 
где k = 2 (вероятность 0,95) или 3 (вероятность 0,997)
Точность геодезических измерений характеризуется абсолютными и относительными ошибками.
Абсолютными являются истинные, средние квадратические и предельные.
Относительной ошибкой ε называется отношение соответствующей абсолютной ошибки к истинному измеряемой величины. Ее выражают в виде дроби, где в числителе единица.
Если измеренную величину обозначить Хср, то относительная СКО (ε m( эпсилон))
ε m = 
= 
;
ε пр =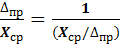 
где ε m и ε пр - соответственно относительная средняя квадратическая и предельная ошибки.
Вычисление среднеквадратической ошибки по формуле Гаусса возможно только тогда, когда известны истинные ошибки измерений, однако в большинстве случаев они не известны. Поэтому на практике задача решается через уклонения результатов измерений от их арифметического среднего v (вероятнейшие ошибки), которые вычисляются по результатам многократных измерений.
В этом случае среднеквадратическая ошибка вычисляется по формуле Бесселя
|
|
m =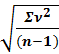 
где v — вероятнейшие ошибки: v = Хi - Хср
Среднюю квадратическую ошибку арифметической середины М выражают через СКО отдельного измерения(m), т. е
M=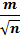 
Таким образом, средняя квадратическая ошибка арифметической середины из результатов равноточных измерений в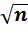 
раз меньше средней квадратической ошибки результата отдельного измерения. Для уменьшения ошибки измерения, например, в 2 раза, количество измерений необходимо увеличить в 4 раза.