КОНСТРУИРОВАНИЕ ПРОГРАММ ЦИКЛИЧЕСКОЙ СТРУКТУРЫ

С ПОСТУСЛОВИЕМ

Цель работы

 

Изучение использования оператора типа DO-WHILE в программировании циклических процессов.

 

Методические указания

 

Оператор типа DO используется в тех случаях, когда тело цикла должно выполняться хотя бы один раз.

Формат оператора do:

 

do

оператор;

while (выражение);

Схема выполнения оператора DO:

1)выполняется оператор;

2)вычисляется выражение. Если оно не равно нулю (истинно), то выполнение продолжается с шага 1. Если он принимает значение, равное нулю, то работа оператора DO заканчивается. Управление передается следующему за ним оператору программы.

Для прекращения работы оператора до того, как условие, представленное выражением, станет ложным, используется оператор break. Это оператор должен работать, когда выполняется условие, по которому необходимо прервать работу цикла. Этому случаю должен соответствовать условный оператор, стоящий внутри тела цикла, а именно:

 

if (условие_досрочного_прекращения)

break;

В отличие от оператора while, проверяющего условие в начале цикла, оператор do-while проверяет условие в конце цикла.

Пример:

x = 1;

do

printf (²%d \n², power (x, 2));

while (++x <=7);

В данном примере в роли параметра цикла (управляющей переменной) выступает переменная x, которой присваивается начальное значение x = 1, а затем она в каждом цикле увеличивается на единицу.

Операторы цикла используются при вычислении различных сумм и произведений. При этом часто целесообразно использовать некоторые преобразования, позволяющие избежать трудностей, связанных с вычислением степеней и факториалов.

При вычислении сумм членов ряда вида

член суммы может относиться к одному из следующих трех типов.

Он может иметь вид:

В первом случае целесообразно использовать рекуррентное соотношение, выражающее следующий член ряда через предыдущий, что позволяет избежать прямого вычисления факториала n!.

Пусть нужно вычислить сумму

Здесь . Воспользовавшись рекуррентным соотношением для n! = (n - 1)!n, найдем равенство, связывающее c для любого n, для чего рассмотрим отношение к .

, отсюда следует соотношение, связывающее два соседних члена ряда

n + 1 = ×J.

Программа вычисления суммы в этом случае будет иметь вид:

main ()

{ int n = 1;

float S, x;

S = 0; a = x;

scanf (² %e ², &x);

do

{ S = S + a;

n ++;

a = a*(-x*x/((2*n+2)*(2*n+3)));

}

while n < 100;

printf (²Сумма равна %e \n², S)

}

Во втором случае применение рекуррентных соотношений нецелесообразно, так как общий член ряда может быть вычислен непосредственно по формуле.

В третьем случае член суммы можно представить в виде двух сомножителей, один из которых вычисляется по рекуррентному соотношению, а другой - непосредственно.

Пример выполнения задания

Составить программу вычисления значения некоторой функции y = f(x) по рекуррентным выражениям вида:

Текст программы будет иметь вид:

main ()

{ int k;

float x, z, U;

scanf (² %d ², &x);

y = U = z = (x-1)/(x+1);

k = 1;

do

{U = U*z*z(2*k-1)/(2*k+1);

y = y - U;

}

while k++ < 100;

printf (²Значение функции y = %d \n², y)

}

Следует отметить, что в математической постановке задачи означают соответственно новое значение U и y, и прежнее значение этих переменных.

 

Контрольные вопросы

Приведите синтаксическую структуру оператора DO-WHILE.

Чем отличается эта форма оператора цикла от ранее рассмотренных?

Как досрочно прервать выполнение циклического оператора DO-WHILE?

Что является телом в этом операторе цикла?

Когда выполняется проверка условия в этом цикле?

Что может использоваться в качестве условия? Приведите примеры.

 

Варианты заданий

1.Найти n, при котором отличается от функции sh(x) на величину 0.0001. Функция гиперболический синус имеет вид: .

2. Найти n, при котором отличается от функции сh(x) на величину 0.001. Функция гиперболический косинус имеет вид: .

3. Вычислить значение функции th(x) по формуле при n = 100 и найти абсолютную погрешность вычисления th(x), если , а

4. Вычислить значение функции по формуле при N = 100. Вывести на экран абсолютную погрешность вычисления.

5. Вычислить сумму для n = 40, x = p/2 и подсчитать абсолютную погрешность

6. Функция представляется суммой . Вычислить приближенное значение этой функции для x = 0.2, n = 20 и оценить абсолютную погрешность вычисления.

7. Функция представляется суммой . Вычислить значение этой функции для x = 0.5, n = 30 и оценить абсолютную погрешность вычисления.

8. Функция представляется суммой
. Вычислить ее значение при x = p/5 и n = 40 и оценить абсолютную погрешность вычисления.

9. Вычислить значение и определить, будет ли вычисление функции sh(x) по данной формуле точнее, чем вычисление по формуле, приведенной в п.1.

10. Вычислить значение и определить, будет ли вычисление функции ch(x) по данной формуле точнее, чем вычисление по формуле, приведенной в п.2.

11. Функция может быть вычислена по формуле . Определить, при каком N совпадают значения функции, вычисленные по первой и второй формулам.

12. Найти значения функции y = sh(x), используя рекуррентные соотношения

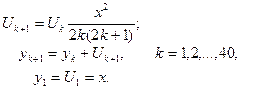
13. Найти значение функции y = ch(x), используя рекуррентные соотношения

14. Найти абсолютную погрешность вычисления функции y = sin(x) по приближенной формуле .

15. Значение функции y = ln(x) может быть вычислено по рекуррентным выражениям вида:

Значение x £ 0 вводится с клавиатуры. Найти абсолютную погрешность вычисления y = ln(x) по рекуррентным соотношениям и непосредственно путем обращения к стандартной функции lnx.

16. Функция представляется приближенно формулой . Вычислить ее значение по первой и второй формулам, взяв x = 0.2, n = 100, и определить абсолютную погрешность вычисления.

17. Функция y = sin(x) может быть вычислена с помощью рекуррентных соотношений

Реализовать программу вычислений y = sin(x), используя рекуррентные соотношения. Определить абсолютную погрешность вычисления при k = 100.

18. Вычислить точное значение функции , приближенное, используя представление в виде суммы и абсолютную погрешность.

19. Функция y = arcsin(x) может быть представлена в виде суммы 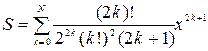при |x| < 1. Вычислить точное, приближенное значение и абсолютную погрешность вычисления по первой и второй формулам.

20. Функция y = arctg(x) приближенно представляется суммой вида: при |x| < 1. Вычислить значение функции по этой формуле и оценить абсолютную погрешность.

21. Функция arcsec(x) представляется суммой для |x| > 1. Вычислить, насколько отличаются друг от друга значения функции, вычисленные при

22. Вычислить значения гамма-функции Г(x) по приближенной формуле , где g = 0.57722, для двух значений и оценить, насколько изменилось значение функции при N₂ = 200 по сравнению со значением при N₁ = 100.

23. Вычислить значение интегрального косинуса Ci(x) при x > 2 при двух значениях N = 50 и N = 100, если приближенно эта функция вычисляется по формуле .

24. Вычислить значение интегрального синуса Si(x) по формуле при x £ 2 для двух значений N = 50 и N = 100 и вывести на экран разность результатов этих двух вычислений.

25. Вычислить значение интегрального косинуса Ci(x) по формуле 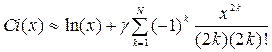, где x £ 2, g = 0.57722, для N = 50 и N = 100 и оценить разность этих двух вычислений.

 

 

Лабораторная работа № 7