Тема 1. Системы линейных уравнений
Система уравнений называется линейной, если все уравнения, входящие в систему, являются уравнениями первой степени относительно переменных. Если система из n линейных уравнений содержит n неизвестных, то возможны следующие три случая:
1) система не имеет решений;
2) система имеет единственное решение;
3) система имеет бесконечно много решений.
Рассмотрим решение систем линейных уравнений с помощью определителей.
1. Система двух линейных уравнений с двумя неизвестными
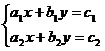. (1)
имеет единственное решение, которое вычисляется по формулам Крамера:
, 
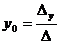
при условии, что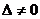 
. Числа 
, 
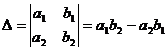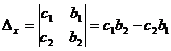и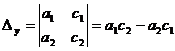 
называются определителями второго порядка.
Пример. Решите с помощью определителей систему 
.
Решение. Вычисляем определители: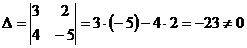 
;
; 
.
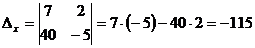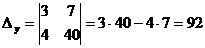Тогда по формулам Крамера получаем:
; 
.
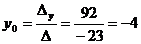Ответ: (5;-4).
СВОЙСТВА ОПРЕДЕЛИТЕЛЕЙ
Рассмотрим свойства определителей на примере определителей второго порядка:
.
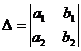Числа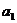 
, 
, 
, 
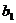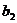называются элементами определителя. Определитель второго порядка равен разности между произведением его элементов, стоящих на главной диагонали (идущей слева направо вниз) и произведением элементов, стоящих на второй диагонали.
Свойства определителей
1. Величина определителя не изменится от замены строк столбцами:
.
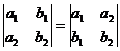2. Величина определителя от перестановки любых двух параллельных его рядов меняет знак на противоположный:
; 
.
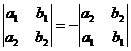3. Определитель равен нулю, если оба элемента какой-либо строки или столбца равны нулю:
; 
.
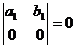4. Определитель равен нулю, если в нём пропорциональны (или равны) соответствующие элементы его строк или столбцов:
; 
; 
; 
.
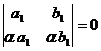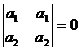Пример:
; 
.
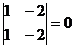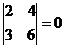5. Чтобы умножить определитель на произвольный множитель, достаточно на него умножить элементы одной какой-либо строки или одного какого-либо столбца определителя:
.
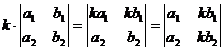Таким образом, общий множитель элементов одного ряда можно выносить за знак определителя.
Пример:
.
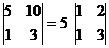6. Величина определителя не изменится, если к элементам одного ряда прибавить элементы параллельного ряда, умноженные на одно и то же число:
.
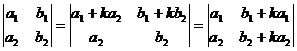2. Рассмотрим систему трёх линейных уравнений с тремя неизвестными:
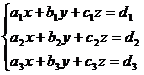(2)
при условии, что определитель системы
.
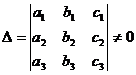В этом случае система (2) имеет единственное решение, которое вычисляется по формулам Крамера:
; ; 
,
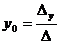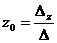где
; 
; 
.
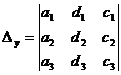Определитель третьего порядка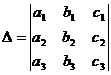 
можно вычислять по формуле, которая называется формулой разложения определителя третьего порядка по элементам первой строки:
.
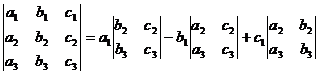Пример: Вычислить определитель 
.
.
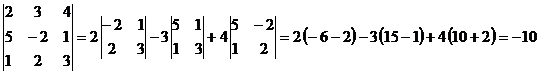Свойства 1-6 определителей второго порядка распространяются также на определители третьего порядка.
Пример. Решите систему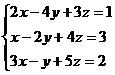 
.
Решение. Вычисляем определители:
;
;
;
.
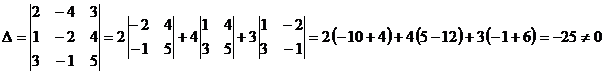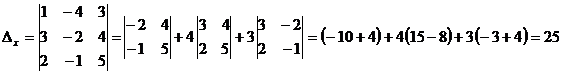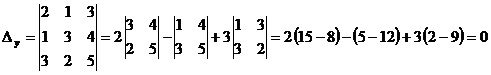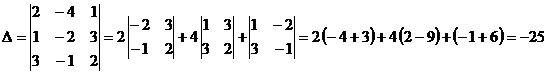По формулам Крамера получаем:
; 
; 
.
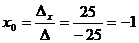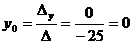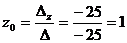Ответ: (-1;0;1).
Если в системе (2) определитель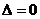 
, то возможны следующие случаи:
I. Элементы двух строк определителя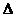 
пропорциональны, например,
.
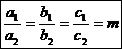Тогда: 1) если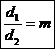 
, то система неопределённа;
2) если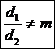 
, то система несовместна.
Пример: Решите систему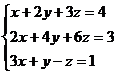 
.
Определитель системы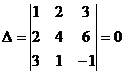 
, при этом элементы двух строк определителя пропорциональны: 
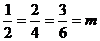, но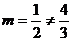 
. Тогда данная система несовместна.
II. В определителе 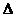нет строк с пропорциональными элементами. Тогда существуют отличные от нуля числа m и n, такие, что
.
1) если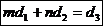 
, то система неопределённа;
2) если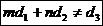 
, то система несовместна.
В заключение рассмотрим решение системы трёх линейных однородных уравнений с тремя неизвестными:
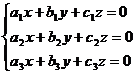. (3)
Система (3) имеет отличные от нуля решения тогда и только тогда, когда определитель системы
.
Пример: Решите систему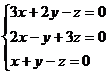 
.
Вычисляем определитель системы:
.
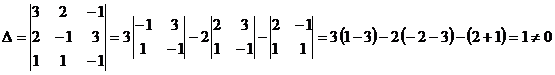Следовательно, система имеет единственное решение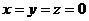 
.
Тема 2. Матрицы и действия над ними. Основные определения
Определение 1. Матрицей называется таблица чисел aik вида: 
состоящая из m строк и n столбцов. Числа aik называются её элементами. Это прямоугольная матрица. В частности, если m =1, n >1, получаем матрицу-строку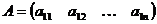 
, а если m >1, n =1, матрицу-столбец: 
.
Определение 2. Матрица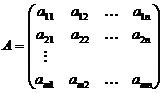 
называется невырожденной (неособой), если её определитель 
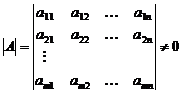и вырожденной (особой), если 
.
Определение 3. Матрица называется квадратной, если m=n (n – порядок матрицы). В частности, матрица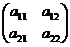 
называется квадратной матрицей второго порядка, а матрица 
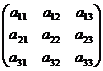- квадратной матрицей третьего порядка.
Определение 4. Квадратная матрица называется диагональной, если все элементы, стоящие вне главной диагонали равны нулю: aij =0 i¹j.
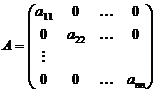
В частности, диагональная матрица, у которой все диагональные элементы равны единице называется единичной.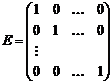 
Определение 5. Нулевой матрицей называется матрица, все элементы которой равны нулю:
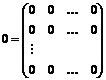
Действия над матрицами
Определение 1. Две матрицы A и B называются равными, если они одинакового размера (т.е. имеют одинаковое число строк и одинаковое число столбцов) и их соответствующие элементы равны. В частности, есл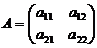и
и 
и A = B, то a 11= b 11, a 12= b 12, a 21= b 21, a 22= b 22.
Матрицы одинакового размера можно складывать и вычитать.
Определение 2. Суммой двух матриц A и B называется матрица С, элементы которой равны сумме соответствующих элементов матриц A и B (обозначение C=A+B). В частности, для квадратных матриц второго порядка получаем:
, 
, 
.
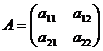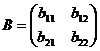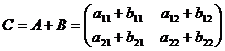Пример. Найдите сумму матриц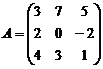 
и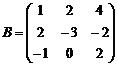 
.
Сумма нулевой матрицы и любой матрицы A даёт матрицу A: A +0 = A.
Определение 3. Разностью двух матриц A и B называется матрица С, элементы которой равны разности соответствующих элементов матриц A и B (обозначение C=A+B).
Пример. Найдите разность матриц 
и 
.
.
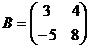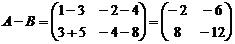Определение 4. Произведение матрицы A на число a называется матрица, элементы которой получаются из соответствующих элементов матрицы А умножением на число a.
Пример. Найдите матрицу 3 A +5 B, если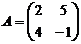 
, 
.
, 
, 
.
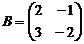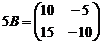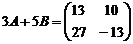Определение 5. Произведение матриц А × В определено в том и только в том случае, если число столбцов матрицы А равно числу строк матрицы В. Произведение матрицы А размера m´k на матрицу B размера k´n называется матрица C=A×B размера m´n, элементы которой определяются по формуле: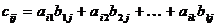 
Данная сумма представляет собой сумму произведений соответствующих элементов строки i матрицы А и столбца j матрицы В.
Рассмотрим правило умножения квадратных матриц второго порядка. Пусть даны две матрицы: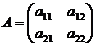 
и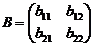 
.
Произведением матрицы A на матрицу B называется матрица C = AB, равная:
.
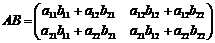Пример. Найдите произведение A·B и B·A матриц 
и 
.
Пример.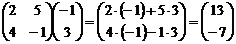 
По отношению к произведению двух матриц переместительный закон не выполняется, т.е. A·B ≠ B·A.
Произведение единичной матрицы и любой матрицы A даёт матрицу A: EA = AE=A.
Определение 6. Матрица AT полученная из матрицы А заменой строк столбцами, называется транспонированной.
Пример. ,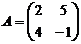 
.
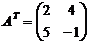Обратная матрица
Определение 1. Пусть A – квадратная матрица n –го порядка, а E – единичная матрица того же порядка. Матрица A–1 называется обратной по отношению к матрице A, если выполняются равенства: A×A–1= A–1×A=E.
Определение 2. Минором какого-либо элемента определителя называется определитель, полученный из данного вычёркиванием той строки и того столбца, которым принадлежит этот элемент.
Минор элемента aik определителя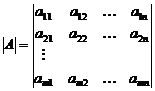 
обозначается Mik.
Пример. Минор M 12 определителя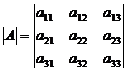 
равен 
.
Определение 3. Алгебраическим дополнением Aik элемента aik определителя 
называется его минор Mik, взятый со знаком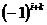 
. Следовательно, 
.
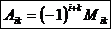Пример. Алгебраическое дополнение A 12 определителя 
равно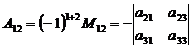 
.
Теорема. Матрица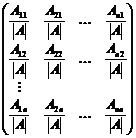 
,
где Aik – алгебраическое дополнение элемента aik невырожденной матрицы A, является обратной для A.
Для матрицы 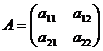обратной является матрица 
.
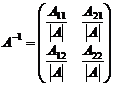Пример. Дана матрица 
. Найдите обратную матрицу.
, 
, 
, 
, 
.
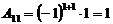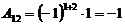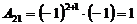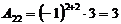Тогда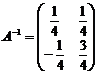 
. Сделаем проверку: 
.