Момент светового давления

Возмущающие моменты

1. Обзор возмущающих моментов

2. Гравитационный момент

3. Аэродинамический момент

4. Момент светового давления

5. Момент магнитной природы

Обзор возмущающих моментов

Внешний возмущающий момент , действующий на космический аппарат, в общем случае складывается из четырех основных составляющих: гравитационного момента , аэродинамического момента , момента светового давления 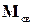, а также момента магнитной природы – то есть

(1)

Помимо названных на космический аппарат могут действовать и другие возмущающие моменты – связанные с ударами микрометеоритов и т.п., однако все они пренебрежимо малы. Особо выделяют постоянный в связанной системе координат реактивный момент, вызванный негерметичностью конструкции космического аппарата, а также момент прерывистого характера, возникающий вследствие отброса некоторых масс (например, в системе жизнедеятельности).

Если произвести численное сравнение моментов, входящих в формулу (1), то в зависимости от конкретных условий каждый из них может быть основным в указанной сумме.

Так, при полетах вдали от планет, когда достаточно учитывать взаимодействие космического аппарата только с Солнцем (на расстоянии порядка 1 а. е.), основной вклад дает .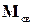

При полетах вблизи Земли преобладает до высот 200-300 км, – с высот около 400 км, 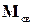– при удалении от Земли на несколько ее радиусов, а может иметь тот же порядок, что и , и даже больше, но это в значительной степени зависит от электротехнических данных.

Если же полет совершается в окрестности других небесных тел, то приведенные выше оценки высот, соответствующие околоземному полету, могут резко измениться. Вблизи Луны и практически равны нулю и основной вклад дают и, возможно, 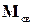. Вблизи Марса атмосфера более разрежена, а масса меньше земной, поэтому высота, где сравниваются и , изменится по сравнению с аналогичным значением для полетов у Земли.

Стоит отметить, что данные сравнительные оценки возмущающих моментов весьма условны, поскольку имеет место их зависимость от массы, формы, траектории полета космического аппарата и т. п. Так, для аппарата, имеющего эллипсоид инерции сферической формы (главные моменты инерции равны), 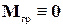, а идеальная центровка или специально выбранный режим ориентации могут дать 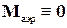и т. д.

Гравитационный момент

Рассмотрим движение космического аппарата в поле тяготения некоторого небесного тела (планеты) с гравитационной постоянной .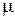

Гравитационный момент , действующий на космический аппарат относительно его центра масс, возникает вследствие того, что центр масс и центр тяжести аппарата в общем случае не совпадают. Действительно, векторы ускорения силы тяжести в различных точках космического аппарата всегда различны, поскольку все они направлены к центру притяжения планеты, а следовательно, если рассматриваемые точки не лежат на одной прямой, идущей через центр притяжения, то векторы не параллельны, а если точки лежат на одной такой прямой, то имеют различное удаление от центра притяжения и, значит, соответствующие ускорения отличаются по величине.

Гравитационный момент для космического аппарата с тензором инерции 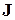в выбранной системе координат рассчитывается по формуле [?]

,

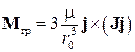(2)

где 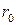– расстояние от центра масс космического аппарата до центра притяжения планеты, а 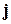– орт местной вертикали.

В орбитальной системе орт 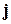имеет координаты 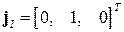. При переходе к связанной системе координат используются элементы 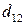, и второго столбца матрицы направляющих косинусов : .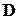

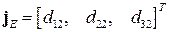В частном случае, когда космический аппарат движется по круговой орбите с угловой скоростью , а оси связанной системы координат совпадают с его главными осями инерции, формула (2) упрощается и приобретает вид

.

(3)

Аэродинамический момент

Взаимодействие корпуса космического аппарата с атмосферой планеты вызывает появление аэродинамических сил и моментов. Плотность атмосферы убывает по мере удаления от поверхности планеты. Для Земли закон изменения плотности атмосферы 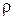от высоты 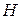над уровнем моря согласно ГОСТ Р25645.166–2004 описывается формулой

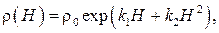
(4)

где 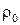– стандартная плотность атмосферы на уровне моря, 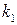и 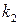– параметры модели атмосферы. Таким образом, при движении космического аппарата на больших высотах целесообразно рассматривать модель взаимодействия корпуса аппарата с отдельными молекулами разреженной среды, а при движении в плотных слоях атмосферы – модель обтекания корпуса сплошной средой.

Соударения молекул разреженной среды с корпусом космического аппарата могут быть упругими или неупругими. Практика показывает, что преобладают неупругие соударения. Согласно закону сохранения импульса элементарная сила, действующая на площадку 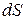, рассчитывается из соотношения

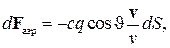
(5)

где 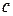– аэродинамический коэффициент, – скоростной напор, – угол между внешней нормалью к элементарной площадке 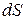и вектором скорости 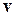этой площадки относительно внешней среды. Для неупругих соударений . Полная аэродинамическая сила , действующая на космический аппарат, и полный аэродинамический момент относительно его центра масс соответственно равны

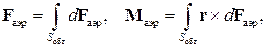
(6)

где 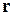– радиус-вектор площадки 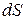с началом в центре масс космического аппарата, 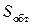– часть поверхности аппарата, обтекаемая внешней средой. Входящая в (5), а следовательно, и в (6) скорость 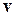складывается из скорости центра масс и линейных скоростей элементарных площадок внешней поверхности корпуса космического аппарата, связанных с его вращением. Это позволяет представить полный аэродинамический момент в виде суммы

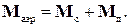
(7)

Аэродинамический момент стационарный , связанный с линейной скоростью центра масс, является функцией конфигурации внешней поверхности аппарата и положения его корпуса относительно вектора . Аэродинамический момент демпфирующий 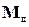, обусловленный вращением вокруг центра масс, будет, кроме того, являться функцией угловой скорости космического аппарата. В задачах активной ориентации обычно полагают, что 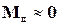, а 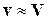. Это позволяет считать, что в условиях разреженной атмосферы элементарные аэродинамические силы представляют собой систему параллельных сил, с равнодействующей , направленной противоположно вектору .

Положение корпуса космического аппарата относительно вектора скорости его центра масс в соответствии с ГОСТ 20058-80 определяется двумя углами: углом атаки 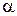и углом скольжения (рис. 1), реже пространственным углом атаки и аэродинамическим углом крена .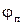

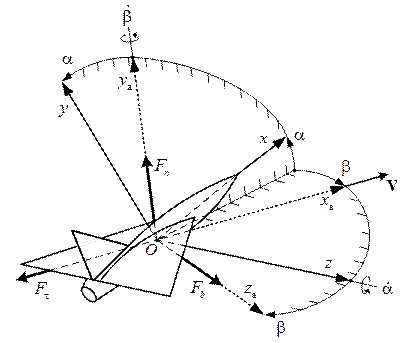
Рис. 1. Скоростная система координат, аэродинамические углы

Для того чтобы рассчитать аэродинамические воздействия при обтекании космического аппарата сплошной воздушной средой, необходимо создать макет (уменьшенную копию) данного аппарата либо разработать его компьютерную модель. Первый способ является более точным, но требует значительных затрат на проведение испытаний опытного образца в аэродинамической трубе. Второй способ требует разработки сложного программного обеспечения, но при этом позволяет вносить корректировки в модель объекта и среды без необходимости повторного макетирования или изменения условий эксперимента. Полную аэродинамическую силу обычно рассматривают в виде ее составляющих по соответствующим осям скоростной системы координат (ГОСТ 20058-80): сила лобового сопротивления , подъемная сила и боковая сила 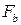(рис. 1), – каждая из которых определяется в виде

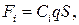
(8)

где – аэродинамический коэффициент силы 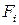, 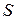– характерная площадь (миделево сечение) космического аппарата. Аэродинамический момент сначала рассчитывается относительно некоторого условного положения центра масс аппарата в проекциях на оси связанной системы координат. Каждая из проекций вектора вычисляется по формуле

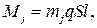
(9)

где – аэродинамический коэффициент момента , – характерная длина космического аппарата (обычно по продольной оси). Затем определяется момент относительно реального положения центра масс:

(10)

Здесь – вектор, соединяющий условное и реальное положения центра масс. Коэффициенты и определяются как функции от аэродинамических углов по результатам испытаний или на компьютерной модели.

Момент светового давления

Световое давление, связанное с излучением некоторого мощного источника света, может породить силы и моменты, действующие на корпус космического аппарата, пренебрежение которыми недопустимо. Такими источниками света при полете космического аппарата в пределах Солнечной системы могут быть Солнце и планеты. В частности, иногда учитывается излучение Земли. Здесь рассмотрим лишь солнечное излучение, принимая Солнце за точечный источник света. Пучок солнечных лучей вследствие малости космического аппарата по сравнению с расстоянием до Солнца будем считать параллельным.

Поток световой энергии изменяется обратно пропорционально квадрату расстояния 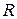от точечного источника света:

.

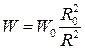(11)

Здесь – поток световой энергии вблизи орбиты Земли, то есть на расстоянии от Солнца. Величина светового давления равна отношению потока световой энергии к скорости света 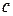, то есть

,

(12)

где 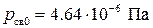– световое давление на расстоянии 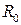от Солнца.

При падении света на различные элементы поверхности космического аппарата в общем случае могут наблюдаться эффекты отражения, поглощения, пропускания и рассеяния. Соответствующие коэффициенты в сумме дают единицу: 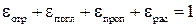. Эффектами пропускания и рассеяния света обычно пренебрегают (исключением является, например, наличие антенн сетчатой конструкции), поэтому будем рассматривать только силы и моменты, возникающие в результате отражения света от корпуса космического аппарата и поглощения света корпусом. Пусть задан коэффициент отражения материала корпуса 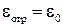, тогда коэффициент поглощения будет равен .

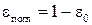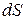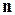Рассмотрим солнечный свет как поток фотонов, падающий в направлении в течение времени на элементарный участок поверхности космического аппарата площадью под углом к внешней нормали . Энергия потока составит 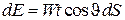, величина импульса . Согласно закону сохранения импульса можно рассчитать элементарные силы и , возникающие вследствие отражения и поглощения света соответственно:

(13)

Зная суммарную силу светового давления 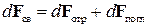, действующую на элементарную площадку 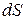, можно путем интегрирования по всей освещенной поверхности космического аппарата 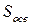рассчитать общую силу , действующую на аппарат, а также момент 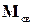относительно его центра масс:

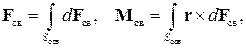
(14)

где 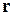– радиус-вектор элементарной площадки 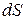относительно центра масс космического аппарата.