Изолированные особые точки. Классификация изолированных особых точек с помощью ряда Лорана. Классификация бесконечно удаленной точки с помощью ряда Лорана.
Важное место в изучении и применении теории функций комплексного переменного занимает исследование их поведения в особых точках, где нарушается аналитичность функции. В частности, это точки, где функция не определена.
Исследование функции в особой точке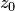 
определяется поведением ее в окрестности этой точки, т.е. исследованием 
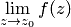. Имеют место три возможности:
а) 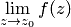не существует;
б) 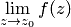существует и равен конечному числу;
в) 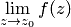равен бесконечности.
Исследование пределов функции в комплексной области — задача более сложная, чем в действительной области, так как, согласно определению, переменная 
стремится к 
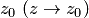по любому направлению. Вычисление пределов в точках аналитичности не представляет интереса, так как в этих случаях 
.
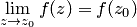Будем рассматривать 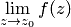, где 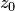— особая точка.
В зависимости от трех случаев поведения функции в особой точке, особые точки функций делят на три типа — производится классификация особых точек. В качестве определения типа особых точек можно выбрать либо поведение функции в особой точке, либо вид ряда Лорана. Выберем первый подход.
Утв 1: Изолированная особая точка 
функции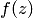 
называется:
– устранимой особой точкой, если 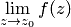существует и конечен
– полюсом, если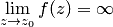 
– существенно особой точкой, если 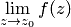не существует
вид ряда Лорана в окрестности особой точки зависит от типа особой точки и потому задача исследования функции в особой точке может быть сведена к исследованию соответствующего ряда Лорана.
1. Для того чтобы особая точка функции была ее устранимой особой точкой, необходимо и достаточно, чтобы в разложении функции в ряд Лорана в окрестности этой точки отсутствовала главная часть. Это означает, что если 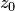— устранимая особая точка, то ряд Лорана функции 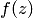имеет вид
|
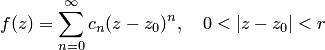
для 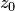— конечной точки 
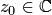, и для 
:
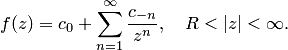
2. Для того чтобы особая точка функции была полюсом, необходимо и достаточно, чтобы главная часть ряда Лорана функции в окрестности этой точки содержала конечное число членов. Ряд Лорана функции 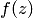в случае 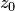полюса имеет вид
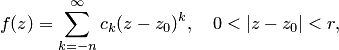
если 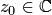, и если , то:
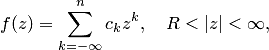
3. Для того чтобы особая точка функции была ее существенно особой точкой, необходимо и достаточно, чтобы главная часть ряда Лорана функции в окрестности этой точки содержала бесконечное число членов. Ряд Лорана функции 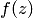в случае 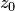— существенно особой точки имеет вид
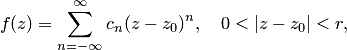
если 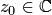, и если , то:
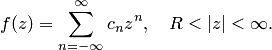
Правила определения порядка полюса в конечной точке:
1. Для того чтобы точка 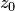была полюсом порядка 
функции 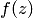, необходимо и достаточно, чтобы ее можно было записать в виде
|
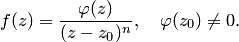
2. Для того чтобы точка 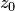была полюсом порядка функции 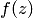, необходимо и достаточно, чтобы она была нулем порядка функции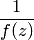 
(связь нулей с полюсами).
3. Если точка 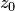является нулем порядка 
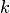функции 
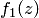и нулем порядка 
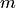функции 
, то она — полюс порядка 
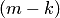для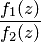 
.
Определение порядка полюса в бесконечно удаленной точке
Рассмотрим бесконечно удаленную точку. Тип особой точки можно определить, вычисляя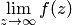 
или раскладывая функцию в ряд Лорана. Можно свести задачу к исследованию конечной точки 
.
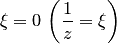Практически удобное правило определения порядка полюса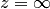 
можно получить, используя утв(1) и правила определения порядка полюса в конечной точке. Действительно, пусть 
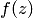для функции , тогда 
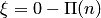для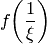 
и можно записать 
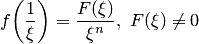Поэтому, обозначив 
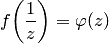, для 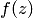получим
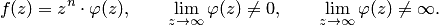
Представление функции в таком виде является необходимым и достаточным условием полюса порядка функции 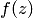в точке .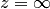